Decision Diagrams for Optimization

News

The 2018 INFORMS Annual meeting again featured several presentations related to decision diagrams.
The first Symposium on Decision Diagrams for Optimization took place at Carnegie Mellon University, October 19-20, 2018.
Slides and videos of the tutorial ``Decision diagrams for Discrete Optimization, Constraint programming, and Integer Programming'' at the 2018 Toulouse Master Class in Hybrid Methods for Combinatorial/Mixed Optimization are now available: Slides, Video part 1, Video part 2.
More tutorials and videos can be found under Presentations below.
Our book Decision Diagrams for Optimization has been published by Springer.
We have added the source code for several projects, including multi-objective optimization, disjunctive scheduling and routing, and Lagrangian bounds from MDDs. These can be found under Publications and software.

Overview

In this research project we utilize decision diagrams to represent discrete optimization problems. Decision diagrams provide a compact representation of the solution set of a given problem, although the size may grow exponentially large. We have therefore developed approximate decision diagrams that have a fixed (polynomial) limit on their size.

As an example, consider the following set covering problem on six binary variables:

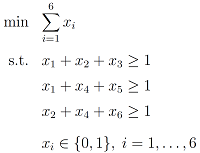
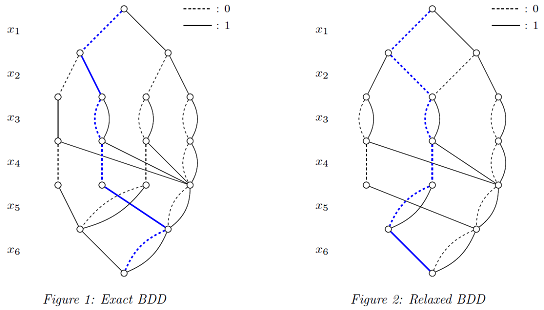
Figure 1 below depicts an exact binary decision diagram (BDD), representing all solutions to the problem. A shortest path, indicated in blue, represents an optimal solution with objective value 2. This exact BDD has `width' 4, where width stands for the maximum number of nodes in any layer. By imposing a limited maximum width we obtain a relaxed BDD. Figure 2 depicts a relaxed binary decision diagram with maximum width 3. It represents all solutions as well as non-solutions. The shortest path in the relaxed BDD is 1, which serves as a lower bound to the problem.

We have successfully applied decision diagrams in the context of

Discrete Optimization: Limited-width decision diagrams can be deployed as relaxations to provide bounds on the objective, and as restrictions to provide feasible solutions. They can naturally be applied in concert to provide an exact solver similar to traditional branch and bound methods.
Constraint Programming: By propagating approximate decision diagrams instead of the traditional variable domains more information can be communicated between the constraints of the problem. This can lead to earlier detection of inconsistencies, smaller search trees, and faster solution times.
Constraint-Based Scheduling: In addition to improved constraint propagation, decision diagrams can be used to reason more effectively on the objective in the context of scheduling. This can speed up existing state-of-the-art solvers by orders of magnitude, for example for disjunctive scheduling with sequence-dependent setup times.
Dynamic Programming: Decision diagrams are closely related to dynamic programming, but provide a more general framework.

People

Faculty at Carnegie Mellon University:

Current and former PhD students:

Sam Hoda (graduated 2010)
David Bergman (graduated 2013)
Andre Cire (graduated 2014)
Brian Kell (graduated 2015)
Marla Slusky (graduated 2015)
Christian Tjandraatmadja (graduated 2018)
Amin Hosseininassab

Current and former postdoctoral researchers:

Joris Kinable (postdoctoral researcher; Eindhoven University per 2017)
Danial Davarnia (postdoctoral researcher; Iowa State University per 2018)

Awards and Honors

Andre Cire received the 2016 Doctoral Research Award from the Association for Constraint Programming for his dissertation "Decision Diagrams for Optimization" at the 2016 annual conference on Principles and Practice of Constraint Programming.
(Picture by Helmut Simonis)
Christian Tjandraatmadja received an honorable mention at the 2015 Mixed Integer Programming Workshop for his poster "Polar Cuts from Relaxed Decision Diagrams".
Andre Cire received the 2014 INFORMS Computing Society Student Paper Award for his paper "Multivalued Decision Diagrams for Sequencing Problems, Operations Research 61(6): 1411-1428, 2013" (joint work with W.-J. van Hoeve).
David Bergman received the 2014 Doctoral Research Award from the Association for Constraint Programming for his dissertation "New Techniques for Discrete Optimization" at the 2014 annual conference on Principles and Practice of Constraint Programming.

Publications and Software

The documents provided on this page are preprints. The copyright for the published documents rests with the author(s) and the journals or conferences where they were published. Where applicable, the source code and benchmark instances are provided. The software can be freely used but comes with no warranty.

Q. Cappart, E. Goutierre, D. Bergman, and L.-M. Rousseau. Improving Optimization Bounds using Machine Learning: Decision Diagrams meet Deep Reinforcement Learning. In Proceedings of AAAI, 2019.

A. Hosseininasab, W.-J. van Hoeve, and A. A. Cire. Constraint-based Sequential Pattern Mining with Decision Diagrams. In Proceedings of AAAI, 2019.

C. Tjandraatmadja. Decision Diagram Relaxations for Integer Programming. PhD thesis, Carnegie Mellon University, 2018.

D. Davarnia and W.-J. van Hoeve. Outer Approximation for Integer Nonlinear Programs via Decision Diagrams. Submitted.

C. Tjandraatmadja and W.-J. van Hoeve. Target Cuts from Relaxed Decision Diagrams. INFORMS Journal on Computing, to appear. (Source code)

D. Bergman and A. A. Cire. Discrete Nonlinear Optimization by State-Space Decompositions. Management Science 64(10):4700-4720, 2017.

J. N. Hooker Job sequencing bounds from decision diagrams, In Proceedings of CP, LNCS 10416, 565-578, 2017.

J. Kinable, A. A. Cire, and W.-J. van Hoeve. Hybrid optimization methods for time-dependent sequencing problems. European Journal of Operational Research 259(3):887-897, 2017.

D. Bergman and A. A. Cire. On Finding the Optimal BDD Relaxation In Proceedings of CPAIOR, LNCS 10335, pp 41-50, 2017.

D. Bergman, A. A. Cire, W.-J. van Hoeve, and J. N. Hooker. Decision Diagrams for Optimization. Springer, 2016.

D. Bergman and A. A. Cire. Theoretical insights and algorithmic tools for decision diagram-based optimization. Constraints, 21(4):533-556, 2016.

D. Bergman, A. A. Cire, W.-J. van Hoeve, and J. N. Hooker. Discrete Optimization with Decision Diagrams. INFORMS Journal on Computing 28(1):47-66, 2016.

D. Bergman and A. A. Cire. Multiobjective Optimization by Decision Diagrams. In Proceedings of CP, LNCS 9892, pp 86-95, 2016.

Source code: multiobjective_cp2016.tar.gz

D. Bergman and A. A. Cire. Decomposition Based on Decision Diagrams. In Proceedings of CPAIOR, LNCS 9676, pp 45-54, 2016.

D. Bergman, A. A. Cire, and W.-J. van Hoeve. Improved Constraint Propagation via Lagrangian Decomposition. In Proceedings of CP, LNCS 9255, pp 30-38, 2015.

Source code: mddCP-Lagrangian.tar.gz
Remarks: For the search type, we typically use "Default search with DFS" (type 5) which works much better for the MDDs. Also, this version uses a simple algorithm to compute the Lagrangian multipliers using cutting planes; other experiments have shown that the Bundle method can be much faster.

D. Bergman, A. A. Cire, and W.-J. van Hoeve. Lagrangian Bounds from Decision Diagrams. Constraints 20(3): 346-361, 2015.

B. Kell, A. Sabharwal, and W.-J. van Hoeve. BDD-Guided Clause Generation. In Proceedings of CPAIOR, LNCS 9075, pp. 215-230, 2015.

A. A. Cire. Decision Diagrams for Optimization. PhD thesis, Carnegie Mellon University, 2014.

D. Bergman, A. A. Cire, and W.-J. van Hoeve. MDD Propagation for Sequence Constraints. JAIR, Volume 50, pages 697-722, 2014.

D. Bergman, A. A. Cire, W.-J. van Hoeve, and T. Yunes. BDD-Based Heuristics for Binary Optimization. Journal of Heuristics 20(2): 211-234, 2014.

D. Bergman, A. A. Cire, A. Sabharwal, H. Samulowitz, V. Saraswat, and W.-J. van Hoeve. Parallel Combinatorial Optimization with Decision Diagrams. In Proceedings of CPAIOR, LNCS 8451, pp. 351-367. Springer, 2014.

Source code: DDX10.zip (requires the X10 software for parallelization)

A. A. Cire and J. N. Hooker. The Separation Problem for Binary Decision Diagrams. In Proceedings of the International Symposium on Artificial Intelligence and Mathematics (ISAIM), 2014.

A. A. Cire and W.-J. van Hoeve. Multivalued Decision Diagrams for Sequencing Problems. Operations Research 61(6): 1411-1428, 2013.

Source code: mddCP-OR.tar.gz
Remark: This updated version (9/15/2016) is compatible with IBM ILOG CPO Optimizer 12.6.

D. Bergman, A. A. Cire, W.-J. van Hoeve, and J. N. Hooker. Optimization Bounds from Binary Decision Diagrams. INFORMS Journal on Computing, to appear.

Source code (C++): opt_bounds_bdd-src.tar.gz
Benchmark instances: opt_bounds_bdd-instances.tar.gz

D. Bergman. New Techniques for Discrete Optimization. PhD thesis, Carnegie Mellon University, 2013.

J. N. Hooker. Decision Diagrams and Dynamic Programming. In Proceedings of CPAIOR. LNCS 7874, pp. 94-110. Springer, 2013.

B. Kell and W.-J. van Hoeve. An MDD Approach to Multidimensional Bin Packing. In Proceedings of CPAIOR, LNCS 7874, pp. 128-143. Springer, 2013.

Benchmark instances: 6-18-6-instances.txt (6 dimensions, 18 items, 6 bins. The instances are named 6-18-6-β_n, where β is the percentage bin slack and n is a sequential number to distinguish instances with identical parameters.)

A. A. Cire and W.-J. van Hoeve. MDD Propagation for Disjunctive Scheduling. In Proceedings of ICAPS, pp. 11-19. AAAI Press, 2012.

D. Bergman, A.A. Cire, W.-J. van Hoeve, and J.N. Hooker. Variable Ordering for the Application of BDDs to the Maximum Independent Set Problem. In Proceedings of CPAIOR. LNCS 7298, pp. 34-49. Springer, 2012.

D. Bergman, W.-J. van Hoeve, and J. N. Hooker. Manipulating MDD Relaxations for Combinatorial Optimization. In Proceedings of CPAIOR. LNCS 6697, pp. 20-35. Springer, 2011.

S. Hoda. Essays on Equilibrium Computation, MDD-based Constraint Programming and Scheduling. PhD thesis, Carnegie Mellon University, 2010.

S. Hoda, W.-J. van Hoeve, and J. N. Hooker. A Systematic Approach to MDD-Based Constraint Programming. In Proceedings of CP. LNCS 6308, pp. 266-280. Springer, 2010.

T. Hadzic, J. N. Hooker, B. O'Sullivan, and P. Tiedemann. Approximate compilation of constraints into multivalued decision diagrams. In Proceedings of CP. LNCS 5202, pp. 448-462. Springer, 2008.

T. Hadzic, J. N. Hooker, and P. Tiedemann. Propagating separable equalities in an MDD store. In Proceedings of CPAIOR. LNCS 5015, pp. 318-322. Springer, 2008.

H. R. Andersen, T. Hadzic, J. N. Hooker, and P. Tiedemann. A constraint store based on multivalued decision diagrams. In Proceedings of CP. LNCS 4741, pp. 118-132. Springer, 2008.

Tarik Hadzic and J. N. Hooker. Cost-bounded binary decision diagrams for 0-1 programming. In Proceedings of CPAIOR. LNCS 4510, pp. 84-98. Springer, 2007.

Tarik Hadzic and J. N. Hooker. Postoptimality analysis for integer programming using binary decision diagrams. December 2007, revised April 2008 (not submitted).

Presentations

Plenary Talks and Tutorials

W.-J. van Hoeve. Decision Diagrams for Discrete Optimization, Constraint Programming, and Integer Programming. Master Class in Hybrid Methods for Combinatorial/Mixed Optimization. June 4-5, 2018, Toulouse, France. Slides, Video part 1, Video part 2.

J. N. Hooker, Decision Diagrams for Discrete Optimization. Tutorial at the International Conference on Automated Planning and Scheduling (ICAPS), 2016.
Video available on YouTube.

W.-J. van Hoeve, Decision Diagrams for Sequencing and Scheduling. Tutorial at the International Conference on Automated Planning and Scheduling (ICAPS), 2016.
Video available on YouTube.

W.-J. van Hoeve, Decision Diagram based Constraint Programming, ACP Summer School, 2015. part 1, part 2, part 3.

W.-J. van Hoeve, Decision Diagrams for Optimization and Scheduling. MAPSP, 2015.

A. A. Cire, Decision Diagrams for Optimization, MIP, 2015.

W.-J. van Hoeve, Decision Diagrams for Discrete Optimization. Tutorial Forum, Twenty-Seventh AAAI Conference, 2013.
Video's: Part 1, Part 2, Part 3
Solutions to the exercises can also be downloaded.

W.-J. van Hoeve, Constraint Programming with Decision Diagrams. International Conference on Principles and Practice of Constraint Programming (CP), 2012.

W.-J. van Hoeve, Decision Diagrams for Discrete Optimization, MIP, 2011.

J. N. Hooker, Multivalued decision diagrams and what they can do for you. Keynote talk, CP Workshop on Constraint Reasoning and Graphical Structures, 2010.

Acknowledgements

This research is supported by NSF grant CMMI 1130012, AFOSR grant FA9550-11-1-0180, and a Google Research Award.