Example (strtxmpl4.sas): creating start values to fit a trajectory model with time-varying covariates (TCOV).
The purpose of this example is to create starting values to fit a trajectory model with time-varying covariates. To simplify the example, we'll start assuming we've established the appropriate number of groups and order for the trajectory model.
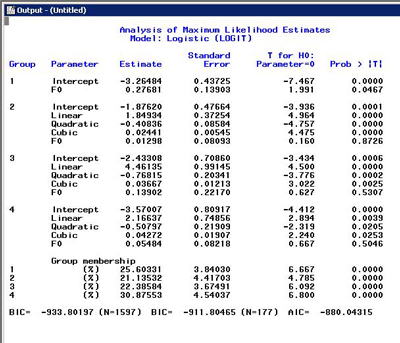
Step 1: Fit the trajectory model without the time-varying covariate.
LOGIT model, intercept-only and cubic trajectories.
Model results.
Log 1: LOGIT model ending values.

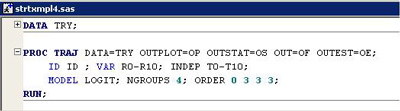
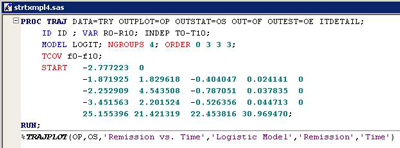
The starting values option is used to add the initial model. The ending values for the initial model are copied from the log. Since this example does not use risk factors, the first set of ending values are used. The following shows the values pasted into the program with zeros added where the TCOV estimates go as seen below.
Program
2: Starting values to fit model adding a TCOV.
|
|
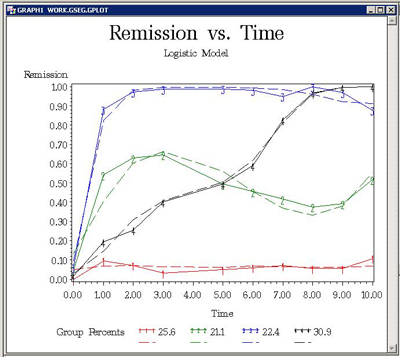
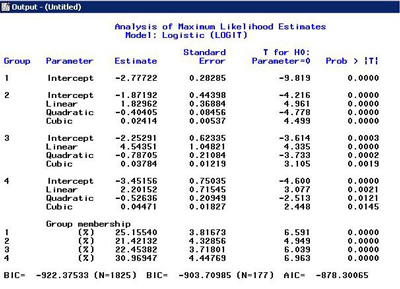
Output 2: Four-group model with TCOV and Graph 1: Average data (solid line) and mean (dashed line) trajectories.