- Given your open loop step response, calculate the gain and time constant (K and
 ).
). - Write the open loop transfer function of the amp-motor-tach system.
- Show that the bandwidth frequency occurs at
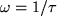 . The output magnitude is equal to the
magnitude of the transfer function with
. The output magnitude is equal to the
magnitude of the transfer function with 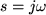 . Set this to -3dB and solve for
. Set this to -3dB and solve for 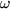 .
. - Given your transfer function obtained earlier, calculate the expected bandwidth frequency. How does this compare to the frequency obtained experimentally.
- Compare this frequency to the bandwidth obtained from the signal analyzer. Why might they be different? Why might the amplitude of the spectrum analyzer's output be different than that obtained by hand? (hint - consider friction).
How does the open loop system respond to a disturbance? Why is this not surprising?
- Write the closed-loop transfer function. Solve for the closed loop gain,
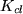 , and time constant,
, and time constant, 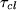 , in terms of the open
loop parameters and the controller gain, Kc. Do not substitute in numbers yet.
, in terms of the open
loop parameters and the controller gain, Kc. Do not substitute in numbers yet. - What happens to
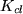 and
and 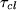 as Kc is
increased?
as Kc is
increased? - What happens to the closed-loop pole as Kc is increased?
- Calculate the value of Kc that will make
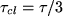 symbolically.
symbolically. - Plug in the numbers and show your calculations for the resistance value of the potentiometer.
- Calculate the actual
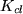 and
and 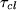 from your step response. Compare this to what is expected. Why might they be different?
from your step response. Compare this to what is expected. Why might they be different? - Calculate the transfer function from the input to the control signal (the signal between the controller and the amplifier) given your open-loop transfer function.
- For the step input given to the system, find the control signal as a function of time.
- Compare the observed control signal to the expected control signal. Look at the steady-state value, the shape of the response, and the size of the peaks.
- Why might you want to use a very large gain in this controller? Why can't you use an arbitrarily large gain? Think in terms of the control signal and the capabilities of the amplifier.
- What bandwidth would you expect in closed loop, given your theoretical closed loop
transfer function? Also calculate it in terms
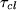 . Compare these values to the observed
bandwidth. Why might they be different.
. Compare these values to the observed
bandwidth. Why might they be different. - Compare the bandwidth obtained from the signal analyzer to these values. Explain any differences.
- Why does bandwidth give a good indication of the performance of the control system?
- Compare what you observed in closed-loop to what you observed in open-loop.
- Physically, how does the system respond to a disturbance? Explain what the controller does in response to the disturbance.
- For closed loop, assuming the disturbance adds in at the control signal, calculate the transfer function from the disturbance to the output in terms of Kc. What happens to the steady-state response as Kc is increased? What does this say about Kc?
- Calculate the closed-loop transfer function in positive feedback.
- Compute the pole of this transfer function. What does this say about the final value and the stability?
- Compute the response to an impulse input as a function of time. compare this to what you observed and plotted.
- Will all systems be unstable in positive feedback?
- Will any systems be unstable in negative feedback?