SEMITIP V6, Uni2, Example 5: comparison with inverse solution, for undoped semiconductor
Click here for input/output files, main program source code, and PotInt.f routine, for Example 4
This example illustrates the validation of our band bending computation, as described in
R. M. Feenstra, S. Gaan, G. Meyer, and K. H. Rieder, Phys. Rev. B 71, 125316 (2005).
We compute the band bending computation for an undoped semiconductor, assuming dielectric constant of 16.3 (as appropriate to Ge) and a band gap of 2 eV. A sample voltage of +3 V is applied. We then take that solution and, using the surface charge on the tip, recomputate the boundary condition for the potential, i.e. +3 V on the probe tip. The figure below shows results for the potential on the apex of the tip minus the potential on the point on the surface opposite the tip apex. With a potential at that latter point of about 0.87 eV, this difference is about 2.13 eV. The plot shows this difference as a function of the number of grid points (with the same number used in the radial direction, the direction into the semiconductor, and in the vacuum).
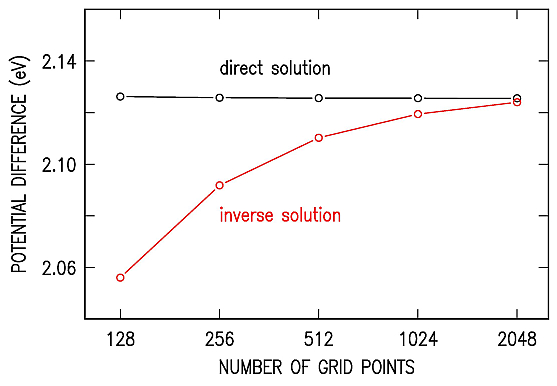We see that the direct solution for the potential converges very well even for 128 grid points (a typical value for the final scaling step of the computation). More grid points are needed for the inverse solution to converge to this direct solution, but nevertheless that convergence does indeed occur for a sufficiently fine grid. This agreement does provide one important validation test for the solution of the electrostatic potential, although it does not prove that the solution is completely correct. Indeed, with version 4 or 5 of SEMITIP, a similar agreement was found between the direct and inverse solutions, for the same parameters as used here, but in that case the band bending was only 0.50 eV (potential difference of 2.50 eV) rather than the present 0.87 eV (difference of 2.13 eV). In that previous case an approximation was used in computing the derivatives for our variable-spaced grid (see discussion of
Computation of Derivatives for Variable Grid Spacing), and apparently the errors from that approximation affected both the direct solution and the inverse solution nearly equally. But nevertheless, the agreement found in the figure above does provide an important, if not definitive, validation for our solution for the electrostatic potential.