
Dionisio de Niz
Software Engineering Institute | Carnegie Mellon University
Site menu:
Projects
This page only presents some of the projects I work on.Sample CPS
It is always useful to start with a simple example that exhibits the properties that we want to focus on. On this airbag video:
it is possible to see two airbags: one that inflates at the right time and another that deploys late. This represents the character of a Cyber-Physical System that needs to execute the steps correctly (infate the airbag) and execute them at the proper time in sync with the physical process (the driver traveling towards the steering wheel in a crash).
Below are some of the projects we work on.
- Zero-Slack Scheduling
- Real-Time Multicore Scheduling
- Symbolic Assurance Refinement
- Mixed-Trust Computing for CPS
Zero-Slack Scheduling
Zero-Slack Scheduling is a scheduling framework for real-time mixed-criticality systems. Specifically, it targets systems where the utilization-based scheduling priorities are not aligned with the criticality of the tasks. With this framework we implemented a family of schedulers, resource allocation protocols, and synchronization protocols to support the scheduling of mixed-criticality systems.
Mixed-Criticality Scheduling and Safety Standards
Safety standards like the DO-178B for avionics and the ISO 26262 in automotive include safety levels that map to criticality levels. For a discussion of the use of Mixed-Criticality scheduling in automotive systems with AutoSAR and ISO 26262 please look at the paper: Applying the AUTOSAR timing protection to build safe and efficient ISO 26262 mixed-criticality systems
Zero-Slack QRAM
Zero-Slack Q-RAM combines ZS-RM and Q-RAM to enable overbooking (cycles allocated to more than one task) not only between tasks of different criticality but also to task with different utility to the mission of the system.
We implemented three version of the ZS-QRAM scheduler: a modification to the Linux/RK kernel (and kernel module), an independent kernel module implementation, and a daemon-based implementation.
We developed a number of experiments to showcase the effects of the scheduler in a drone mission. In particular, first we demonstrate how the wrong scheduling can actually crash a drone. This is shown in this video.
Secondly, we showcase how in a full mission ZS-QRAM not only preserve the saftey of the flight but also maximizes the utility of the mission. In particular, the demo shows a surveillance mission where a video-streaming task and an object recognition tasks are dynamically adjusted according to their utility to the mission. This video shows this case.
Download Scheduler Implementations
To access both the kernel and kernel module implementations, please go to our Drone RK site.Multiple variations of the ZSRM/ZSQRAM scheduler and analysis tools had been developed. Some of these implementation can be accessed by selecting the appropriate tab below.
A library implementation for VxWorks can be downloaded from the ECE WISE Lab website.
Please read the agreement below. By clicking 'I accept' at the end of this agreement, you are declaring that you agree with the terms of this licensing agreement.
Copyright (c) 2012 Carnegie Mellon University.
All Rights Reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
1. Redistributions of source code must retain the above copyright notice, this list of conditions and the following acknowledgments and disclaimers.
2. Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
3. The names Carnegie Mellon University, "SEI and/or Software Engineering Institute" shall not be used to endorse or promote products derived from this software without prior written permission. For written permission, please contact permission@sei.cmu.edu.
4. Products derived from this software may not be called "SEI" nor may "SEI" appear in their names without prior written permission of permission@sei.cmu.edu.
5. Redistributions of any form whatsoever must retain the following acknowledgment:
This material is based upon work funded and supported by the Department of Defense under Contract No. FA8721-05-C-0003 with Carnegie Mellon University for the operation of the Software Engineering Institute, a federally funded research and development center.
Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the United States Department of Defense.
NO WARRANTY. THIS CARNEGIE MELLON UNIVERSITY AND SOFTWARE ENGINEERING INSTITUTE MATERIAL IS FURNISHED ON AN AS-IS BASIS. CARNEGIE MELLON UNIVERSITY MAKES NO WARRANTIES OF ANY KIND, EITHER EXPRESSED OR IMPLIED, AS TO ANY MATTER INCLUDING, BUT NOT LIMITED TO, WARRANTY OF FITNESS FOR PURPOSE OR MERCHANTABILITY, EXCLUSIVITY, OR RESULTS OBTAINED FROM USE OF THE MATERIAL. CARNEGIE MELLON UNIVERSITY DOES NOT MAKE ANY WARRANTY OF ANY KIND WITH RESPECT TO FREEDOM FROM PATENT, TRADEMARK, OR COPYRIGHT INFRINGEMENT.
This material has been approved for public release and unlimited distribution.
Carnegie Mellon is registered in the U.S. Patent and Trademark Office by Carnegie Mellon University.
DM-0000105
I Accept
Copyright (c) 2014 Carnegie Mellon University.
All Rights Reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
1. Redistributions of source code must retain the above copyright notice, this list of conditions and the following acknowledgments and disclaimers.
2. Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following acknowledgments and disclaimers in the documentation and/or other materials provided with the distribution.
3. Products derived from this software may not include “Carnegie Mellon University,” "SEI” and/or “Software Engineering Institute" in the name of such derived product, nor shall “Carnegie Mellon University,” "SEI” and/or “Software Engineering Institute" be used to endorse or promote products derived from this software without prior written permission. For written permission, please contact permission@sei.cmu.edu.
ACKNOWLEDMENTS AND DISCLAIMERS:
Copyright 2014 Carnegie Mellon University
This material is based upon work funded and supported by the Department of Defense under Contract No. FA8721-05-C-0003 with Carnegie Mellon University for the operation of the Software Engineering Institute, a federally funded research and development center.
Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the United States Department of Defense.
NO WARRANTY. THIS CARNEGIE MELLON UNIVERSITY AND SOFTWARE ENGINEERING INSTITUTE MATERIAL IS FURNISHED ON AN “AS-IS” BASIS. CARNEGIE MELLON UNIVERSITY MAKES NO WARRANTIES OF ANY KIND, EITHER EXPRESSED OR IMPLIED, AS TO ANY MATTER INCLUDING, BUT NOT LIMITED TO, WARRANTY OF FITNESS FOR PURPOSE OR MERCHANTABILITY, EXCLUSIVITY, OR RESULTS OBTAINED FROM USE OF THE MATERIAL. CARNEGIE MELLON UNIVERSITY DOES NOT MAKE ANY WARRANTY OF ANY KIND WITH RESPECT TO FREEDOM FROM PATENT, TRADEMARK, OR COPYRIGHT INFRINGEMENT.
This material has been approved for public release and unlimited distribution.
Carnegie Mellon® is registered in the U.S. Patent and Trademark Office by Carnegie Mellon University.
DM-0000891
I Accept
Please read the agreement below. By clicking 'I accept' at the end of this agreement, you are declaring that you agree with the terms of this licensing agreement.
Copyright (c) 2014 Carnegie Mellon University.
All Rights Reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
1. Redistributions of source code must retain the above copyright notice, this list of conditions and the following acknowledgments and disclaimers.
2. Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following acknowledgments and disclaimers in the documentation and/or other materials provided with the distribution.
3. Products derived from this software may not include “Carnegie Mellon University,” "SEI” and/or “Software Engineering Institute" in the name of such derived product, nor shall “Carnegie Mellon University,” "SEI” and/or “Software Engineering Institute" be used to endorse or promote products derived from this software without prior written permission. For written permission, please contact permission@sei.cmu.edu.
ACKNOWLEDMENTS AND DISCLAIMERS:
Copyright 2014 Carnegie Mellon University
This material is based upon work funded and supported by the Department of Defense under Contract No. FA8721-05-C-0003 with Carnegie Mellon University for the operation of the Software Engineering Institute, a federally funded research and development center.
Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the United States Department of Defense.
NO WARRANTY. THIS CARNEGIE MELLON UNIVERSITY AND SOFTWARE ENGINEERING INSTITUTE MATERIAL IS FURNISHED ON AN “AS-IS” BASIS. CARNEGIE MELLON UNIVERSITY MAKES NO WARRANTIES OF ANY KIND, EITHER EXPRESSED OR IMPLIED, AS TO ANY MATTER INCLUDING, BUT NOT LIMITED TO, WARRANTY OF FITNESS FOR PURPOSE OR MERCHANTABILITY, EXCLUSIVITY, OR RESULTS OBTAINED FROM USE OF THE MATERIAL. CARNEGIE MELLON UNIVERSITY DOES NOT MAKE ANY WARRANTY OF ANY KIND WITH RESPECT TO FREEDOM FROM PATENT, TRADEMARK, OR COPYRIGHT INFRINGEMENT.
This material has been approved for public release and unlimited distribution.
Carnegie Mellon® is registered in the U.S. Patent and Trademark Office by Carnegie Mellon University.
DM-0000891
I Accept
Real-Time Multicore Scheduling
Multicore processors are quite different from multi-processors. This is due to the fact that cores within a processor share resources. One of the most critical shared resources is the memory system. This includes both shared cache and shared RAM memory. The effect of the memory interference that one task running on one core in another running on a different core can be really significant. We have seen extreme cases of 12X increases in the execution time due to memory interference (as can be seen in the figure below) and some practitioners have observed 3X. This 3X basically means that in a dual core processor I am better of shutting down a core to avoid a DECREASE in the execution speed.
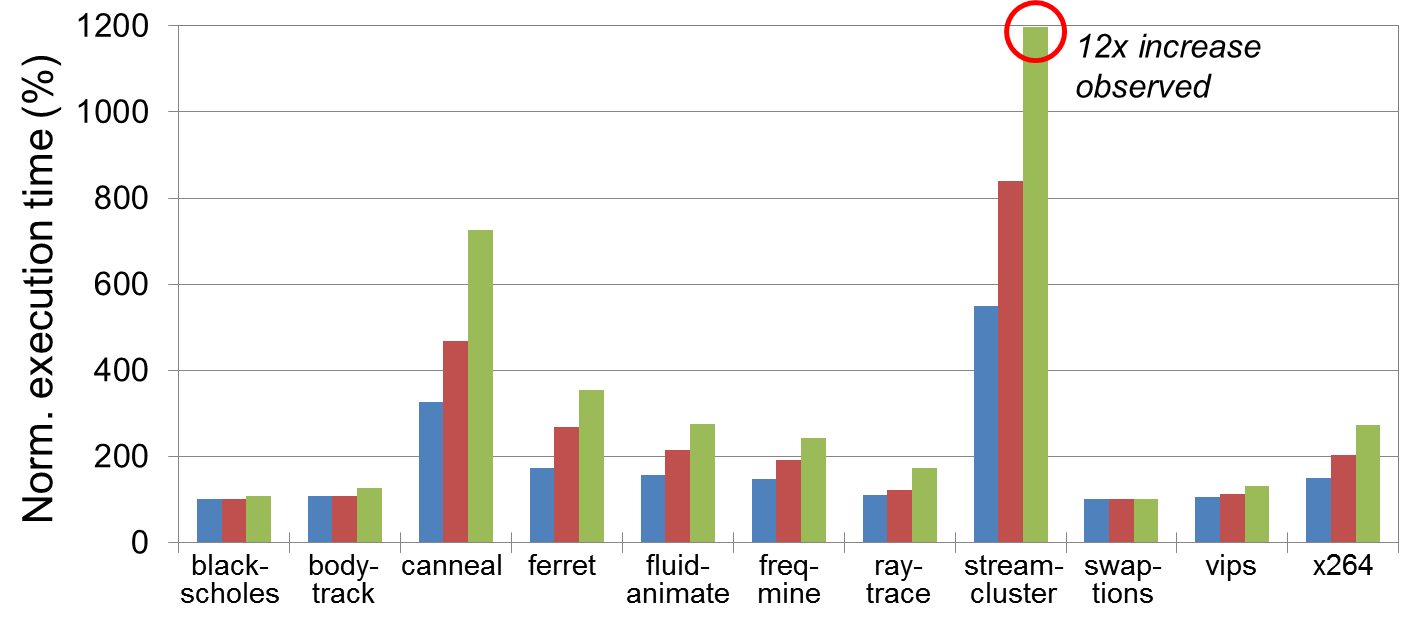
Once you solve the interference problem due to shared resources we need to support new tasks with parallelized jobs that need more than one core to complete before the deadline. New scheduling algorithms are necessary to schedule these tasks and these need to be combined with memory partitions to maximize their utilization and guarantee their time predictability.
At the SEI we have been working with the CMU RTML on the memory by creating partitioning mechanisms to eliminate or reduce this interference along with analysis algorithms to take into account residual effects.
Partitions with Page Coloring
A key mechanism we use is page coloring. Page coloring takes advantage of the virtual memory system that translates virtual memory addresses to physical addresses to assign physical addresses that do not interference with each other to different tasks running on different cores. This mechanism is combined with characteristics of the memory hardware that divide the memory into areas that do not interference with each other. Different mechanisms exist for cache and main memory.
Cache Partitions (Cache coloring)
Cache fast memory that is used in the memory system to load memory blocks that are frequently used. This means that the first time a variable is read by the CPU this variable is loaded in the cache and any following access to the variable is done in the cache at a much faster speed. However, caches are much smaller than main memory and as the program executes it will stop using some variables. The cache system remembers if a variable has not been access frequently and selects its cache block to be replaced by a newly access variable that has no empty room in the cache for it. When a variable from a task in one core replaces the cache block of the variable of another task in another core it creates a delay in the execution of the latter because it needs to go all the way back to memory to access it again.
Most cache hardware divide the cache into sets of cache blocks in what is known as set-associativity. Each set is restricted to be used for certain area of the physical memory and cannot be used by any other. We take advantage of this and ensure that the physical memory used by one tasks in one core belongs to one of these regions while the memory of another task running on a different core belongs to a different one. This is what is known as cache coloring that effectively creates cache partitions.
Memory Bank Partitions (Bank Coloring)
While cache coloring provides a great benefit to reduce the interference across cores, its not enough to solve the problem. Main memory is another source of interference that can be significant. In fact, the experiments shown in the figure above is due to memory interference and not cache interference. Main memory is divided into regions called banks. This banks in turn are organized into rows and columns. Whenever a task running in a core tries to access a memory address in main memory first this address is analyzed to extract three pieces of information (out of specific bits in the memory address): (i) the bank number, (ii) the row number, (iii) the column number. The bank memory is used to select the bank where the memory block is located. Then the memory controller loads the row from that bank into a row buffer within the bank for faster access. Finally the memory block is access in the column indicated by the column number from the row buffer. This can be seen in the figure below.
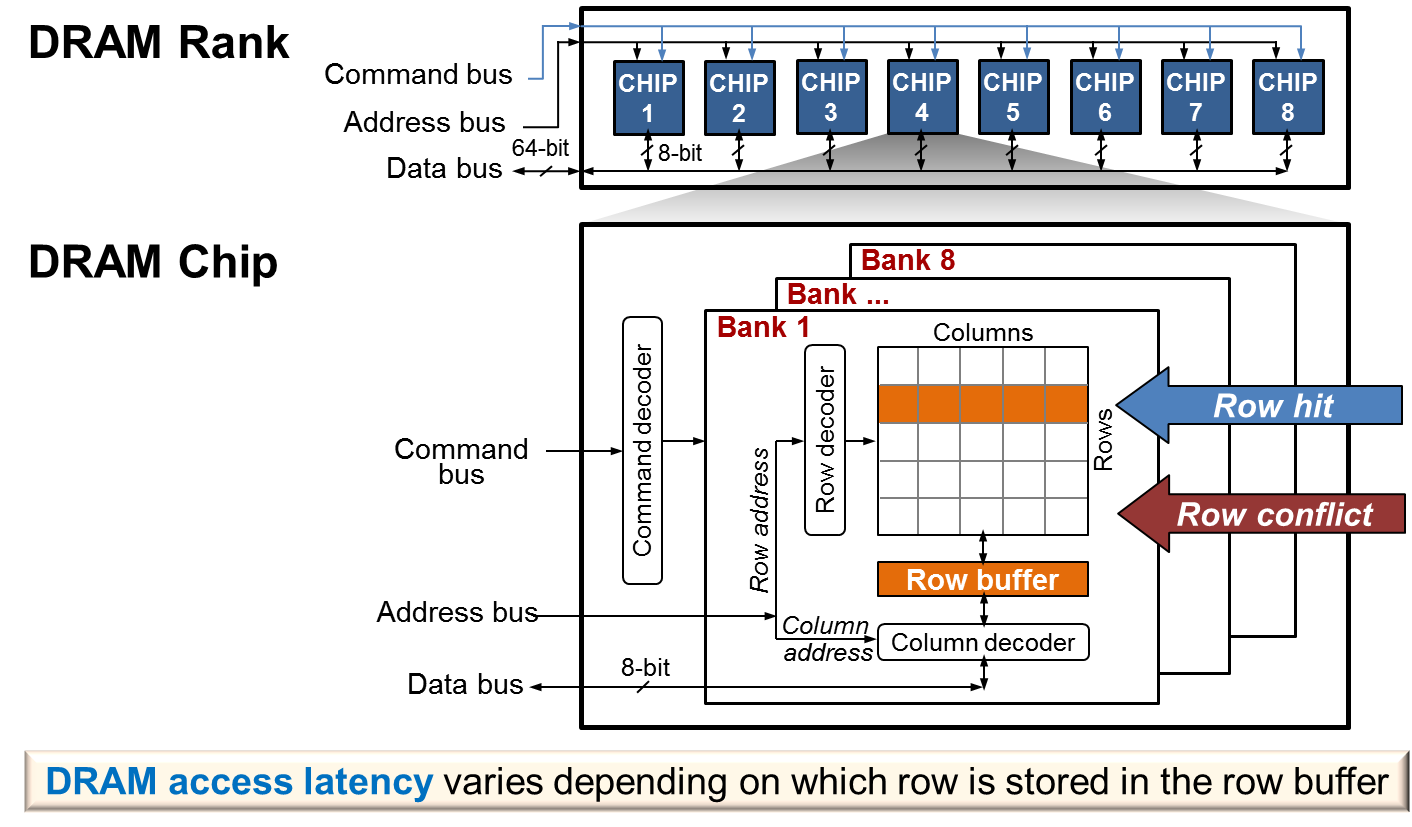
Because the memory controller is optimized to improve the memory accesses per second, it takes advantage of the row buffer and favors the memory accesses that go to the same row. Unfortunately this means that when a task 1 in one core is accessing a row (already loaded in the row buffer) while a task 2 running in another core is trying to access another row in the same bank, the access from task 2 can be move back in the memory access queue by another more recent access from task 1 to the already loaded row multiple times, creating an important delay for task 1.
Memory bank partitions are created by mapping the memory of the different tasks to different memory banks. This way each task can have its own bank and row buffer an no other task will modify that buffer or the queue of memory accesses to this bank.
Combined Cache and Bank Partitions
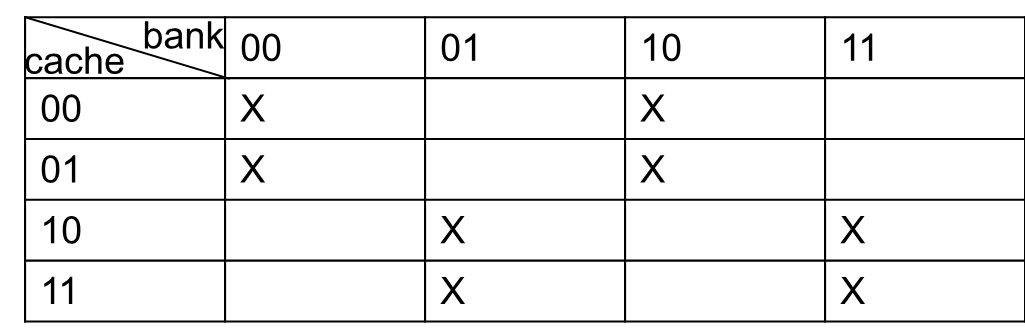
Because caches and memory banking technologies were not developed together, more often than not, their partitions intersect each other. In other words, it is not possible to select a bank color independent from a cache color because the selection of a cache color may limit the number of bank colors available. This is because in some processor architectures, the address bit used to select a bank and the bits used to select a cache set share some elements. To illustrate this issue consider a memory system with four banks and four cache sets. In this case, we need two address bit to select a bank and two bits to select a cache set. If they were independent then we would be able to select four cache colors for each bank color we can select for a total of 16 combinations. This can be seen as a matrix (a color matrix) where rows are cache colors and columns are bank colors. However, if they share one bit then in reality we only have 23=8 colors. This means that in the color matrix some of the cells will not be real. This is shown in the figure below
Coordinated Cache, Bank, and Processor Allocation
We developed a coordinated allocation approach to allocate cache and bank colors along with processor to taks in order to avoid the cache/bank color conflicts and to maximize the effectiveness of the memory partitions taking into account the difference between inter and intra core interference.
We developed memory reservations with cache and memory partitions in the Linux/RK OS.
Limited Number of Partitions
Unfortunately, the number of partitions that is possible to obtain with page coloring is limited. For instance, for an Intel i7 2600 processor it is possible to obtain 32 cache colors and 16 bank colors. Given that, in practice, we may have a larger number of tasks (say 100), these number of partitions may prove insufficient for a real system. As a result, it is important to also enable the sharing of partitions whenever the memory bandwidth requirements of tasks allows it. However, this sharing must be done in a predictable way ensuring that we can guarantee meeting the tasks deadlines. At the same time it is important to avoid pessimistic over-approximations in order not to waste the processor cycles that we were trying to save in ther first place. For this case we developed an analysis algorithm that allows us to verify the timing interference of private and share memory partitions.
Parallelized Tasks Scheduling
Beyond solving the resource sharing problem we also need to enable the execution of parallelized tasks. For this we have developed a global EDF scheduling algorithm for parallelized tasks with staged execution. These tasks generate jobs composed of a set of sequential stages that in turn are composed of a set of parallel segments. This segments are allowed to run in parallel to each other provided that all the segments from the previous stage have completed or the task has arrived for the first segments of the first stage. Our algorithm allows us to verify the schedulability of these tasks with a global EDF scheduler. Beyond EDF, it is possible to use this algorithm with a global fixed priority scheduler with synchronous start, harmonic periods and implicit deadlines, a common configuration used by practitioners.
Please read the agreement below. By clicking 'I accept' at the end of this agreement, you are declaring that you agree with the terms of this licensing agreement.
Copyright 2014 Carnegie Mellon University
This material is based upon work funded and supported by the Department of Defense under Contract No. FA8721-05-C-0003 with Carnegie Mellon University for the operation of the Software Engineering Institute, a federally funded research and development center.
Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the United States Department of Defense.
This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 2 of the License. The GNU General Public License is available at https://www.gnu.org/licenses/gpl-2.0.txt
NO WARRANTY. THIS CARNEGIE MELLON UNIVERSITY AND SOFTWARE ENGINEERING INSTITUTE MATERIAL IS FURNISHED ON AN "AS-IS" BASIS. CARNEGIE MELLON UNIVERSITY MAKES NO WARRANTIES OF ANY KIND, EITHER EXPRESSED OR IMPLIED, AS TO ANY MATTER INCLUDING, BUT NOT LIMITED TO, WARRANTY OF FITNESS FOR PURPOSE OR MERCHANTABILITY, EXCLUSIVITY, OR RESULTS OBTAINED FROM USE OF THE MATERIAL. CARNEGIE MELLON UNIVERSITY DOES NOT MAKE ANY WARRANTY OF ANY KIND WITH RESPECT TO FREEDOM FROM PATENT, TRADEMARK, OR COPYRIGHT INFRINGEMENT.
This material has been approved for public release and unlimited distribution.
Carnegie Mellon(R) is registered in the U.S. Patent and Trademark Office by Carnegie Mellon University.
DM-0001994
I Accept
Symbolic Assurance Refinement
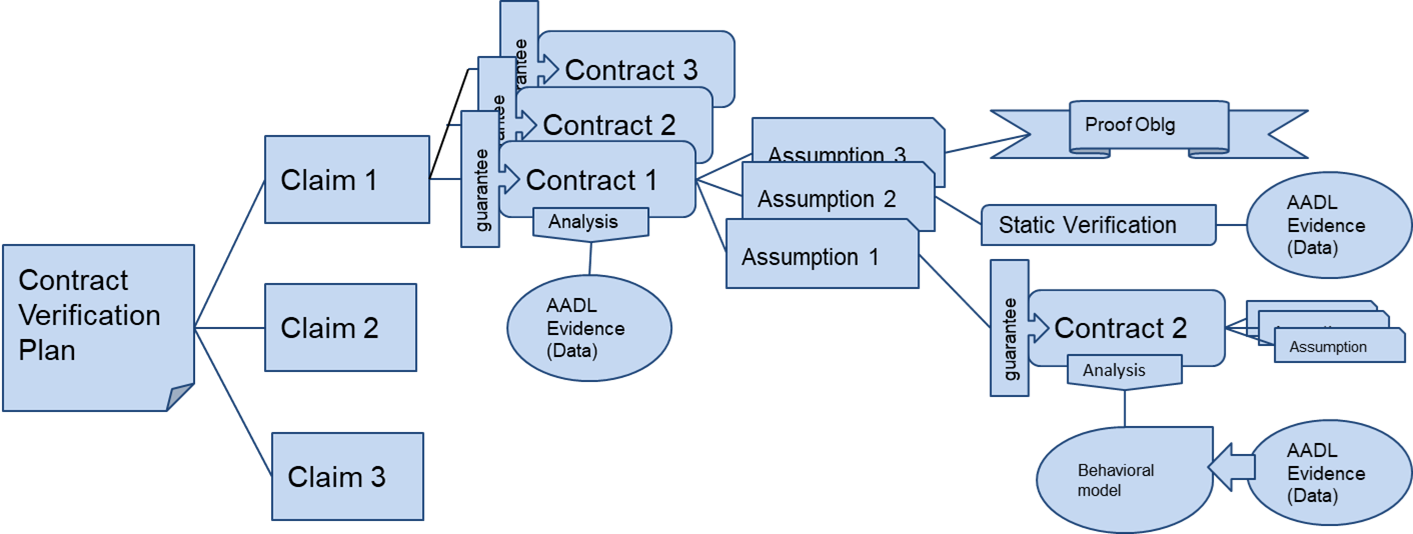
The Symbolic Assurance Refinement creates an argumentation based on verification analysis from different domains (real-time verification, logical verification, control-theoretic verification). For each analysis we create a contract that specifies what are the assumptions of the analysis and what are the guarantees that it provices as shown in the figure below.

The assumptions of the analysis contract can be validated by simple comparisons with the system model if we have the information, with yet another analysis contract if the verification procedure of the property is complex enough, or it can be deferred as a proof obligation.
A Flight Incident Sample Argumentation with SAR
As part of our engagement with the CPS and certification community we created the ASERT workgroup (https://asertw.org) with participation from the FAA, DOT&E, DTVV, NASA, Boeing, LMCO and others. The work in this group is structured as a set of experiments that evaluates the development of technology for automated certification. In the first experiment, named Experiment Zero we model the case of a triple computer failure during the landing of flight CI202 in Taipei in 2020. More specifically, during the landing, the plane bounced of the ground a couple of times creating a channel asynchrony between self-checking pairs. Self checking pairs are function executed in different processors and developed by different teams that calculate the same value. The value calculated by a pair is compared with each other and if they differ by a certain amount, it is assumed that the calculation is incorrect and the system fails over to another replica of this pair. In the plane from the incident there were three replicas and the three failed one after another.
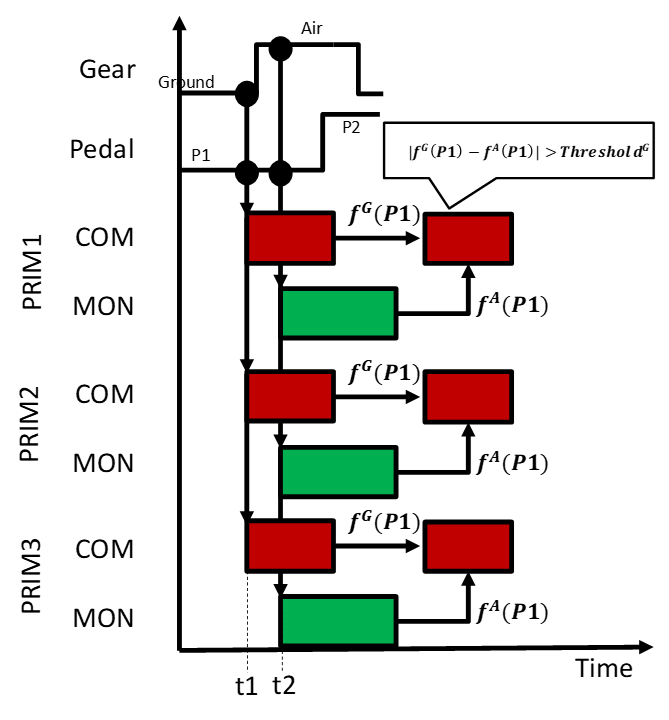
Channel Asynchrony
The failure was explained as a channel asynchrony, were the self-checking pair has two modes of operation: air and ground. In the air the functions calculate the actuation to control the rudder, and in the ground the actuation for the wheels of the aircraft. Unfortunately, the bouncing of the plane made one of the functions of the pair to calculate the actuation of the rudder and the other of the wheels. Hence, the comparison failed and replica failed. This occured in the three computers one after another. A diagram of the channel asynchrony is shown in the following figure.
Verification Plan
We created a verification plan that used real-time scheduling to verify the end-to-end timing requirements, the probabilistic Fault-Tree Analysis to validate the requirements of the availability, and a contract to specify that the maximum sensing (input) jitter between self-checking pair components needed to be zero (we explored other options but only this is presented in the report). The top level verification plan is shown in the following figure.
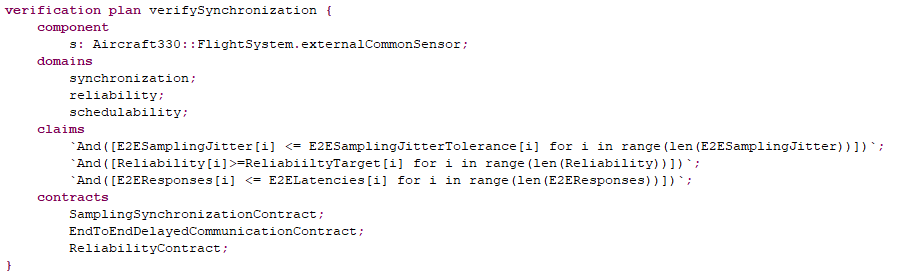
With this plan we verified that if each component in the self-checking pair uses its own sensor and thread to read the sensor then it is not possible to ensure that the input jitter will be zero. Hence, we modify the architecture and used a single sensor and thread per self-checking pair that ensures that both self-checking pair functions received the same sensor readings.
Flight Incident Analysis Video Presentation and Demo
This is a video presentation and demo of the flight incident analysis.
Installing SAR
Please go to the ACPS project website to install the tool and run the demo at: acps-sei.github.ioReferences
1. Dionisio de Niz, Bjorn Andersson, Mark H. Klein, John Lehoczky (Carnegie Mellon University), Hyoseung Kim (University of California, Riverside), George Romanski (Federal Aviation Administration), Jonathan Preston (Lockheed Martin Corporation), Daniel Shapiro (Institute of Defense Analysis), Floyd Fazi (Lockheed Martin Corporation), Douglas Schmidt (Vanderbilt University), David Tate (Institute of Defense Analysis), Gordon Putsche (The Boeing Company), Ronald Koontz (Boeing Company).
Encoding Verification Arguments to Analyze High-Level Design Certification Claims: Experiment Zero (E0).
Technical Report ([ASERT Workgroup](https://asertw.org)).
2. Dionisio de Niz and Lutz Wrage.
Symbolic Refinement for CPS.
ACM SIGAda Ada Letters 43(1):88-93. DOI 10.1145/3631483.3631498. 2023
Mixed-Trust Computing for CPS
Verifying complex Cyber-Physical Systems (CPS) is increasingly important given the push to deploy safety-critcal autonomous features. Unfortunately, traditional verification methods do not scale to the complexity of these systems and do not provide systematic methods to proetct verified properties when not all the components can be verified. To address these challenges in this project we develop a real-time mixed-trust computing famework that combines verification and protection. The framework introduces a new task model, where an application task can have both an untrusted and a trusted part. The untrusted part allows complex computations supported by a full OS with a real-time scheduler running in a VM hosted by a trusted hypervisor (HV). The trusted part is executed by another scheduler within the hypervisor and is thus protected from the untrusted part. If the untrusted part fails to finish by a specified time, the trusted part is activated to preserve safety (e.g. prevent a crash) including its timing guarantees. This framework is the first allowing the use of untrusted components for CPS critical functions while preserving logical and timing guarantees even in the presence of malicious attackers. In this project we implemented the framework based on the XMHF hypervisor and the ZSRM scheduler and developed the schedulability analysis and the coordination protocol between the trusted and untrusted parts.
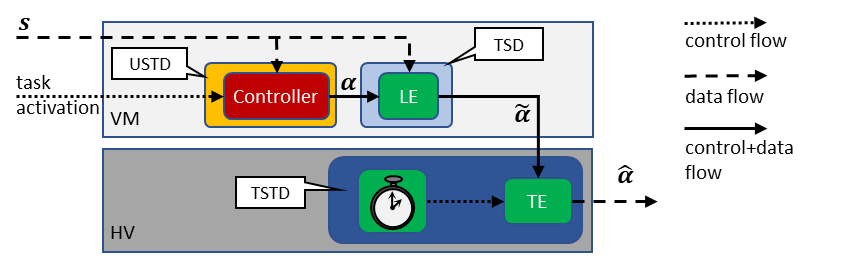
The mixed-trust computation framework is part of our enforcement-based verification where the output of un unverified component is validated by a verified logical enforcer (LE) who validates the safety of this actions. If the LE deems the output unsafe it replaces it with a safe one. Given that the unsafe component can delay the output beyond its deadline (as it executes in a real-time task) the trusted component in the hypervisor (that is also part of the task) executes a safe computation (with a safe output) before the deadline is missed. The untrusted component and the LE are combined into what we call a guesttask (GT) (given that it runs in the guest VM) and the trusted component running in the HV is considered a hypertask (HT). Together the GT and the HV form a mixed-trust task that is scheduled to ensure that their combined execution (with the rules discussed before) do not miss its deadline. The following figure depicts the architecture of the mixed-trust task.
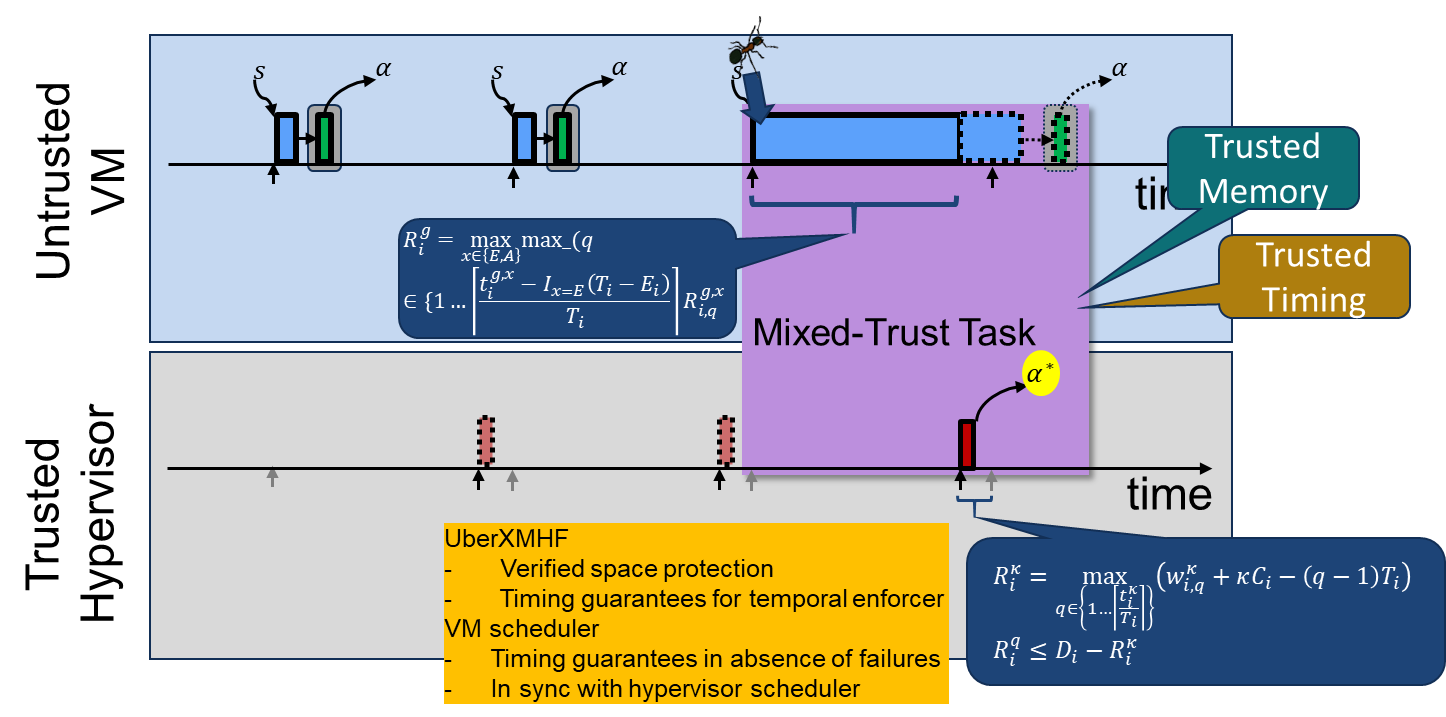
The mixed-trust task scheduling requires two schedulers: one running in the VM that schedules the GT preventing interference between GTs with budget enforcement. However, since the whole VM can be compromised the scheduler in th HV schedulers the HT protecting both its memory integrity and timing. The scheduler in the HV is implemented as a non-preemptive scheduler in order to simplify the logical verification of the HT given the lack of mature tools to verify interleaving functions. However, in the VM a preemptive scheduler is used. To guarantee deadlines for the whole mixed-trust tasks new schedulabiltiy equations for the mixed-preemption scheme and coordination where developed. In this combined scheduling scheme an enforcement timer E for each mixed-trust task is calculated as the last time when the HT can wait before it needs to execute to complete by the deadline. The following figure depicts an intuition of this scheme.
Our implementation was tested for temporal GT timing failure (failed to finish). The following figure presents a timeline of two mixed-trust tasks whose failures cause the execution of their respective HT (in gray patterns).

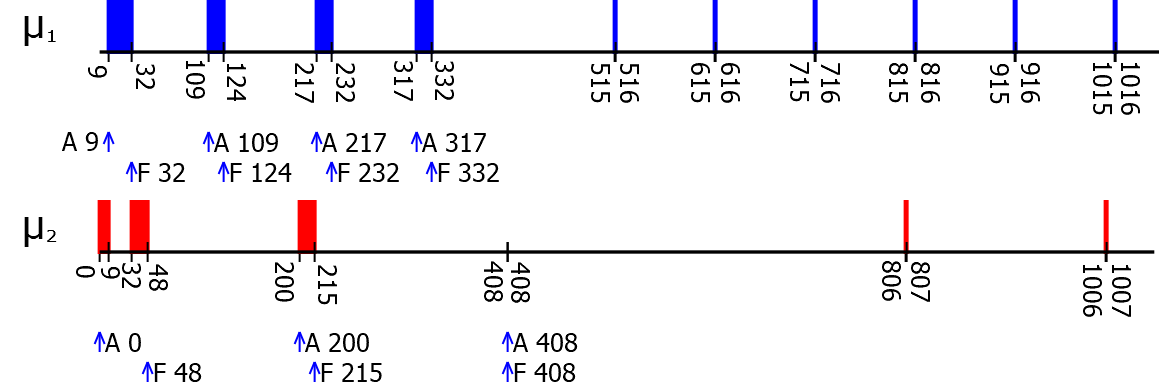
Similarly, we run experiments where the VM was killed completely with a call to panic from a kernel module and verified that the HTs were still running. The following figure shows a plot of such an experiment. All executions after 408 are HTs.
This video shows how a trusted component is used to make sure misbehaviors of the untrsuted components (or even attacks) do not crash the drone. You can see a drop of the drone that is "catched" by the trusted component (enforcer) ensuring that it does not crash. This particular video shows the enforcement behavior verified from the control-theoretic point of view relying on Lyapunov functions.
This video shows that even when the kernel crashes the drone can still keep hovering that is the behavior enforced by the trusted component
Copyright © 2011 Dionisio de Niz · Template design by Andreas Viklu