The objective of this laboratory is for you to analyze the frequency response of a first-order dynamic system, in this case, a filter circuit. You will learn how to measure the amplitude and phase of a frequency response function (FRF), also known as a transfer function, and to develop a physical feel for what FRF's mean.

Frequency Response Functions (FRF) have the interpretation of being the response amplitude as a function of driving frequency.

The simple circuit you will be analyzing is shown below. Its behavior is defined by the time constant t = RC:

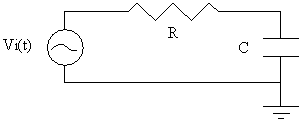
From the standpoint of frequency response, we are interested in the steady state behavior when the input is sinusoidal

The amplitude and phase of the Frequency Response Function (FRF) when it is measured across the capacitor,

f = - ArcTan (wRC)

Assignment:

1. Prepare the Amplitude (V_out/V_in) versus frequency (f) and Phase (f) versus frequency (f) plots. These are called Bode Plots. You will compare these plots to the experimentally obtained Bode plots, for this reason please pay attention to the following points;

• In above equations, in place of w substitute 2pf before plotting. w is in radians/sec and f is in Hz or 1/sec.
• Frequency span should be from 10Hz to 10000Hz.
• Frequency axis (x-axis) should be in logarithmic scale.
• f  is in radians, convert it to degrees by multiplying 180/p.

2. Derive expressions for the amplitude and phase of the Frequency Response Function (FRF) when output voltage, V_out is measured across the resistor, instead of the capacitor as above. Hand in your solution with the lab report, and include it as part of the analysis section.

3. Plot the amplitude and phase expressions obtained in Question#2 by following the same instructions given in Question#1.

Submit your answers to these questions with the lab repost, as a part of Analysis section

1. You will need the following equipments: oscilloscope, spectrum analyzer, function generator, multimeter, printer, BNC cable, T-connector, BNC-clip cables, protoboard, a resistor, and a capacitor.

2. Using the multimeter, measure and record the resistor's value.

3. Build the simple circuit on the prototyping board, using the resistor, capacitor. Refer to the white board in the lab to see how to make common connections on the protoboard. After building the circuit make the following connections;

• Attach a T-connector to output of function generator.
• Connect one side of the T-connector to Channel 1 of oscilloscope using a BNC cable.
• Connect a BNC-clip cable to the other side of the T-connector. Attach the red clip of this BNC-clip cable to resistor's free leg and attach the black (ground) clip to the capacitor's free leg.
• Connect another BNC-clip cable to Channel 2 of oscilloscope. Attach the red clip to capacitor's hot leg and black clip to grounded leg to measure the output across the capacitor.

4. Although you can estimate the time constant from the values of R and C, we don't know C precisely. Further, there are additional sources of resistance in the probes and circuit connections. Hence, you will directly measure the circuit's time constant. Drive the circuit with a square wave input, with the square wave having a frequency of 50Hz and peak to peak amplitude of 2V. (Note: to set 2Vpp, you need to enter 1Vpp on function generator. The input to the circuit is on Channel 1 and output voltage across the capacitor is on Channel 2.

• Display Channel 1 on upper half and Channel 2 on lower half of the screen.
• Set oscilloscope voltage scale for both Channel 1 and Channel 2 to 1V.
• Set time scale to 2 ms.
• Using the cursors, pick-off 4 data points from Channel 2 display to determine the time constant of the circuit. Collect all the data on either exponential-fall or exponential-rise part of the response. Record both time and voltage values of each points. Make sure that measurement cursor source is set to channel 2. For now, do not make any calculations, just collect data points, the detailed information how to calculate time constant using these data points is supplied in Question 1 of Lab Report part.
• Print this screen and include in your report.

   

5. Switch the input to a sine wave, do not change the input amplitude. You will drive the circuit at three different frequencies: one well-below the cut-off frequency (20Hz), one near the cut-off frequency (200Hz), and one well-above the cut-off frequency (2000Hz). The objective here is to see, in the time domain on the scope, the amplitude and phase shifts that occur in the circuit's response at each of these frequencies. Start with 20Hz frequency Sine wave, display the input and output signals on the scope, measure the output amplitude and phase shift. In measuring phase shift, make sure that you set 360 degrees correctly, repeat this setting for each frequency. Make a hardcopy plot of this screen to be included in your report. Then repeat the measurements for 200Hz and 2000Hz, and print these screens too.

6. Now, you will generate Bode plot using the spectrum analyzer.

• While leaving everything connected, move the T connector from the function generator output to the signal analyzer Source.
• Move the cables from channels 1 and 2 on the oscilloscope to input channels 1 and 2 on the spectrum analyzer.
• Turn off the oscilloscope and function generator, and turn on the spectrum analyzer.
• Press INST MODE button on MEASUREMENT menu.
• Select SWEPT SINE by pressing F4.
• Press FREQ button on MEASUREMENT menu.
• Press F3 to select START frequency and set it to 10Hz.
• Press F4 to select STOP frequency and set it to 10000Hz.
• Select RESOLUTION SETUP by pressing F10.
• Set AUTO RESOLUTION to ON by pressing F4.
• Select MINIMUM RESOLUTION by pressing F6, then set it to 401 pts/sweep (F1).
• Press SOURCE button on MEASUREMENT menu.
• Press F2 to set LEVEL, then enter 2 Vpk (F6).
• Press yellow START button on MEASUREMENT menu.
• When the experiment completed, press DISP FORMAT button on DISPLAY menu and select BODE DIAGRAM by pressing F9.
• On DISPLAY menu, select TRACE COORDINATE button and press F1 to select LINEAR MAGNITUDE.
• Press SCALE button on DISPLAY menu and set AUTOSCALE to ON by pressing F1.
• This is the frequency response when the output voltage is measured across the capacitor. Print this screen; press PLOT/PRINT button on SYSTEM menu, then press F10 for MORE SETUP and F2 to select DEVICE IS PRNT, then F10 for RETURN. Finally press F1 to START PLOT/PRNT.

• Detach the measurement clips from capacitor's legs and attach them to the resistor's legs. Make sure that red clip attached hot side and black clip is attached ground side.
• Press yellow START button on MEASUREMENT menu.
• When the experiment completed, press DISP FORMAT button on DISPLAY menu and Select BODE DIAGRAM by pressing F9.
• On DISPLAY menu, select TRACE COORDINATE button and press F1 to select LINEAR MAGNITUDE.
• This is the frequency response when the output voltage is measured across the resistor. Print this screen too, to print press PLOT/PRINT button on SYSTEM menu, then press F1 to START PLOT/PRNT.

1. Determine the time constant of the circuit in following ways;

• Calculate the time constant directly multiplying R and C.
• In step 4, the transient response of the RC circuit will behave as follows:

  

  Plot the logarithm of the measured voltage values versus time. From a linear fit to the data, determine the time constant.

• Using the plot obtained in step 4, determine time constant using initial slope method.
• Compare theses values and which one do you think more accurate, and why?

2. Prepare a table to compare amplitude and phase values for the three frequencies (20Hz, 200Hz, 2000Hz). In this table, list the results obtained in step 5, step 6 and predicted (numerically calculated) values. Keep in mind that amplitudes in Bode plot are in terms of Vout/Vin. Hence, the results of Step 5 (Vout measurement) should be divided to Vin to be able to compare them on the same ground. Also, are all the results same, answer both qualitatively and quantitatively, is there any difference, if so what is it and why?

3. Discuss the differences between the transfer functions in part 6 and 7, and compare them with those predicted theoretically. Basically discuss the manner in which these two filters (output across the capacitor, or across the resistor) alter an input signal with a range of frequencies.