TIRM is a technique for monitoring the instantaneous separation distance h between a microscopic sphere and a flat plate (often a glass microscope slide). This page describes how we obtain the potential energy (PE) profile f(h) of interactions between the sphere and the plate.
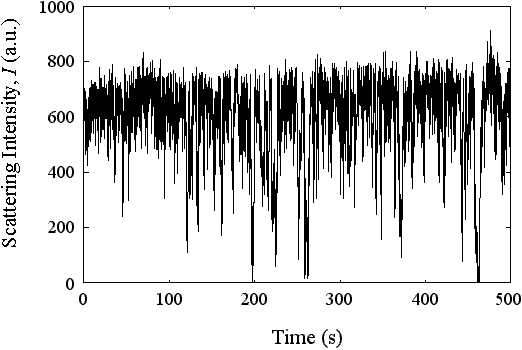
After taking one measurement, we wait for the distance to change by Brownian motion before taking a second measurement. We then repeat this process a statistically large number of times: typically we take at least 50,000 measurements of the separation at 10 ms intervals. The figure below shows some typical raw data observed with a 10 mm PS latex sphere undergoing Brownian motion in 0.5 mM NaCl solution.

We then form a histogram of these 50,000 measurements.
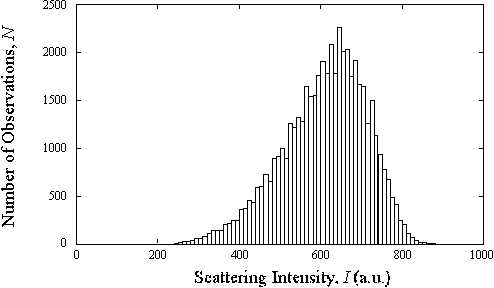
If the particle has had time to sample all elevations a statistically large number of times, the shape of this histogram converges to the shape of the probability density function p(h) appearing in Boltzmannís equation:
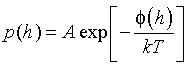
where p(h)dh is the probability of finding the sphere between h and h+dh, f(h) is the PE of the sphere at elevation h, kT is the thermal energy and A is a normalization constant whose value is chosen such that ![]() = 1.
= 1.
In essence, TIRM is then capable of directly measuring this probability density function. Knowing p(h), we can turn Boltzmannís equation "inside-out" to deduce the PE profile f(h): to eliminate A, we divide this equation by itself evaluated at some reference position denoted hm before solving for the PE. This leaves
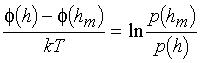
Usually hm is chosen as the elevation corresponding to the minimum in f(h). Since Boltzmannís equation defines the mean potential in statistical mechanics, we claim that TIRM directly measures the PE profile.