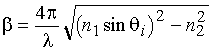

TIRM is a optical technique for monitoring the instantaneous separation distance between a microscopic sphere and a flat plate. Changes in distance as small as 1 nm can be detected. To determine the instantaneous separation distance, we measure the intensity of light scattered by the sphere when it’s illuminated by an evanescent wave. The image at right is a 6 mm polystyrene bead in water viewed from above through a microscope. In this view (which has been cropped), the bead is illuminated both by a evanescent wave (red) and the lamp from the microscope (white). The set of large white concentric rings is the outline of the bead as seen through a normal microscope, whereas the set of smaller red rings is the light scattered from the evanescent wave. During an experiment, the microscope's lamp is turned off and the sphere appears as a bright red spot on a dark background. The intensity of the spot flickers with time as the distance between the bead and the plate changes due to Brownian motion.

When a sphere with a refractive index different from that of the water settles near an interface at which total internal reflection occurs, some of the evanescent wave is scattered as shown in the figure at right; this situation is called "frustrated" total internal reflection. Because of the nonuniform illumination of the water by the evanescent wave, the amount of light scattered by the sphere is exquisitely sensitive to its proximity to the interface.
Prieve & Walz devised a method for placing the sphere a known and adjustable distance from the wall, and measuring the scattering intensity as a function of distance. A MgF2 film was sputtered onto a glass slide which serves as a spacer to separate the PS sphere from the glass plate by a distance equal to the known film thickness. The fluid (a mixture of propanol and ethanol) was chosen to have the same refractive index as the film; then the interface between the outer film and the fluid disappears, leaving the same scattering geometry as in our usual TIRM experiments.
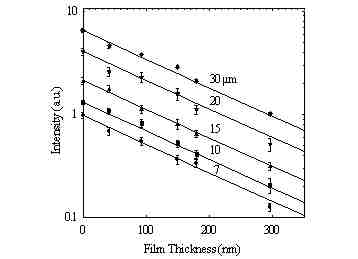
The graph at right summarizes the measured scattering intensity as a function of film thickness for spheres of different diameter. The results for different size spheres have been offset for ease of viewing. Each point is the average of about 20 measurements for different spheres of the same diameter, which scatter quite differently (possibly due to different density inhomogeneities within each particle). The lines all have a slope b calculated from
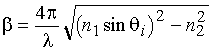
where b-1 is the penetration depth of the evanescent wave intensity, l is the wavelength of the incident light, n1 and n2 are the refractive indexes of the plate and the fluid containing the particle, and qi is the angle of incidence in the plate. The points representing average scattering intensities virtually all fall within experimental uncertainty of these lines. This confirms the ray-optics predictions that the scattering intensity I decays with the same dependence on distance from the wall as the intensity of the evanescent wave itself:
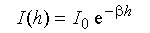
Typically b-1 is about 100 nm in our experiments with glass microscope slides in aqueous solutions. Because of this exponential sensitivity, a very small change in h produces a measurable change in intensity. For example, we estimate that the photomultiplier tube we use to quantify the light intensity can realistically detect a 1% change in intensity. According to with b-1 = 100 nm, a 1% change in I corresponds to a 1 nm change in h. Thus we can detect changes in h of the order of 1 nm, which represents the current spatial resolution of the technique.
To obtain absolute separation distance, we need a value for I0 in the equation for I(h) above. The data in the graph above show that the equation for I(h) holds for all separations including contact (h = 0) despite the possibility of multiple reflections between the sphere and the plate (provided the sphere is not too large). Thus I0 can be directly measured by forcing the sphere into intimate contact with the wall. For spheres levitated by double-layer repulsion, this can be accomplished by increasing the ionic strength of the solution to about 10 mM. Then double-layer repulsion is sufficiently weakened that van der Waals attraction causes the sphere to jump into intimate contact, allowing I0 to be measured.
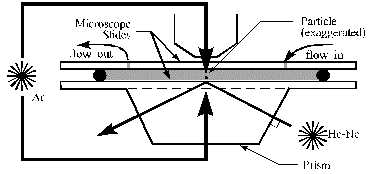
The sketch at right shows a schematic of the current TIRM flowcell. A syringe is used to inject salt solution containing latex particles (typically 3 to 30 mm in diameter) between two microscope slides optically coupled to a dove-tail prism. The two slides are held about 1 mm apart using an o-ring as a spacer. After 10-20 minutes, the particles have settled near the lower slide. The flowcell is mounted on a specially designed micrometer stage, which allows 3D motion relative to the objective lens of the microscope. This stage is adjusted until a single levitated particle is in the field of view of the objective lens and the particle appears focussed.
Depending primarily on the pre-treatment of the glass slide, some or all of the particles might stick to the glass. A stuck particle will not move when additional fluid is injected into the flowcell. Sticking is usually the result of insufficient charge at low ionic strengths (in the case of double-layer repulsion; or insufficient adsorbed polymer, in the case of steric repulsion) on the surface of either the sphere or the plate. To increase the negative charge on the glass plate, we soak our slides in a basic solution before rinsing and mounting in the TIRM apparatus. Similarly, dilution of surfactant-stabilized particles might cause desorption of the ionic surfactant, loss of charge, and sticking of the particles. This can be avoided by using sulfonated or carboxylated latexes having covalently attached charges; or the particles might be dispersed in a solution of anionic surfactant like SDS. Of course, the total ionic strength must also be kept below about 5 mM to keep most of the particles levitated.
A 30 mW helium-neon laser beam is made incident to the water-glass interface at an angle greater than the critical angle so that total internal reflection results. A reproducible angle of incidence is accurately set by adjusting a mirror mounted on a rotating micrometer stage until the beam reflected off the incident face of the prism practically coincides with the incident beam; this gives normal incidence for the external reflection at the air-glass interface and an angle of incidence for the internal reflection at the glass-water interface equal to the angle between the two faces of the prism (68°). The rotating stage containing the mirror is in turn mounted on a 2D translation stage which is now adjusted until the light scattered from the particle is maximized; this corresponds to centering the internal reflection under the particle.