| home |
| apparatus |
| procedure |
| data |
| bibliography |
| contact |
Any solid in contact with a liquid acquires some immobilized charge on its surface by dissociation, complexation, or adsorption. The immobile charge on the surface attracts an exact number of excess ions from the liquid to shield the surface charge in order to make the interface neutral. This is the basic mechanism of formation of the so-called electrical double layer. One layer is the plane of charge and the other is a space charge distribution held near the solid by a balance between electrostatics and diffusion. One consequence of this space charge distribution is that a position-dependent electrical potential within it varies from zero far from the surface and reaches a maximum in magnitude very near the surface.
The zeta potential of a surface is the value of this position-dependent electrical potential within the space charge region at the plane of shear, i.e. the location near the surface where the local velocity deviates from zero when there is flow of liquid in the vicinity of the surface. This specification arises from the method by which one commonly deduces the zeta potential of a planar surface. One typically measures a streaming potential near the surface that arises when liquid flows by it, sweeping mobile charge in the diffuse layer along with it. An equation depending on the details of the system then converts the measured streaming potential to zeta potential. Because the streaming potential depends on shearing the fluid adjacent to the surface, and because only charge that is outside the plane of shear contributes to the streaming potential, the zeta potential is naturally associated with the plane of shear.
For a thorough discussion of zeta potential, see [Hunter81].
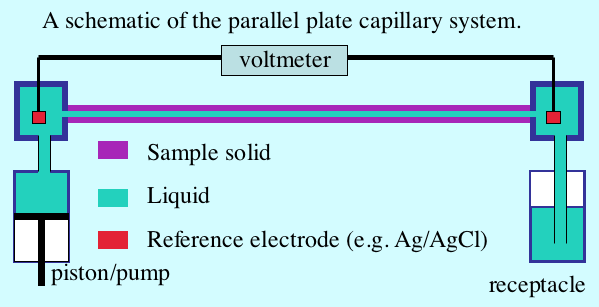
The Classical Measurement System: the parallel plate capillary
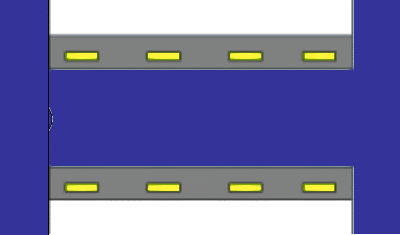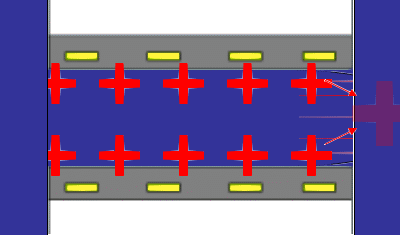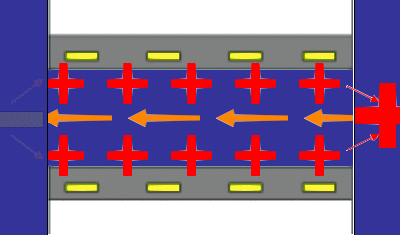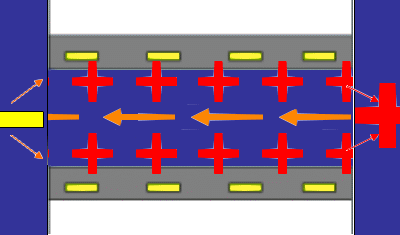
The principles underlying the most common method for measuring a steaming potential appear in the accompanying animation, (not to scale). Two charged planar surfaces are separated by a distance large with respect to the Debye length. In the animation, the solid surfaces are negatively charged. Liquid, driven by a pressure difference from inlet to outlet, flows laminarly with a parabolic profile between the plates. The liquid sweeps along the mobile charge of the diffuse part of the electrical double layer (in this case positive) associated with each surface. The flow of mobile charge is an electric current arising solely from the flow of liquid; we call this a “surface current” having units of A/m. If there is no net flow of charge from the solid surfaces to the solution, a bulk current carried by neutral electrolyte must flow back through the liquid to complete the electrical circuit. The animation represents this bulk current as the orange arrows emanating from a positive pole at the flow outlet. The bulk current flows back to a negative pole at the inlet and completes the electrical circuit. One uses reference electrodes placed at either end of the flow channel to detect the streaming potential. Of course all these phenomena are occurring in parallel in a real system. The animation merely suggests the order of consequence described above.
The classical equation for calculating zeta potential from streaming potential measurements in the parallel plate capillary system is given below. Note that this equation neglects surface conductivity for simplicity of presentation. When making streaming potential measurements on a parallel plate system, correction for surface conductivity might be necessary.

A schematic of apparatus for measuring zeta potential with a parallel plate system appears in the figure below. The flow channel is quite narrow in order to sustain a substantial pressure gradient at a relatively small flow rate. Reference electrodes placed in wells at either end of the capillary detect the streaming potential. When the piston pushes liquid from left to the right the voltmeter registers the streaming potential.
ZetaSpin: a revolution in zeta potential measurement
The ZetaSpin zeta potential measurement is based on the well known hydrodynamics of a rotating disk [vKarman21, Cochran34, Rogers60]. ZetaSpin shares some fundamental features with the classical method of zeta potential measurement but has some notable differences. The common elements are that flow of liquid near a solid surface generates surface current that must return as bulk current through the electrolyte in order to complete the circuit. Rotation of the disk generates a fully three-dimensional axisymmetric flow. The crucial feature for the purpose of zeta potential measurement is the radial flow generated near the disk surface. This flow sweeps positive charge in the diffuse layer outward to the periphery of the disk where it leaves the diffuse layer and flows back though the liquid toward the axis to complete the circuit.
The animation suggests this logical sequence by the motion of positive charge outward along the disk surface and back through the solution. Thus the positive and negative poles at the ends of the parallel plate cell have their equivalents in the rotating disk geometry; they appear at the disk periphery as a ring-shaped source or sink of current and at the center of the disk. The lines appearing in the animation are lines of constant streaming potential (full lines) and lines of current flow (dotted). The animated positive charge follows one line of current.

The equation by which one converts the measured streaming potential to zeta potential is given below. It is assumed that one reference electrode is at least one diameter away from the disk and that the other reference is centered on the axis and located a distance z from the plane of the sample. This equation is accurate to 1% when z is no more than 10% of the disk radius.

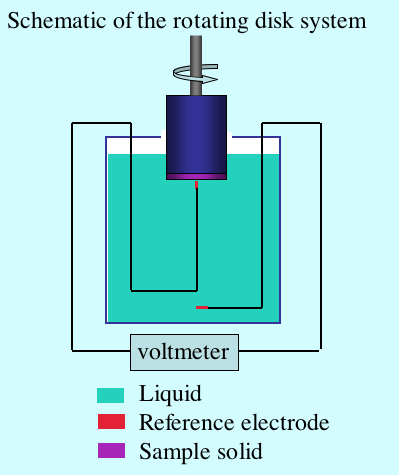
A schematic of the rotating disk system showing the primary components appears in the figure below. A motor rotates a spindle to which a cylindrical sample support is attached. The sample is affixed on the end of the cylinder. One reference electrode is positioned near the sample on the axis of rotation and the other reference electrode is positioned far from the sample. When the sample is rotated, the voltmeter registers the streaming potential.
For more detail about the theory of the rotating disk for measurement of zeta potential, download this document: "Theory of Zeta Potential Measurement" and see the publications of Sides et al. in the Bibliography. Note that there is an error of calculation in [Sides04] and [Hoggard05] that is corrected in subsequent articles [Sides06].
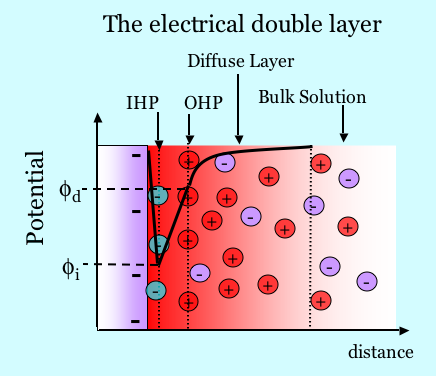
The figure below illustrates schematically the electrical double layer. A plane of charge due to complexation or dissociation exists on a surface. For example, consider in this case that the total charge is negative as shown in the figure below. It may also be the case that ions from solution are specifically absorbed, as shown by the negatively charged green species. Counterions attracted to the surface by electrostatics shield the surface charge. The counterions are not all in the same plane, however, because they are held in a dynamic balance by electrostatic attraction and the tendency to diffuse away. The concentration of ions in the diffuse layer decays with distance from the surface. Thus the surface charge forms one layer and the diffuse shielding charge forms the other layer, hence the term “double layer”. The double layer has a certain structure. The Inner Helmholtz Plane (IHP) is the plane cutting through the center of the adsorbed species. The Outer Helmholtz plane (OHP) is the plane cutting through the positive ions at their position of closest approach. Ions in the diffuse layer are always being exchanged at the surface, but the surface excess of counterions always exactly balances the total charge associated with the solid. The Gouy-Chapman theory describes the physics of the diffuse part of the double layer. One solves Poisson’s equation where the charge density is given by the Boltzmann distribution of charge in the diffuse layer. Many basic texts in physical chemistry and colloid science discuss details of the double layer.
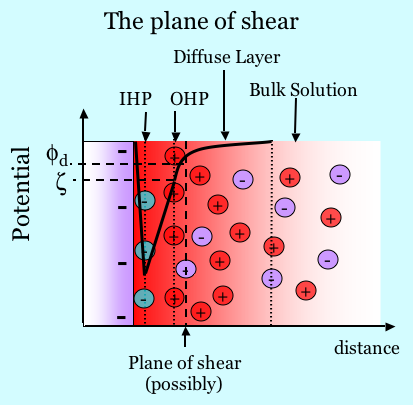
The zeta potential is the electric potential at the plane of shear. Since zeta is typically probed and measured based on its response to motion of a solid relative to a liquid, one must realize that there are cases where the Outer Helmholtz Plane is not co-planar with the plane of shear, as shown in the graphic below. For example, if there is a brushy polymer adsorbed that is itself uncharged, the part of the diffuse layer charge that is inside the brushy layer does not necessarily move when fluid flows near it. Diffuse layer charge that does not move laterally in response to shear does not contribute to the streaming potential and thus does not contribute to zeta. In many if not most circumstances, the zeta potential is essentially equivalent to the potential at the OHP. See [Hunter81] pp 210 - 216 for a discussion.
Surface conductivity
Surface conductivity provides essentially a parallel path for current to flow back through the double layer; its effect typically is to diminish the determined zeta potential. The surface conductivity comprises two effects: (1) There is an effective surface excess of mobile ions in the diffuse part of the double layer. (2) The component of the bulk electric field parallel to the surface in a streaming potential measurement drives motion in the diffuse layer, which appears as an enhancement of conductivity. It has been found that correction for surface conductivity in zeta potential measurements via a streaming potential method is necessary for the case of the parallel plate capillary. A correction for surface conductivity is not necessary for the ZetaSpin measurement because the return path through the electrolyte provides a much lower resistance. See [Newman04] Chapter 9 and particularly the problems at the end of the chapter for a careful discussion.
The Debye Length is a parameter having units of length that characterises the thickness of the diffuse layer. Usually written as the variable l, the Debye length is inversely proportional to the square of the ionic strength. For example, its value is 0.96 nm is a 0.1M solution of a 1:1 salt. Thus its value would be 9.6 nm for a 1 mM solution of the same salt. Standard textbooks of physical chemistry and colloid science discuss this parameter.