

Statistical Physics attempts to explain macroscopic phenomena in terms of underlying microscopic laws. The large-scale behavior of systems, which we characterize by means of a small number of variables, emerges after eliminating the many microscopic degrees of freedom of their fundamental constituents. These generally unobservable degrees of freedom are far too numerous to follow, but precisely for this reason they can be treated statistically, making use of the law of large numbers and the central limit theorem: averages of a large number of random variables tend to converge to well defined distribution functions, and their relative fluctuations become smaller than other experimental errors. For instance, the pressure of a gas, the electric conductivity of a wire, or the Young modulus of rubber result from a proper statistical treatment of gas molecules, electrons in a solid, and entangled polymer chains, respectively. For this reason, Statistical Physics is the microscopic foundation of Thermodynamics.
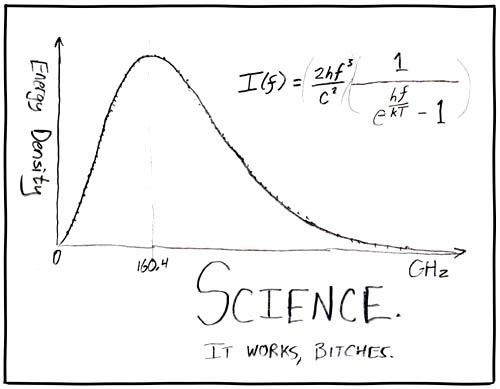
The key topics to be covered in every "Introduction to Statistical Physics" course only vary in small degrees. Central to all discussions is an understanding of some essential probability theory, statistical ensembles, the connection to thermodynamics, various illuminating model systems (such as the ideal gas or the harmonic crystal), and some good approximation schemes to deal with all those problems that can’t be solved exactly. In this course, we will begin with the (classical) ideal gas, introduce the notion of entropy, then move on to an overview of thermodynamics, and return to visit statistical mechanical ensembles (microcanonical, canonical, grand canonical). The necessary probability theory will be filled in as we go. We then extend the treatment to quantum statistical physics, visiting some of the famous example problems like black body radiation and Bose-Einstein condensation.
Exams
There will be one midterm and one final exam, the dates of which will be announced soon.
| Midterm | Wednesday, March 18; during regular class time; closed book, no notes. |
| Final Exam | Date and time to be determined by the registrar.. No notes, closed book. |
Dept of Physics | 5000 Forbes Avenue, Pittsburgh, PA 15213 | (412) 268-2740
|
|
|
 |
|
Units: 12 Prerequisites: none*
Lecture: MWF 9:30-10:20, DH A301D
Recitation: M 1:30-2:20, DH A200
Course limit: n/a
* It seems I should qualify "none" a bit. This is an introductory course, and as such I assume little to no previous exposure to the topic. But since this is also a graduate course, I expect that you are reasonably comfortable with what is usually perceived as the standard undergraduate physics and mathematics curriculum, such as calculus and algebra, as well as the basics of quantum mechanics. So "none" should be read as "none at the graduate level".