| Lecture
#17 |
Chapter 14 starting
with Section 2
(We'll return to Section 1 later)
|
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
| Lecture Outline (some material shown is
look-and-listen only) |
Quantum Theory of the Chemical Bond
Molecular orbitals (in "homonuclear diatomic
molecules"
Approximated by combinations of atomic
orbitals
Constructive and
destructive interference effects
Combining 1s atomic
orbitals to get molecular orbitals
"Sigma" bonding molecular
orbital
"Sigma" antibonding molecular
orbital
Combining 2p atomic orbitals
"Sigma" bonding molecular
orbital
"Sigma" antibonding molecular
orbital
"Pi" bonding molecular orbitals
"Pi" antibonding molecular
orbitals
|
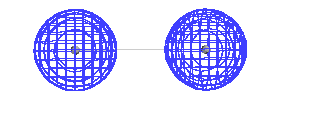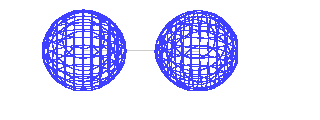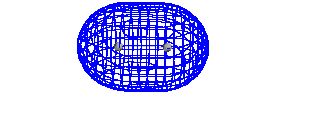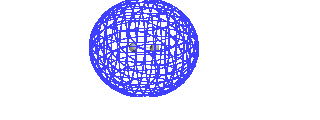
| This is a calculated solution for the constructive
interference result. |
 |
| If destructive interference represents the orbital in
which the electron happens to be found, the linear
combination results in a depeletion of electron density
between the positively charged protons. They repel each
other under these circumstances. |
 |
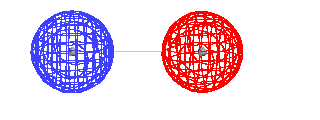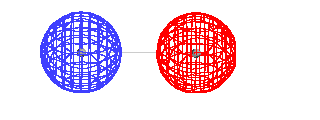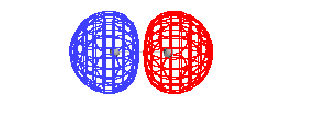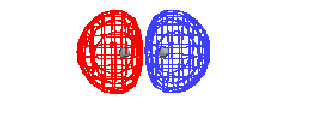
| This is the destructive interference combination of
1s atomic orbitals |
 |
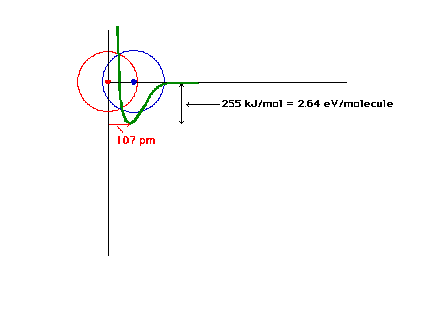
| The total energy of the ground state of H2+
as a function of the distance between the protons. |
 |
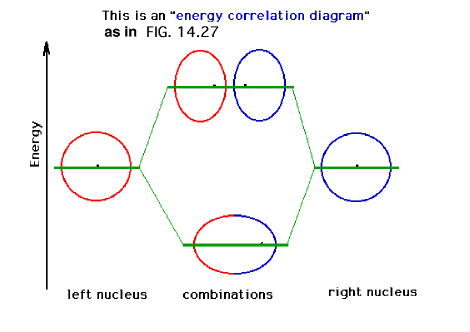
| A schematic of the orbitals on separated protons
relative to "close" protons. The constructive
combination of atomic orbitals gives rise to a system
lower in energy than the isolated system and is a bonding
molecular orbital. |
 |
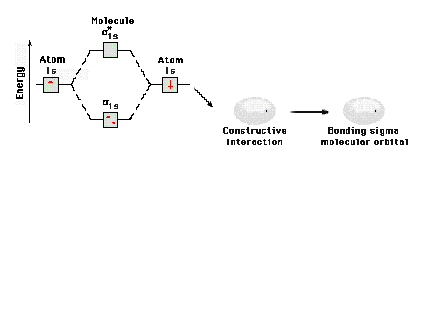
| Energy diagram and geometry for the sigma-1s
(bonding) orbital construction. 
|
 |
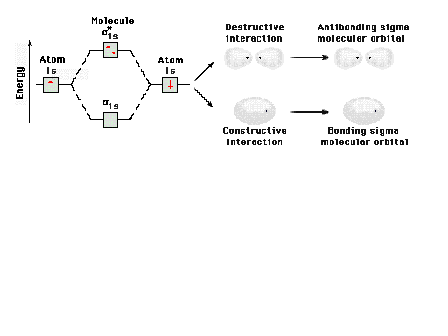
| Energy diagram and geometry for the sigma*-1s
(antibonding) orbital construction 
|
 |
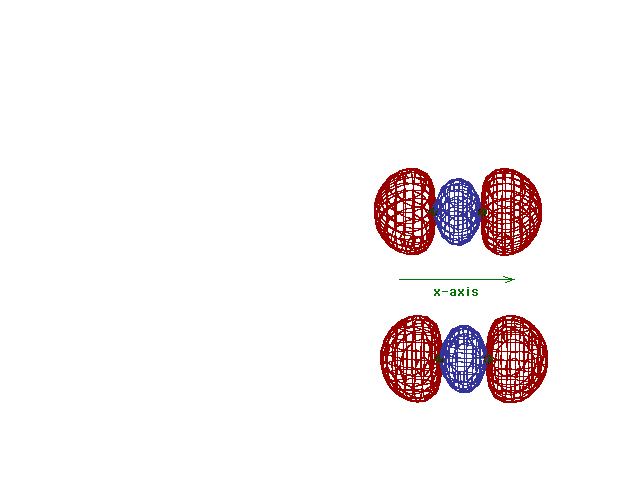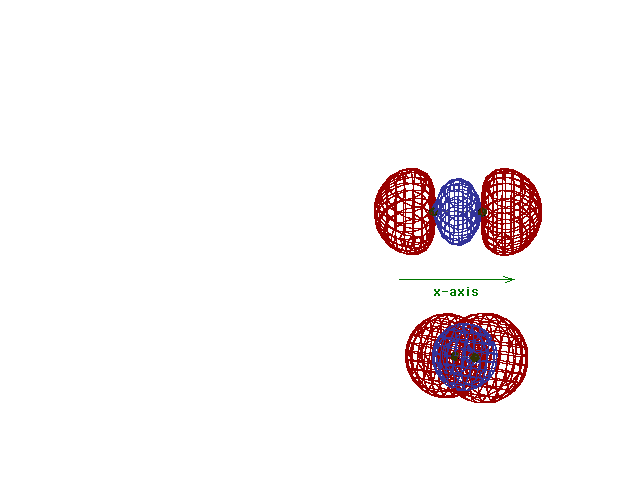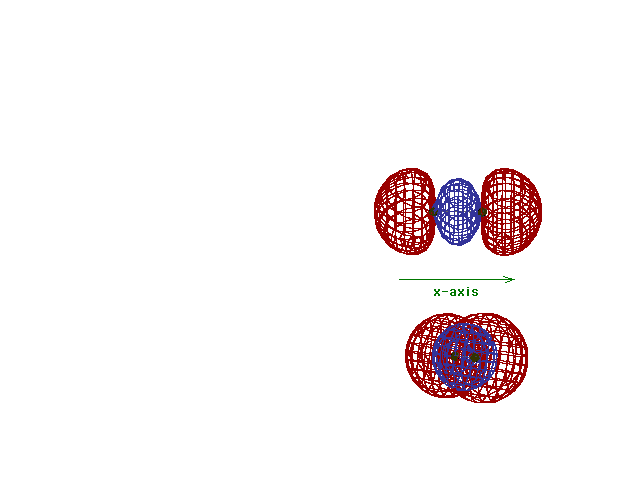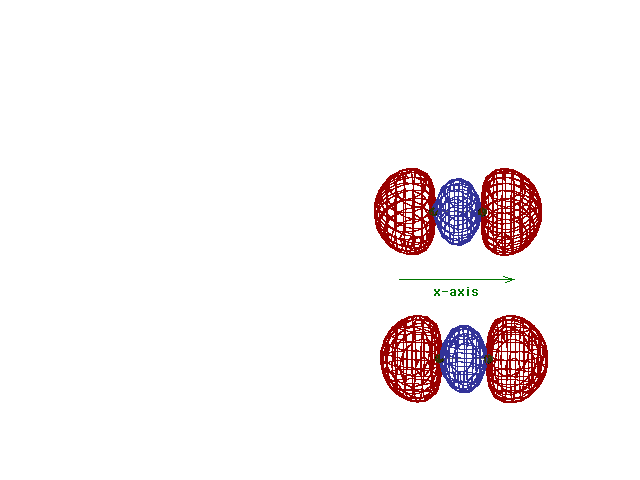
| Energy diagram and geometry for the sigma-2px
(bonding) orbital construction from the 2p atomic
orbitals originally directed along the bonding (x) axis. |
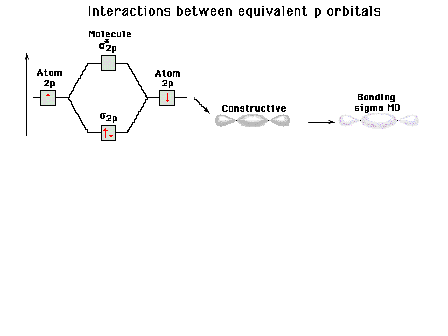 |
This (with luck) is an animation of the
computer-generated  2p
(or 2p
(or  p) bonding
molecular orbital showing how the symmetry about the bond
axis resembles that for the s-atomic orbital's symmetry
about the nucleus. Hence the p) bonding
molecular orbital showing how the symmetry about the bond
axis resembles that for the s-atomic orbital's symmetry
about the nucleus. Hence the  label. label. |
 |
| Energy diagram and geometry for the sigma*-2p
(antibonding) molecular orbital construction |
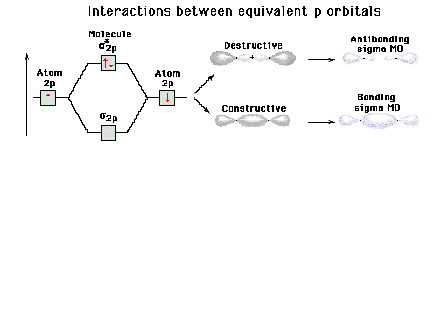 |
| A reminder that, perpendicular to the bond axis in
the x-direction, there are 2p atomic orbitals in the
z-direction and in the y-direction. Just the 2py
orbitals on each atom are shown here. |
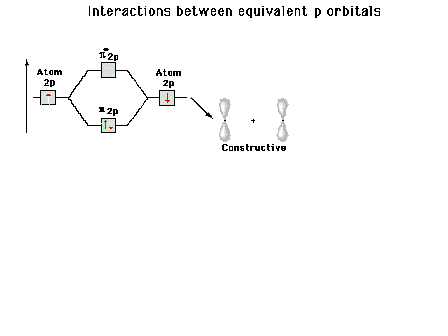 |
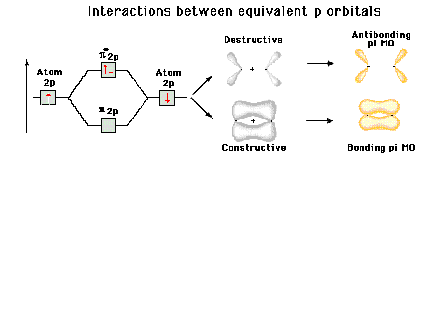
| Energy diagram and geometry for the pi-2py
(bonding) molecular orbital construction from the 2p
atomic orbitals originally pointing in the y-direction,
perpendicular to the bond axis and in the plane of the
illustration. Constructive interference occurs in the
region of overlap. (Recognize that there is an identical
pi bonding level, same energy, constructed in the
x-direction from the 2pz atomic orbitals.) |
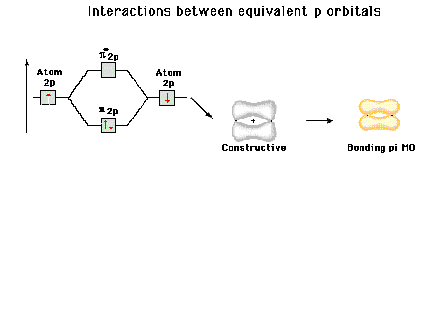 |
This is an animation of the computer-generated  2p
bonding molecular orbital showing how the symmetry about
the bond axis resembles that for the p-atomic orbital's
symmetry about the nucleus. Hence the 2p
bonding molecular orbital showing how the symmetry about
the bond axis resembles that for the p-atomic orbital's
symmetry about the nucleus. Hence the 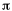 label. label. |
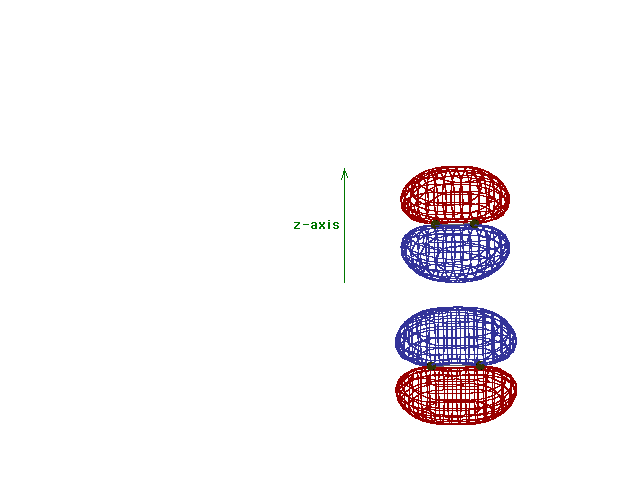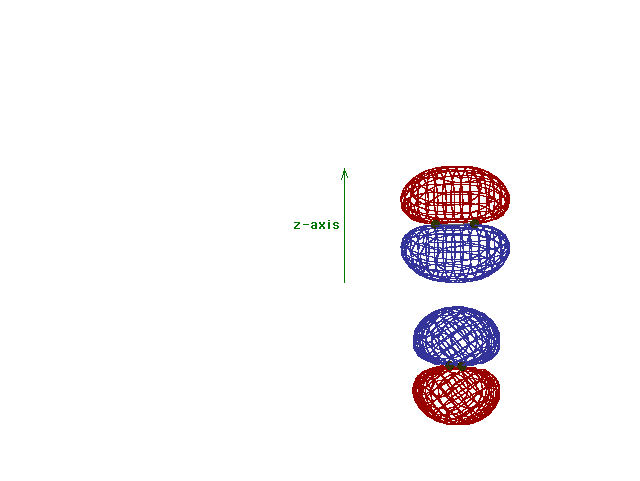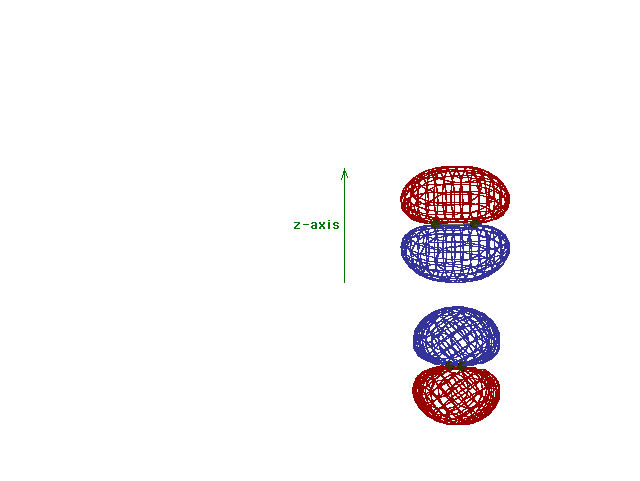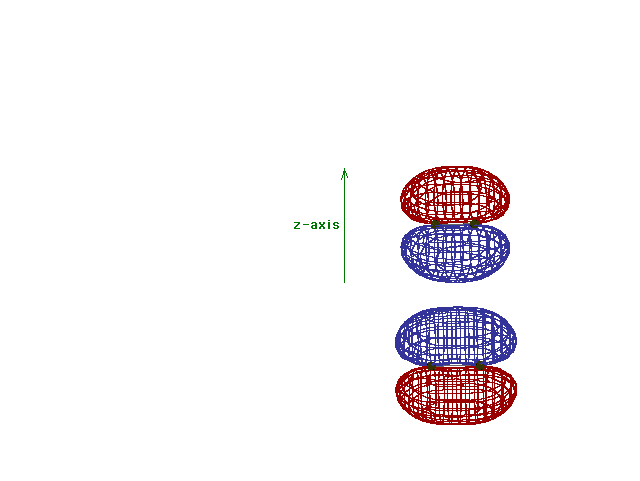 |
| Energy diagram and geometry for the pi*-2py
(antibonding) molecular orbital construction from the 2p
atomic orbitals originally pointing in the y-direction,
perpendicular to the bond axis and in the plane of the
illustration. Destructive interference occurs here, in
contrast to what occurs for the bonding molecular
orbital. (Recognize that there is an identical pi*
antibonding level, same energy, constructed in the
z-direction from the 2pz atomic orbitals.) |
 |
| Re-defining how one calculates bond order within the
context of molecular orbital theory. |
 |
The molecular orbital energy diagram for H2-
and other isoelectronic species, all having bond order =
0.5. The electron configuration would be written as 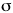 1s2 1s2 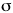 *1s2 *1s2 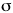 2s2 2s2
or, as in the current text, simply 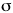 s2 s2
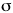 *s2 *s2
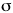 s2. s2. |
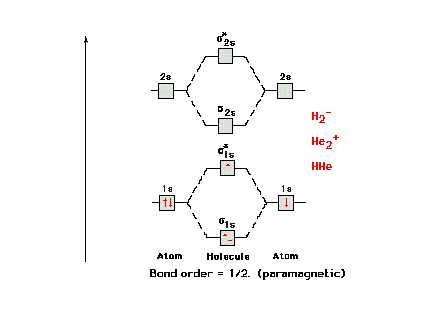 |
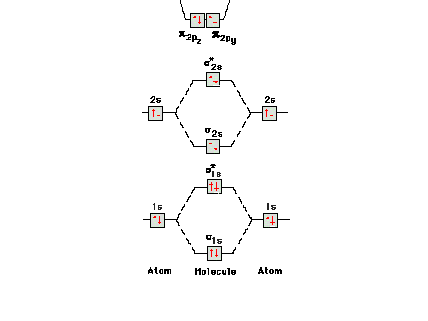
| Molecular orbital energy diagrams for 1, 2, 3, and 4
electrons systems. The correspondence between bond order
and bondlength and between bond order and bond energy is
shown for each molecular species. |
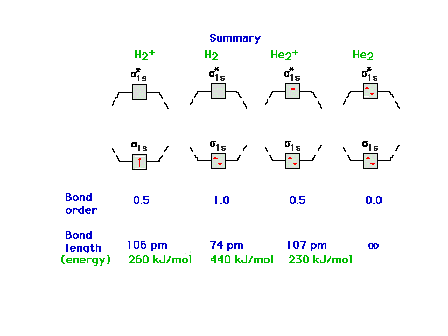 |
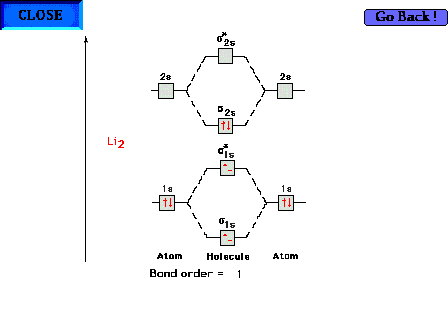
The molecular orbital energy diagram for Li2
containing all six electrons. Since antibonding electrons
negate the effect of bonding electrons, the pair of 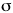 * electrons cancels out the bonding
characteristics of the pair of * electrons cancels out the bonding
characteristics of the pair of  electrons
and both pairs revert to the inner core 1s2
configurations that we expect from simpler
considerations. The electron configuration could thus be
written as [He][He] electrons
and both pairs revert to the inner core 1s2
configurations that we expect from simpler
considerations. The electron configuration could thus be
written as [He][He]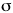 2s2. 2s2. |
 |
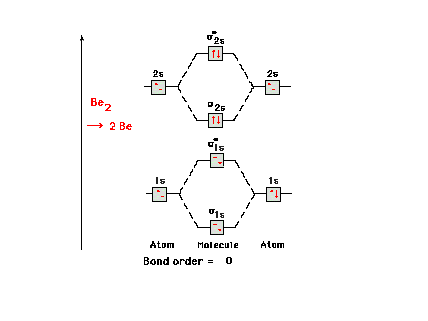
| The molecular orbital energy diagram for Be2.
Since the number of antibonding electrons is equal to the
number of bonding electrons, there is no net bonding in
this molecule and it simply breaks back up into two Be
atoms. |
 |
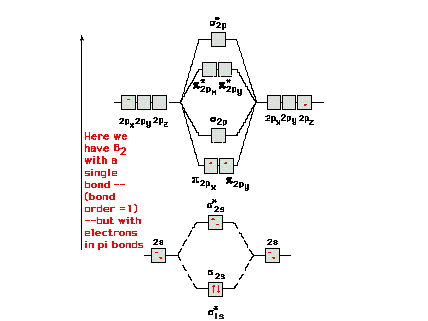
For "diboron", B2 we get a
somewhat surprising result out of the molecular orbital
energy diagram and the ensuing electron configuration.
The ninth and tenth electrons go into the lowest energy
available orbitals. These are the 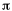 orbitals.
There are two of equal energy and Hund's rule forces us
to put one electron in each and with parallel spins. Thus
we have bond order = 1, a single bond, but it is not a
sigma bond. In fact, there is one electron in one
pi-orbital and another electron in a second pi-orbital
comprising this single bond. orbitals.
There are two of equal energy and Hund's rule forces us
to put one electron in each and with parallel spins. Thus
we have bond order = 1, a single bond, but it is not a
sigma bond. In fact, there is one electron in one
pi-orbital and another electron in a second pi-orbital
comprising this single bond. |
 |
| Molecular orbital energy diagram for the lower states
in molecular nitrogen, N2. The lowest two
molecular orbitals return to 1s, inner core electrons on
each nitrogen atom. The next two pairs, with no net
bonding effect, become lone pairs that can be pictured as
being in 2s valence orbitals on each nitrogen. |
 |
| The valence molecular orbitals in nitrogen that give
rise to the triple bond, bond order = 3. |
 |

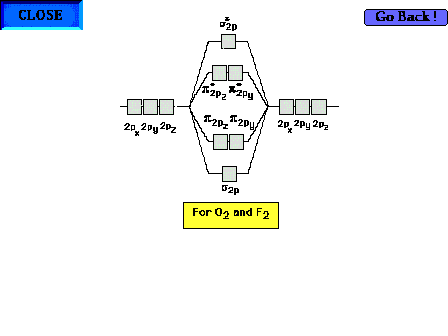
Click the Detour sign to see an optional explanation
(several slides) of why the  / / sequence changes when O2
and F2 are reached. Note, you do not
need to remember this reversal of sequence. For your
convenience in 09-105, you can ignore it even if it seems
to apply. sequence changes when O2
and F2 are reached. Note, you do not
need to remember this reversal of sequence. For your
convenience in 09-105, you can ignore it even if it seems
to apply. |
 |
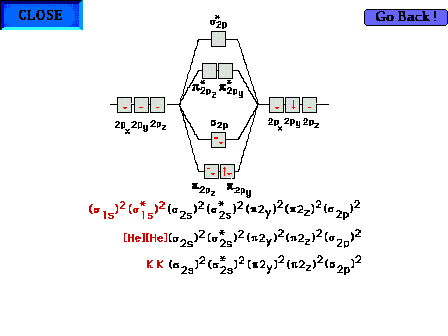
The electron configuration for all 14 electrons in N2.
Three variations are shown on how to represent the inner
core, 1s2 electrons on each nitrogen atom.
Sometimes the two pi molecular orbitals are respresented
with a single  4 symbol. 4 symbol. |
 |
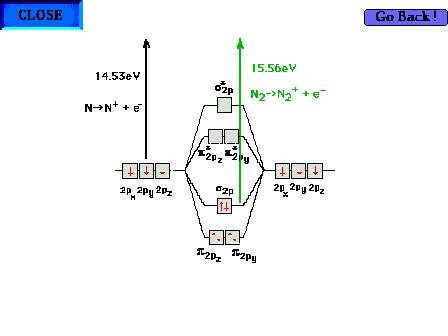
| Comparison of ionization energies for atomic N and
molecular N2 to illustrate that the bonding
molecular orbital in the latter is more stable than the
atomic orbital from which it "originates". That
is, combining two N atoms leads to a more stable, bound
nitrogen molecule, releasing energy. |
 |
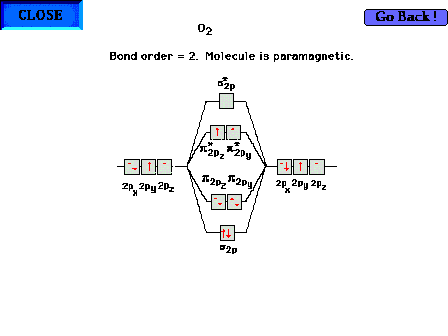
The highest occupied molecular orbitals in molecular
oxygen. The bond order is 2, but is composed of a sigma
bond and one net electron in each of the two 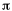 orbitals.
The molecule is paramagnetic due to the two parallel
electron spins. orbitals.
The molecule is paramagnetic due to the two parallel
electron spins. |
 |
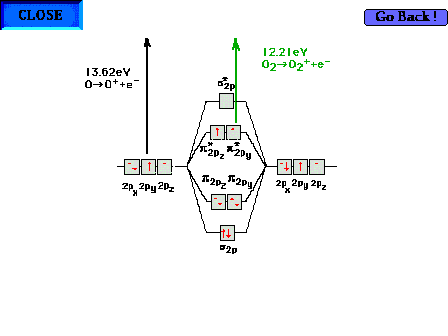
| Comparison of ionization energies for atomic O and
molecular O2 to illustrate that the
antibonding molecular orbital in the latter is less
stable than the atomic orbital from which it
"originates". That is, electrons in the
antibonding orbitals "want" to release energy
by returning to atomic orbitals. |
 |





