1. Homework

Here is a proof of Lemma 1, which I asked you to prove for homework.

Claim: For any whole number p, if p² is even, then p is even.

Proof:

1) Assume that p2 is even.

2) Assume, for reductio, that p is odd.

3) Then there is some whole number r s.t. p = 2r + 1.

4) Thus, p² = (2r + 1)²

5) p² = 4r² + 4r + 1

6) p² = 2(2r² +2r) + 1

7) (2r² + 2r) is a whole number, so there is a whole number q such that p² = 2q + 1, thus p² is odd, contrary to the assumption in step 1. Q.E.D.

2. The Structure of Mathematical Theories: Axioms, Definitions, and Theorems

Mathematical reasoning involves more than just deduction. Mathematical theories are systematized by axioms and definitions in a way exemplified by Euclid in his famous compilation of geometric knowledge in the Elements. Euclid's model of a how to structure a mathematical theory still dominates today. Euclid divided his theory into four parts, each of which he gave explicitly:

- Definitions

- Common Notions (Logic)

- Postulates (Axioms)

- Theorems

The Definitions are supposed to clarify the concepts used in terms of primitives that are completely clear and familiar. We will discuss definitions in more detail later. The Common Notions are to provide rules of logic, that is, rules for making inferences which preserve truth. The Postulates, or Axioms, are the substance of the theory. They provide the sum total of all that one need assume in order to derive the rest of the theory, which is separated into Theorems.

Thus the Axioms are the substantive foundation for the theory. If you believe in the Axioms, and the theorems follow deductively from these Axioms, then you must also believe the theorems. So instead of making us look at hundreds of pages of claims, propositions, etc., we need only look at the Axioms and the proofs. Once the proofs are verified as proofs, we can ask ourselves if the Axioms are worthy of belief.

Axioms

Axioms are the substantive foundation of a mathematical theory. If you believe in the axioms, and the theorems truly follow deductively from these axioms, then you must also believe the Theorems. So in some sense the axioms exhaust the content of the theory. Euclids theory of geometry had 5 short axioms, and from these axioms hundreds of pages of theorems follow. The mathematical theory of probabililty can be reduced to three simple axioms, yet thousands of pages of theorems follow from them. Instead of making us look at hundreds of pages of claims, propositions, etc., we need only look at the Axioms and the proofs. Once the proofs are verified as proofs, we can ask ourselves if the Axioms are worthy of belief.

Imagine two scenarios. In the first, someone hands you 2,000 pages of geometry and says they have found the correct theory of space. They ask you to examine their theory. Do you believe all of its claims? In the second scenario, someone hands you 1 page of axioms in geometry and an accompanying 1,999 volume of theorems. They ask you the same questions, but assure you that the 1,999 pages of theorems follow logically from the 1 page of axioms. In the first scenario your task is almost impossible, but in the second it is relatively easy.

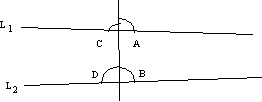
Euclid's geometry was taken to be the paradigm of a good theory. Kant, approximately 2,000 years later, asserted it to be the paradigm case of a synthetic a priori theory, necessary but non-trivial true theory of the way the world is built. Even so, many mathematicians were unhappy with the inelegance of the 5th postulate, the infamous "parallel postulate." The 5th postulate actually says that in constructions of the sort shown below, if angles A+B < 180o then the lines L1 and L2 will meet on the right, but if C + D < 180o then they will meet on the left. The implication is that if, A, B, C, and D are right angles, and thus A+B = C + D = 180, then they will never meet anywhere.

For centuries people tried to derive this Axiom from the first four, thereby eliminating the need for it, but they failed repeatedly. Some actually spent their lives futilely trying. Finally, in the 19th Century, mathematicians like Lobachevski, Gauss, and Bolyai showed that in fact the 5th postulate was independent of the first 4, and there were consistent systems of geometry in which the first four were true and the 5th false.

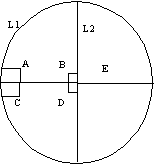
For example, consider the geometry of the surface of a sphere. Line segments can be defined to be the shortest distance between points, which on a sphere are always part of great-circle, or circumference. Consider the two lines of longitude L1 and L2 that I show below, upon which the equator E lies perpendicular. A,B,C,D are all right angles, but lines L1 and L2 meet in two places (at the poles).

Later in the century Rieman showed how to axiomatize a whole series of Geometries, one of which was Euclidean. A consequence of Euclidean geometry is that all triangles have 3 angles which sum to 180^o. The triangles on the surface of a sphere sum to more than 180, and those on a surface like a saddle to less than 180. Einstein's famous theory of General Relativity made these alternative axiomatizations of Geometry take on more importance when he conceived of space-time as having a geometry determined by the distribution of mass and energy. As it turns out, physicists now believe it is likely that Einstein is right, and the universe we happen to inhabit is Non-Euclidiean, where the sum of any three angles in a triangle made up of three lines, where a line is the shortest distance between two points, is more than 180^o.

Many theories have been axiomatized, e.g., Newton's theory of celestial mechanics, which was modeled on Euclid's Elements. A few other important theories that have been axiomatized are:

Mathematics

Geometry (Euclid 300 B.C., D. Hilbert (early 20th Century))

Arithmetic (Peano, Dedekind, 19th Century)

Set Theory (Cantor, Zermelo, Fraenkel, early 20th Century)

Probability Theory (Kolmogorov)

Science

Physics (Newton, 17th Centurys; Maxwell, Hertz, 19th Century; Hilbert, early 20th)

Social Science

Utility Theory (Von Neuman, Morgenstern, middle 20th)

Bayesian Decision Theory (Savage, middle 20th)