80-110: The Nature of Mathematical Reasoning
Spring 1998
Class 7: 2/3/98
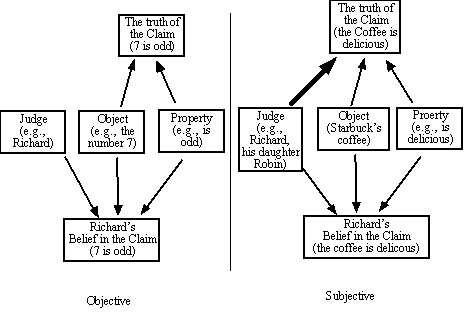
1. Subjective vs. Objective
A final criteria we want for mathematics is objectivity. It does not seem to be a matter of opinion whether 2+2=4, and it should not be a matter of opinion whether an argument is deductively valid or not, nor should it be a matter of opinion whether a mathematical object (e.g., a number) satisfies a mathematical definition, (e.g., of being rational, or odd).

Whether an object has a property is sometimes objective and sometimes subjective. The difference has to do with whether or not the subject, or judge, is essential to whether or not the object has the property. For example, the number 4 is even whether I say so or not, but the coffee on my desk is neither delicious nor undelicious all by itself. Even though it is Staruckís best roast, made within the last 15 minutes, and most coffee gourmetís would agree that it was a delicious cup of coffee, my eight year old daughter Robin and my colleague in the next office would label it on the verge of disgusting. By itself, the coffee is neither delicious nor disgusting. Oneís belief about a claim is subjective, that is, a function of who is doing the judging, but the truth of an objective claim is presumably a function of only the world, not the subject doing the judging.
The problem is that you cannot get direct access to the truth of a claim, even if it is an objective claim. You can only form beliefs about its truth. Thus, even if deductive validity is an objective concept, then we still must decide what it is about an argument that makes it valid. Which brings us to a few examples of arguments that seduce us into believing they are valid, but are in fact fallacious.
2. Fallacies & Rigor
All sorts of arguments seem compelling yet are fallacious. That is, they rely on an inference which is not truth preserving in every case, but seems to be solid. In the following example, applying what look like normal algebraic rules produces an absurd result.
Algebra
1) Assume that a = b + c.
2) (a-b)a = (a-b)(b+c) multiply both sides of 1 by (a - b)
3) a2 - ab = ab + ac - b2 - bc distribute
4) a2 - ab - ac = ab - b2 - bc substract (ac) from both sides
5) a(a - b - c) = b(a - b - c) factor each side
6) a = b divide both sides by (a - b - c)
In the right hand column I have described the justification for each step. Multiplying or dividing equals by equals should give equals. Subtracting equals from equals should give equals. Yet somehow I have proved, from a = b+c, that a=b, a patent absurdity.
The fallacy is in the final step, where I divide both sides by (a - b - c). If a = b+c, then
(a - b - c) = 0, and dividing by 0 is undefined. Dividing by 0 is involved routinely in mathematical fallacies.
A second fallacy is Zenoís famous argument that Achilles, the fastest Greek runner of his time, could not catch a tortoise in a race in which the tortoise was given a head start.
Zeno's argument is a little confusing, but the key to understanding it is to look at the picture on the top of page 23 in Glymour's chapter. Putting the line segments together end to end results in a line whose length is where Achilles catches the tortoise. If the line is infintely long, then Achilles never catches the tortoise. If Achilles could catch the tortoise, then when we put together all the line segments in the picture end to end, we would have a finite line segment. If Achilles could never catch the tortoise, the sum of these line segments (the line that would result from putting the segments together end to end) would be a line of infinite length. The fallacy in Zeno is that an infinite sum of smaller and smaller lengths cannot add up to a finite length. We now know this is false, since the sum .3 + .03 + .003 .... adds up to 1/3.
Exercises Consider the following problem. Suppose you are on a game show in which there are 3 doors, one of which will contain a terrific prize. The door that contains the prize will be decided randomly before the show, and each door has an equal chance of containing the przie. You are asked to pick a door, but you are not shown what is behind your door. To be concrete, suppose you choose door 1. Your host then shows you one of the doors you did not pick, the only restriction being that the door you are shown is empty. Say you are shown that door 2 does not have the prize. Assuming you want to maximize the chances for getting a great prize: the question is: Do you want to stay with your original pick (door 1) or switch (to door 3)? Pick one of the following answers, and justifiy your pick. Type up your answer and send it to Kevin. A) Stay with original pick (door 1 has a better chance of having the prize than door 3). B) Switch (door 3 has a better chance of having the prize than door 1). C) It doesn't matter (door 1 and door 3 have the same chance of having the prize)
Reading (none)