15-110 Principles of Computing

Summer 2017

Programming Assignment 2

Note: You are responsible for protecting your solutions to these problems from being seen by other students both physically (e.g., by looking over your shoulder) and electronically. In particular, since the lab machines use the Andrew File System to share files worldwide, you need to be careful that you do not put files in a place that is publicly accessible.

If you are doing the assignment on the Gates-Hillman Cluster machines we use in lab or on unix.andrew.cmu.edu, our recommendation is that you create a pa2 directory under ~/private/15110 for this assignment. That is, the new directory pa2 is inside a directory called 15110, which is inside the directory called private, which is inside your home directory. (Every new andrew account is set up with a private subdirectory within the account's home directory that only that account can access.) Please refer to Setting up Directories for information about managing your directories.

    Overview

    For this assignment, you will create a Python source file (that is, a text file containing Python code) for each of the problems below. You should store all of these files in a folder named pa2, which you will zip up and submit.

    As you will discover this semester, computer programs are rarely correct when they are first written. They often have bugs. In addition to writing the code, you should test your code on multiple inputs, for which you independently know the correct output (e.g., by plugging the inputs into a calculator). Don't worry about very small differences between the output of the calculator and the results of your code; these are rounding effects due to the computer's approximations for real numbers.

    Part One

    Write Python functions to calculate each formula as indicated below. Pay close attention to whether your functions should return their results or print them. You should run Python and test your functions to make sure they behave as shown in the examples. Before submitting your code, you should also download this file: test_pa2_v2.py and do the following: 

    > from test_pa2_v2 import *           (OR python3 -i test_pa2_v2.py)
>>> test_all()
    Some of the tests will print out what your program's printed output should be and ask you to visually compare. Others will automatically check that your function returns the correct value. If the printed output doesn't match, and/or you don't see the message "All tests completed", then there is something that needs to be fixed for you to get full credit. You can isolate the problem as follows: 
    >>> test_cone_volume()
Test complete
>>> test_print_object_volume()
Test complete
...
    and so forth. There is a test function for each of the functions you are to write. Please note: Passing the tests does not guarantee you full credit. In the case of printed output, you must examine the output yourself to judge whether it's correct. In addition, there may be cases not covered in the tests we give you, and there may be other requirements for your code that are stated in this assignment but not checked by the test file. It is your responsibility to think about whether your function definition satisfies the requirements.

  1. The volume of a cone can be calculated from the radius of its base (r) and its height (h) using the formula:

    \[\frac{1}{3}\pi r^2 h\]

    1. [1 point] In cone.py, write a Python function cone_volume(radius,height) that calculates and returns the volume of a cone whose base's radius is radius and whose height is height. In order to use the definition of PI (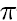), put the following line as the first line of your Python file: 

      	import math
      Use math.pi for PI (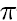) in your Python code

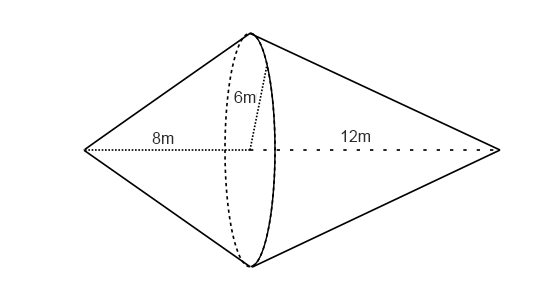
    2. [1 point] Consider the three-dimensional object shown in the figure to the right, which consists of two cones whose heights are 8m and 12m, respectively, and which share a base, whose radius is 6m.

      In cone.py, define a Python function print_object_volume() that uses cone_volume to calculate the total volume occupied by the pictured object (i.e., the total volume occupied by the two cones that make up the object). It should return None after printing the following line of text:

      The total volume of the two cones is XXXX.XXXXXXXXXXX

      (Replacing XXXX.XXXXXXXXXXX with the calculated volume.)

      Your print_object_volume() function must be defined without directly calculating the volume of the cones. Instead you must call the cone_volume function you wrote for part a.

    Example usage: 

    > from cone import *           (OR > python3 -i cone.py)
>>> cone_volume(4,10)
167.55160819145564
>>> cone_volume(4,15)
251.32741228718342
>>> print_object_volume()
The total volume of the two cones is 418.87902047863906
    Note that Python does not display None even though that is the value returned. On the other hand: 
    >>> print(print_object_volume())
The total volume of the two cones is 418.87902047863906
None

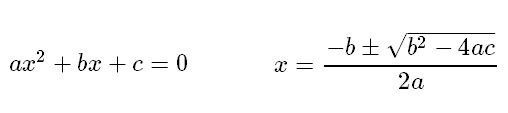
  2. [2 point] A quadratic equation ax2+bx+c=0 can be solved for x by calculating:

    In quadratic.py, define a Python function quadratic(a, b, c), which takes the constants a, b, and c and calculates and prints the two values of x for which the equation holds, using exactly the same format as shown in the examples below. You may assume that b2−4ac is non-negative, and the function should output the same solution twice when b2−4ac=0. (The function should always return None, so there's no need for a return statement.) You will need to import the math library again in this file. Beware formatting! Don't let extra spaces appear. You'll need to use sep= or end= in your call to print.

    Example usage:

    > from quadratic import *           (OR > python3 -i quadratic.py)
>> quadratic(1.0, 3.0, -4.0)
[x1: 1.0, x2: -4.0]
>> quadratic(1, 4, 4)
[x1: -2.0, x2: -2.0]
>>

    3. Part Two

    These problems require you to write programs that do more than implement mathematical formulas.

  3. [2 points] Consider a cubic polynomial function of the form:

    \[f(x) = ax^3 + bx^2 + cx + d.\]

    In list_cubic.py, define a Python function list_cubic(a, b, c, d) that prints a list of the values of \(f(x)\) for integer \(x = 0\) to \(x = 20\) (inclusive), given the coefficients of the polynomial in the order shown. Your function must use a loop; do not repeat the code for the calculation 21 times! (The function should always return None, so there's no need for a return statement.)

    For example, if your polynomial is \(f(x) = 3x^3 + 4x^2 - 3x + 2,\) then the output would look like: 

    > from list_cubic import *           (OR > python3 -i list_cubic.py)
>>> list_cubic(3, 4, -3, 2)
2
6
36
110
...
25542
>>>

    Be sure to test your function using a few more polynomials besides this one to be more confident that your function is correct. Use a calculator to check the first few values in the sequence as well as the last one.

  4. One way to use the modulo operator (in Python, the percent sign %) and integer division operator (double slash //) is to manipulate the individual digits of a number. Notice the following facts about integer division and modular arithmetic using the modulus 10:

    For this problem you are to use this information to write three functions. Define them in the file digit.py:

    1. [1 point] Write a Python function called digit(num, pos) in the file digit.py that takes in any positive integer num and the position of the desired digit pos and returns the digit in the desired position. Assume that the function will always be called with a value for pos that is greater than zero and no larger than the number of digits in num. Furthermore, assume that a pos of 1 indicates the rightmost digit, a pos of 2 indicates the digit second from the right and so on.

      Example usage:

      > from digit import *           (OR > python3 -i digit.py)
>> digit(73, 1)
3
>> digit(9824759837450, 8)
5
>>

    2. [2 points] In the same file (digit.py), write another function called reverse_num(num, num_digits) that takes in any positive integer num and its length, and uses the function digit to compute and return the positive integer with the same digits but in the reverse order. You can assume that the function will always be called with a positive integer and that the correct length will be supplied. If num ends with one or more 0 digits, the output (of course!) will be a number with fewer digits, since Python doesn't display leading 0 digits. For any credit, you must call the function digit in this function!

      Example usage:

      > from digit import *           (OR > python3 -i digit.py)
>>> reverse_num(987654321, 9)
123456789
>>> reverse_num(20, 2)
2
>>> reverse_num(200, 3)
2
>>> reverse_num(2000, 4)
2
    3. [1 point] We consider an integer to be a palindrome if it reads the same forwards and backwards. Again in the file digit.py, write a function pal_num(num, num_digits)that returns a Boolean value, True if the given number is a palindrome and False otherwise. Note that you can return a Boolean value just like any other value. For instance, the following is a Python function that always returns True (try it and see!): 
      def taut(n):
    return n == n
      For any credit, you must call the function reverse_num in this function.

      Example usage:

      > from digit import *           (OR > python3 -i digit.py)
>>> pal_num(9876789, 7)
True
>>> pal_num(98767890, 8)
False
      If we add a number to its reversed version, we often get a palindrome (why wouldn't we?): 
      >>> pal_num(1234 + reverse_num(1234, 4), 4)
True
>>> pal_num(5678 + reverse_num(5678, 4), 4)
False
>>> 5678 + reverse_num(5678, 4)
14443
>>> 14443 + reverse_num(14443, 5)
48884
>>> pal_num(48884, 5)
True

      4. Submission

      You should now have a pa2 directory that contains the files cone.py, quadratic.py, list_cubic.py and digit.py. Zip up your directory and hand it in.