15-110 Lab Exam 2 Practice Problems

Lab Exam 2 Practice Problems

The problems are not in order of difficulty. If you get stuck on a problem, try the next one.

Recursion

Write a function f1(list) that returns the sum of the elements in the list.

>>> f1([1,2,3,4])
10
>>> f1([])
0

Show Solution

def f1(list):  
    if list == []:
        return 0
    return list[0] + f1(list[1:])

Consider the following function:

\( f(n) = \begin{cases} n//2 & \text{if n is even} \\ 3n+1 & \text{if n is odd} \\ \end{cases} \)
Write a function f2(n) that returns the number of steps of the function \(f(n)\) until it reaches 1 (this is also known as the Collatz Conjecture). For example, consider \(f(6): 6 \rightarrow 3 \rightarrow 10 \rightarrow 5 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1\), since there are a total of 9 steps, f2(6) evaluates to 9.
```
>>> f2(1)
1
>>> f2(6)
9
>>> f2(11)
15
>>> f2(637228127)
276
```
Show Solution
```
def f2(n):
    if n == 1:
        return 1
    if n % 2 == 0:
        return 1 + f2(n//2)
    else:
        return 1 + f2(3*n+1)
```

Write a function f3(list) that prints out the elements in the list in reverse order.

>>> f3([1,2,3])
3
2
1
>>> f3([])
>>> f3([3,2,1])
1
2
3

Show Solution

def f3(list):  
    if list == []:
        return
    f3(list[1:])
    print(list[0])

Write a function f4(list) that multiplies all of the odd elements in the list by 3 and prints out each tripled element.

>>> f4([1,2,3,4])
3
9
>>> f4([2,4])
>>> f4([11,42,63,15])
33
189
45

Show Solution

def f4(list):  
    if list == []:
        return
    if list[0] % 2 == 1:
        print(3*list[0])
    f4(list[1:])

Write a function f5(list) that multiplies all of the odd elements in the list by 3 and prints out each element of the modified list in reverse order.

>>> f5([1,2,3,4])
4
9
2
3
>>> f5([2,4])
4
2
>>> f5([11,42,64,15])
45
64
42
33

Show Solution

def f5(list):  
    if list == []:
        return
    f5(list[1:])
    if list[0] % 2 == 1:
        print(3*list[0])
    else:
        print(list[0])

Write a function f6(lst) that takes any multidimensional list and returns a one dimensional list with the same values. This is also known as flattening a list. Remember that you can use type([1,2,3]) == list to determine if something is a list. There should be one base case and two recursive cases.
```
>>> f6(['baa'])
['baa']
>>> f6(['baa', [4, True, [10, 5], [1, 2, ['moo']]], ["chirp"]])
['baa', 4, True, 10, 5, 1, 2, 'moo', "chirp"]
>>> f6([])
[]
>>> f6([[[[[[[[[[[[[[23]]]]]]]]]]]]]])
[23]
```
Show Solution
```
def f6(lst):  
    if type(lst) != list or lst == []:
        return lst
    elif type(lst[0]) != list:
        return [lst[0]] + f6(lst[1:])
    else:
        return f6(lst[0]) + f6(lst[1:])
```
Consider a function \(L_n\):

\( L_n = \begin{cases} 2 & \text{if } n = 0; \\ 1 & \text{if } n = 1; \\ L_{n-1}+L_{n-2} & \text{if } n > 1; \\ \end{cases} \)
Write a function f7(n) that calculates \(L_n\)
```
>>> f7(3)
4
>>> f7(14)
843
>>> f7(0)
2
>>> f7(22)
39603
```
Show Solution
```
def f7(n):  
    if n == 0:
        return 2
    if n == 1:
        return 1
    return f7(n-1) + f7(n-2)
```

Write a function f8(s) that returns True if s is a palindrome, and False otherwise.

>>> f8("")
True
>>> f8("kayak")
True
>>> f8("penguin")
False
>>> f8("a")
True

Show Solution

def f8(s):  
    if s == "":
        return True
    if s[0] == s[-1]:
        return f8(s[1:-1])
    return False

Write a function f9(n) that returns \(n!\)

>>> f9(0)
1
>>> f9(1)
1
>>> f9(2)
2
>>> f9(3)
6

Show Solution

def f9(n):  
    if n == 0:
        return 1
    return n * f9(n-1)

Write a function f10(list) that returns len(list).

>>> f10([1,2,3])
3
>>> f10([])
0
>>> f10([2])
1

Show Solution

def f10(list): 
    if list == []:
        return 0
    return 1 + f10(list[1:])

Write a function f11(list) that returns the last element in the list.

>>> f11([1,2,3])
3
>>> f11([])
>>> f11([1])
1

Show Solution

def f11(list): 
    if list == []:
        return None
    if len(list) == 1:
        return list[0]
    return f11(list[1:])

Write a function f12(n) that prints the numbers n through 1 in descending order.

>>> f12(3)
3
2
1
>>> f12(0)
>>> f12(1)
1

Show Solution

def f12(n): 
    if n > 0:
        print(n)
        f12(n-1)

Write a function f13(n) that returns the number of digits in n. You may assume n is a positive integer.
```
>>> f13(9175)
4
>>> f13(34)
2
>>> f13(268)
3
>>> f13(0)
1
```
Show Solution
```
def f13(n):
    if n < 10:
        return 1
    return 1 + f13(n//10) 
```

Write a function f14(list) that returns the first odd number in the list, and None if there are no odd numbers in the list.

>>> f14([1,2,3])
1
>>> f14([2,4])
>>> f14([2,4,6,8,10,3])
3

Show Solution

def f14(list):
    if list == []:
        return None
    if list[0] % 2 == 1:
        return list[0]
    return f14(list[1:])

Write a function f15(list) that returns the sum of all the odd numbers in the list.

>>> f15([1,2,3])
4
>>> f15([2,4])
0
>>> f15([1,3,6,9])
13

Show Solution

def f15(list):
    if list == []:
        return 0
    if list[0] % 2 == 1:
        return list[0] + f15(list[1:])
    return f15(list[1:])

Write a function f16(list) that returns a list of all the odd numbers in the list.

>>> f16([1,3,5,7])
[1, 3, 5, 7]
>>> f16([2,4])
[]
>>> f16([1,2,3,4,5])
[1, 3, 5]

Show Solution

def f16(list):
    if list == []:
        return []
    if list[0] % 2 == 1:
        return [list[0]] + f16(list[1:])
    return f16(list[1:])

Write a function f17(list) that returns the second to last element in the list. Assume len(list) > 1.

>>> f17([1,2])
1
>>> f17([1,2,3,4])
3
>>> f17([1,2,3])
2

Show Solution

def f17(list):
    if len(list) == 2:
        return list[0]
    return f17(list[1:])

Write a function f18(a,b) that returns the greatest common divisor of a and b.

>>> f18(5,4)
1
>>> f18(40,60)
20
>>> f18(9,3)
3

Show Solution

def f18(a,b):  
    if b == 0:
        return a
    return f18(b, a%b)

Write a function f19(list1, list2) that merges list1 and list2 in ascending order. Assume list1 and list2 are already sorted.

>>> f19([1,2,3],[4,5])
[1, 2, 3, 4, 5]
>>> f19([4,5],[1,2,3])
[1, 2, 3, 4, 5]
>>> f19([],[1,2,3])
[1, 2, 3]
>>> f19([1,2,3],[])
[1, 2, 3]
>>> f19([], [])
[]

Show Solution

def f19(list1, list2):
    if list1 == []:
        return list2
    if list2 == []:
        return list1
    if list1[0] < list2[0]:
        return [list1[0]] + f19(list1[1:], list2)
    return [list2[0]] + f19(list1, list2[1:])

Write a function f20(list) that mergesorts the list. Consider using

f19(list1,
                    list2)

for the merging step.

>>> f20([3,2,1])
[1, 2, 3]
>>> f20([])
[]
>>> f20([5,3,1,2,4,6])
[1, 2, 3, 4, 5, 6]

Show Solution

def f20(list):
    if len(list) <= 1:
        return list
    else:
        mid = len(list)//2
        list1 = f20(list[:mid])
        list2 = f20(list[mid:])
        return f19(list1, list2)

Write a function f21(tree) that returns the height of the tree. The tree has the structure [value, left subtree, right subtree].

>>> f21([])
0
>>> f21([1,[],[]])
1
>>> f21([1,[1,[],[]],[]])
2

Show Solution

def f21(tree):
    if tree == []:
        return 0
    return 1 + max(f21(tree[1]), f21(tree[2]))

Write a function f22(tree) that returns the number of nodes in the tree. The tree has the structure [value, left subtree, right subtree].

>>> f22([])
0
>>> f22([1,[],[]])
1
>>> f22([1,[1,[],[]],[1,[],[]])
3

Show Solution

def f22(tree):
    if tree == []:
        return 0
    return 1 + f22(tree[1]) + f22(tree[2])

Write a function f23(tree) that returns the sum of the nodes in the tree. The tree has the structure [value, left subtree, right subtree].

>>> f23([])
0
>>> f23([1,[],[]])
1
>>> f23([1,[2,[],[]],[3,[],[]])
6

Show Solution

def f23(tree):
    if tree == []:
        return 0
    return tree[0] + f23(tree[1]) + f23(tree[2])

Write a function f24(tree) that prints out the values of the tree in ascending order. The tree has the structure [value, left subtree, right subtree] and is a binary search tree.
```
>>> f24([])
>>> f24([1,[],[]])
1
>>> f24([2,[1,[],[]],[3,[],[4,[],[]]])
1 
2 
3 
4
```
Show Solution
```
def f24(tree):
    if tree == []:
        return
    f24(tree[1])
    print(tree[0])
    f24(tree[2])
```
Write a function f25(tree) that returns the smallest element in the tree. The tree has the structure [value, left subtree, right subtree] and is a binary search tree. Return -1 if the tree is empty.
```
>>> f25([])
-1
>>> f25([1,[],[]])
1
>>> f25([2,[1,[],[]],[3,[],[4,[],[]]])
1
```
Show Solution
```
def f25(tree):
    if tree == []:
        return -1
    if tree[1] == [] and tree[2] == []:
        return tree[0]
    return f25(tree[1])
```

Looping

Write a function f1(n) that prints the following triangle.

>>> f1(5)
1
1 2
1 2 3
1 2 3 4
1 2 3 4 5
>>> f1(0)
>>> f1(1)
1

Show Solution

def f1(n):  
    for i in range(n):
        for j in range(i+1):
            print(j+1, end=" ")
        print()

Write a function f2(n) that prints the following triangle.

>>> f2(3)
1
2 3
4 5 6
>>> f2(0)
>>> f2(1)
1
>>> f2(5)
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15

Show Solution

def f2(n):  
    count = 1
    for i in range(n):
        for j in range(i+1):
            print(count, end=" ")
            count = count + 1
        print()

Write a function f3(n) that prints the following triangle.

>>> f3(3)
1
2 3
4 5 6
2 3
1
>>> f3(4)
1
2 3
4 5 6
7 8 9 10
4 5 6
2 3
1
>>> f3(0)
>>> f3(1)
1

Show Solution

def f3(n):  
    count = 1
    for i in range(n):
        for j in range(i+1):
            print(count, end=" ")
            count = count + 1
        print()
    for i in range(n-1):
        count = count - (2*(n-i-1)+1)
        for j in range(n-i-1):
            print(count, end=" ")
            count = count + 1
        print()

Write a function f4(n) that prints the following triangle.

>>> f4(3)
1
2 3
4 5 6
7 8
9
>>> f4(0)
>>> f4(1)
1

Show Solution

def f4(n):  
    count = 1
    for i in range(n):
        for j in range(i+1):
            print(count, end=" ")
            count = count + 1
        print()
    for i in range(n-1):
        for j in range(n-i-1):
            print(count, end=" ")
            count = count + 1
        print()

Write a function f5(matrix) that prints the sum of every row in the matrix.

>>> f5([[1,0],[0,1]])
1
1
>>> f5([[1,2,3],[4,5,6]])
6
15
>>> f5([[1],[2],[3],[4]])
1
2
3
4

Show Solution

def f5(matrix):  
    for i in range(len(matrix)):
        sum = 0
        for j in range(len(matrix[i])):
            sum = sum + matrix[i][j]
        print(sum)

Write a function f6(matrix) that returns the sum of all the elements in the matrix.

>>> f6([[1,0],[0,1]])
2
>>> f6([[1,2,3],[4,5,6]])
21
>>> f6([[1],[2],[3],[4]])
10

Show Solution

def f6(matrix):  
    sum = 0
    for i in range(len(matrix)):
        for j in range(len(matrix[i])):
            sum = sum + matrix[i][j]
    return sum

Write a function f7(matrix) that returns the product of all the elements in the matrix.

>>> f7([[1,0],[0,1]])
0
>>> f7([[1,2,3],[4,5,6]])
720
>>> f7([[1],[2],[3],[4]])
24

Show Solution

def f7(matrix):  
    prod = 1
    for i in range(len(matrix)):
        for j in range(len(matrix[i])):
            prod = prod * matrix[i][j]
    return prod

Write a function f8(matrix) that will print the odd numbers in the matrix with each row on one line.

>>> f8([[1,0],[0,1]])
1
1
>>> f8([[1,2,3],[4,5,6]])
1 3
5
>>> f8([[1],[2],[3],[4]])
1

3

Show Solution

def f8(matrix):  
    for i in range(len(matrix)):
        for j in range(len(matrix[i])):
            if matrix[i][j] % 2 == 1:
                print(matrix[i][j], end=" ")
        print()

Write a function f9(matrix1, matrix2) that will return the sum of matrix1 and matrix2. Assume matrix1 and matrix2 have the same dimensions.

>>> f9([[1,0],[0,1]],[[1,0],[0,1]])
[[2, 0], [0, 2]]
>>> f8([[1,2,3],[4,5,6]],[[-1,-1,-1],[-1,-1,-1]])
[[0, 1, 2], [3, 4, 5]]
>>> f15([[1],[2],[3],[4]],[[4],[3],[2],[1]])
[[5], [5], [5], [5]]

Show Solution

def f9(matrix1, matrix2):
    res = []
    for i in range(len(matrix1)):
        row = []
        for j in range(len(matrix1[i])):
            row.append(None)
        res.append(row)  
    for i in range(len(matrix1)):
        for j in range(len(matrix1[i])):
            res[i][j] = matrix1[i][j] + matrix2[i][j]

Write a function f10(matrix1, matrix2) that will return the product of matrix1 and matrix2. Assume len(matrix1) == len(matrix2[0]).

>>> f10([[1,0],[0,1]],[[1,0],[0,1]],)
[[1, 0], [0, 1]]
>>> f10([[1,2,3],[4,5,6]],[[-1,-1],[-1,-1],[-1,-1]])
[[-6, -6], [-15, -15]]
>>> f10([[4,3,2,1]],[[1],[2],[3],[4]])
[20]

Show Solution

def f10(matrix1, matrix2):  
    res = []
    for i in range(len(matrix1)):
        row = []
        for j in range(len(matrix2[0])):
            row.append(0)
        res.append(row)
    
    for i in range(len(matrix1)):
        for j in range(len(matrix2[0])):
            for k in range(len(matrix1[0])):
                res[i][j] = res[i][j] + matrix1[i][k] * matrix2[k][j]
    
    return res

Write a function f11(matrix) that returns True if the matrix is the identity matrix, and False otherwise. Assume

len(matrix) ==
                    len(matrix[0])

>>> f11([[1]])
True
>>> f11([[1,0,0],[0,1,0],[0,0,1]])
True
>>> f11([[1,0,0],[0,1,5],[0,0,1]])
False

Show Solution

def f11(matrix):  
    for i in range(len(matrix)):
        for j in range(len(matrix[i])):
            if i == j and matrix[i][j] != 1:
                return False
            if i != j and matrix[i][j] != 0:
                return False
    return True

Write a function f12(rows, cols) that returns a two dimensional list where each element corresponds to how many adjacent neighbors it has. Neighbors are defined as spaces above, below, to the left, and to the right.

>>> f12(3,3)
[[2, 3, 2], [3, 4, 3], [2, 3, 2]]
>>> f12(5,1)
[[1], [2], [2], [2], [1]]
>>> f12(5,0)
[[], [], [], [], []]
>>> f12(0,5)
[]
>>> f12(2,2)
[[2, 2], [2, 2]]

Show Solution

def f12(rows, cols):
    matrix = []
    for i in range(rows):
        row = []
        for j in range(cols):
            row.append(0)
        matrix.append(row)

    for row in range(rows):
        for col in range(cols):
            num_neighbors = 0
            if (row - 1) in range(rows):
                num_neighbors += 1
            if (row + 1) in range(rows):
                num_neighbors += 1
            if (col - 1) in range(cols):
                num_neighbors += 1
            if (col + 1) in range(cols):
                num_neighbors += 1
            matrix[row][col] = num_neighbors
    return matrix

Canvas

Write a function f1(matrix) that draws 80x60 rectangles for each element in the two dimensional matrix. The rectangles should be colored blue if the element is even, and yellow otherwise.

>>> f1([[1, 0], [0, 1], [1, 0], [0, 1]])

>>> f1([[0,2,1,4], [4,5,3,8], [9,4,7,1], [5,1,7,0]])

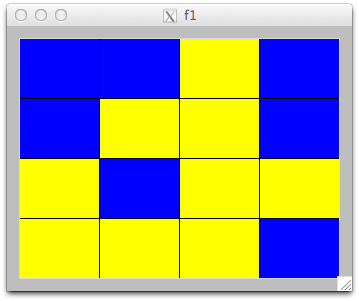
>>> f1([[7, 4, 2, 3, 1, 3, 8, 9]])

Show Solution

import tkinter
from tkinter import Canvas

def f1(matrix):
    num_rows = len(matrix)
    num_cols = len(matrix[0])
    rect_width = 80
    rect_height = 60
    my_window = tkinter.Tk()
    my_canvas = Canvas(my_window, width = num_cols*rect_width, height = num_rows*rect_height)
    my_canvas.pack()

    colors = ["blue", "yellow"]
    for row in range(num_rows):
        for col in range(num_cols):
            my_canvas.create_rectangle(col*rect_width, row*rect_height,
                                       col*rect_width + rect_width,
                                       row*rect_height + rect_height,
                                       fill = colors[matrix[row][col] % 2])

Write a function f2() that draws the picture below on a 400x400 window. The radius of the larger red circle is 100 units, the radius of the inner white circle is 75 units, and the radius of the inner red circle is 30 units. The circles are all positioned at the center of the windows.

Show Solution

import tkinter
from tkinter import Canvas

def f2():
    my_window = tkinter.Tk()
    my_canvas = Canvas(my_window, width = 400, height = 400)
    my_canvas.pack()
    my_canvas.create_rectangle(0,0,400,400,fill='white')
    my_canvas.create_oval(100,100,300,300,fill='red')
    my_canvas.create_oval(125,125,275,275,fill='white')
    my_canvas.create_oval(170,170,230,230,fill='red')

Write a function f3(width, height), that takes a width and height and recursively draws rectangles, where the first rectangle is the size of the canvas and each consecutive rectangle has the same width but has a height that is exactly 7/8 the size of the previous heightt. The function should stop drawing once the height is less than 5. You will most likely need a helper function

>>> f3(400, 400)

Show Solution

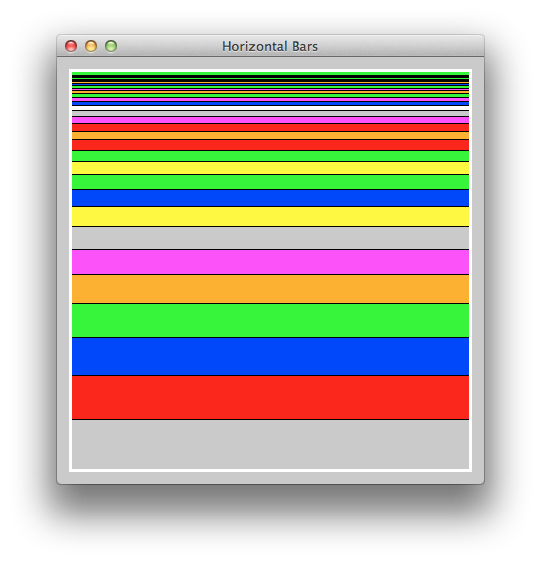
import tkinter
from tkinter import Canvas
from random import randint

def f3(width, height):
    my_window = tkinter.Tk()
    my_canvas = Canvas(my_window, width = width, height = height)
    my_canvas.pack()
    # can input any arbitrary color at first
    f3_helper(my_canvas, width, height, "white") 

def f3_helper(my_canvas, width, height, last_color):
    if height < 5:
        return None
    else:
        colors = ["red", "orange", "yellow", "green", "blue", "magenta",
                  "white", "grey"]
        fill_color = colors[randint(0, len(colors) - 1)]
        while fill_color == last_color: #this prevents repetition of colors
            fill_color = colors[randint(0, len(colors) - 1)]
        my_canvas.create_rectangle(1, 1, width, height, fill = fill_color)
        f3_helper(my_canvas, width, 7*height/8, fill_color)