SEMITIP V6, Uni2, Example 4: undoped semiconductor, with no surface states
Click here for input/output files for Example 4
This example illustrates a band bending computation for an undoped semiconductor, assuming dielectric constant of 16.3 (as appropriate to Ge) and a band gap of 2 eV. A sample voltage of +3 V is applied. The resultant band bending is about 0.87 eV. Output to FORT.11 gives the electrostatic potential energy (column 2) along the central axis vs. the z-distance through the vacuum and semiconductor (column 1). Output to FORT.12 gives the electrostatic potential energy on the surface (column 2) vs. the radial distance along the surface (column 1). When plotted, these potentials appear as:
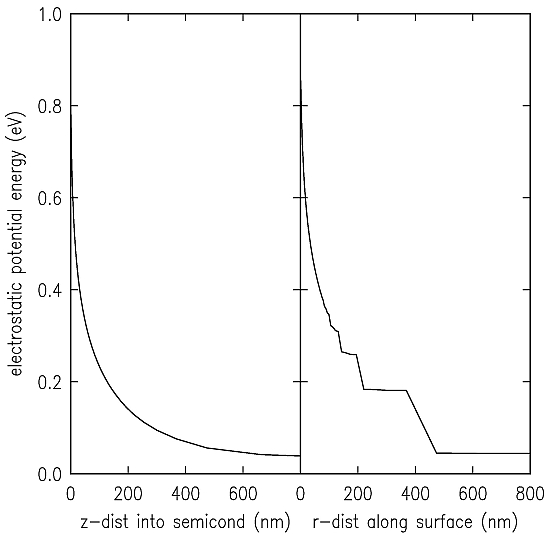The irregular behavior of the potential seen at large distances, particularly for the radial direction, can be eliminated by tightening the convergence parameters in the calculation. It should be noted that the results of these sort of computations for undoped semiconductors can depend on the grid size and boundary condition used. For example, in the present case if we use Von Neumann boundary conditions (see discussion of
Boundary Conditions), then the band bending result increases to 0.93 eV. This discrepancy is even worse for lower dielectric constants (e.g. as occur for GaAs). It is difficult to definitely determine the band bending for undoped semiconductors, although, in nearly all physical cases, there will be something that constrains the band bending (such as residual doping, or extrinsic surface states, or an adjoining doped layer) and so this situation of a perfect, undoped semiconductor will not usually be encountered in experiment.