SEMITIP V6, Uni2, Example 1: n-type GaAs(110)

Click here for input/output files for Example 1

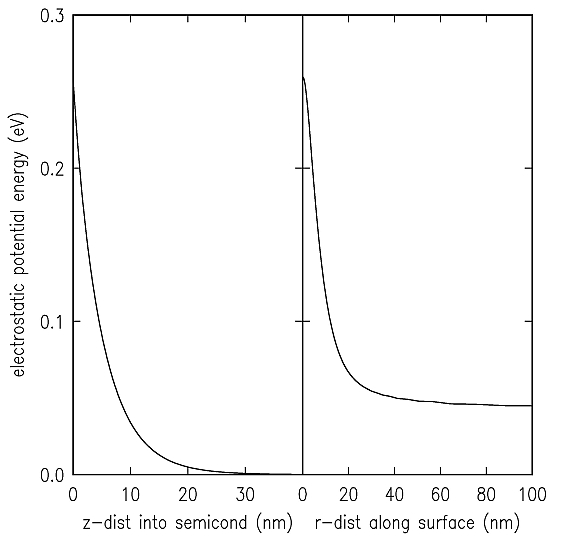
This example illustrates a simple band bending computation for n-type GaAs doped at 1018 cm-3, assuming a tip radius of 10 nm, contact potential of 0 eV, and a sample-tip voltage of 1 V. The semiconductor is thus in depletion. Intrinisic surface states are present just above the conduction band edge (lines 21-24 of the FORT.9 input file), but they play little role in the solution. Output to FORT.11 gives the electrostatic potential energy (column 2) along the central axis vs. the z-distance through the vacuum and semiconductor (column 1). Output to FORT.12 gives the electrostatic potential energy on the surface (column 2) vs. the radial distance along the surface (column 1). When plotted, these potentials appear as:

We see that only about a quarter of the applied voltage bias is dropped in the semiconductor, considerably smaller than occurs for the analogous one-dimensional case as in Example 1 of Uni1. Also note that the electrostatic potential at the surface does not fall to zero even for large radial distance from the central axis. This is because intrinsic surface states are included; those distributions are located predominantly above the conduction band edge, but with weak Gaussian tails extending down into the band gap region. The density of surface states in those talks is sufficient to produce a small amount of depletion of the semiconductor even far from the tip. (If these states are removed, e.g. by setting the state density on line 21 of FORT.9 to be zero, then this depletion is eliminated and the potential falls to zero far from the tip).

Contour lines for the potential from FORT.20 - FORT.26 are shown below, plotted over a horizontal distance of 10 nm and a vertical distance of 10 nm.

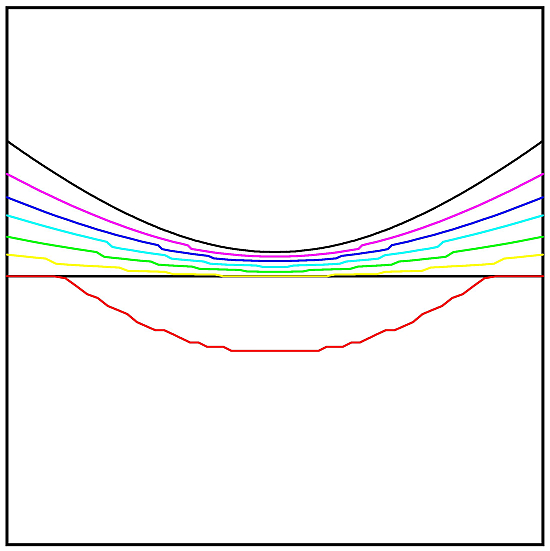
The spacing of the contour lines is deduced from the last few lines of the FORT.16 file: 
 MIN, MAX POTENTIAL VALUES = -3.29192517E-07   1.0000000    
 CONTOUR SPACING =  0.14285719
The sample bias voltage in this example is 1.0 V and the contact potential is 0.0 eV. Thus, the electrostatic potential of the tip relative to a point deep inside the semiconductor is 1.0 + 0.0 = 1.0 eV. This is the maximum potential in the problem, corresponding to the surface of the tip (shown black in the above plot). Six additional potential contours (as specified in the FORT.9 file) are plotted, the first at 0.0+0.1428 eV and each successive one spaced a further 0.1428 eV from the previous.