"Evanescent" means "tending to vanish", which is appropriate because the intensity of evanescent waves decays exponentially (rather than sinusoidally) with distance from the interface at which they are formed. Evanescent waves are formed when sinusoidal waves are (internally) reflected off an interface at an angle greater than the critical angle so that total internal reflection occurs.
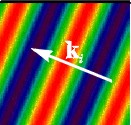
The colors in the image at right indicate the instantaneous electric field magnitude of the incident light. In this view, the plane of the page is the plane of incidence (contains the wave vector ki and the normal to the interface, the latter indicated by the black line). Surfaces on which the electric field magnitude is uniform are planes normal to the wave vector ki. Hence the incident light is a linearly polarized plane wave (LPPW). As time progresses, these planes move at the speed of light in a direction given by the wave vector ki. A LPPW is the type of wave produced by a laser.
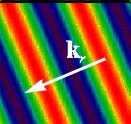
The next image at right shows the reflected wave, which is also a LPPW. The direction of the wave vector kr is determined such that the angle of incidence equals the angle of reflection.
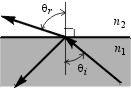
A wave (called the refracted wave) also arises on the other side of the interface where the reflection occurs. The three arrows in the sketch at left represent the 3 wave vectors for the incident, reflected and refracted waves. All 3 wave vectors lie in the same plane (the plane of incidence). The angle of incidence qi and the angle of refraction qr are related by Snell's law:
![]()
where n1 and n2 are indexes of refraction on either side of the interface. When n1 < n2 Snellís law predicts that the refracted wave vector will be bent toward to the normal. This is called an external reflection because it often occurs when the incident light strikes the outside surface of a solid object. External reflections of LPPW's always produce a refracted wave which is also a LPPW. Our interest is in internal reflections.
When n1 > n2, Snellís law (see equation above) predicts that the refracted ray is bent away from the normal as shown in the B&W sketch above (which defines qi and qr); in other words, qr > qi. This is an internal reflection. As the angle of incidence is increased, the wave vector of the refracted wave eventually becomes parallel to the interface (i.e. sinqr = 1) at one particular angle of incidence, called the critical angle:
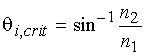
which equals about 61į at our glass/water interface. If qi > qi,crit the refracted ray disappears and the incident light undergoes total internal reflection. Although no net energy is transferred to the water under conditions of total internal reflection, an optical disturbance occurs in the water which takes the form of an "evanescent wave".
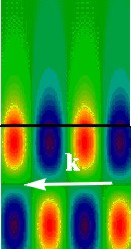
The figure at right shows the sum of the incident and reflected waves (from the two colored figures above) in the lower half. Notice that by adding the two LPPWs, we obtain a different type of wave. This wave propagates parallel to the interface as indicated by the white arrow. Click here (caution: this downloads a 2.3Mb AVI file) to view a animation of the motion of these waves.
In the upper half of the figure at right is the evanescent wave. It also propagates in the direction of the arrow at the same speed as wave below the interface. Notice how the colors in the top half all tend to green "far" above the interface (the black line in the middle): a green color denotes zero intensity (red is positive, blue is negative). Instead of varying sinusoidally with distance in all directions (like the incident wave), the electric field associated with an evanescent wave decays exponentially with distance from the interface. Under the conditions of this simulation, the electric field drops by a factor of e (=2.71) for each 260 nm increase in distance from the interface. The scale of all these colored sketches is such that the wavelength of the incident light (produced by a HeNe laser in glass) is 410 nm: this is the distance between two parallel red stripes in the incident LPPW.
Even more important (because it is what is measured by light scattering experiments) is the intensity of the light, which is proportional to the square of the electric field. The intensity drops by a factor of e for each 130 nm increase in distance from the interface. Thus only water very near the interface is illuminated by the evanescent wave. When a micron-sized particle in the water settles very close to the interface at which the evanescent wave is generated, it scatters some of the energy of the evanescent wave. This is the basis of Total Internal Reflection Microscopy.