So far, we have learned the formal syntax of the language of sentential logic, but as yet, we have talked only informally about how to interpret and evaluate its formulae.

For our logical purposes we make two idealizations: first, that atomic formulae are either true or false;

Second, that the truth-values of the atomic formulae are given by a truth-value assignment. The logical connectives are understood truth-functionally, which means that the truth-value of a compound formula is treated as a function of the truth-values of its subformulae. Given a truth-value assignment, we can thus determine the truth-value of any formula of the language relative to that assignment.

These are the fundamentals of the semantics for the language of sentential logic. They are put to work in the various tools and techniques we introduce for the evaluation of individual formulae and of inferences.

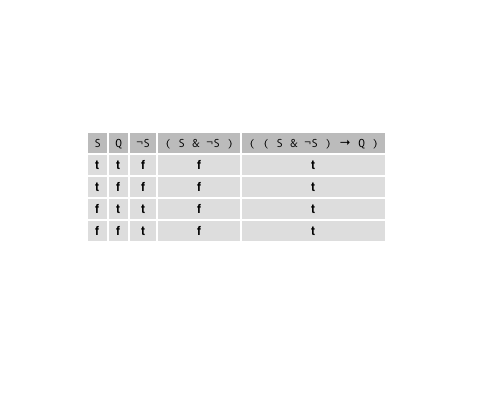
The first such tool is the truth-table. Truth-tables make it easy to investigate the semantic properties of an individual formula, to compare formulae, and to investigate the semantic properties of inferences, such as validity. This truth-table, for example, shows that a conditional whose antecedent is a contradiction is always true, a property we note by calling such a formula a tautology.

We'll learn how to use truth-tables to identify valid and invalid arguments, and also to identify or even construct counterexamples to invalid arguments as a means of demonstrating that they are indeed invalid. In addition to truth-tables, we'll also introduce truth-trees as a semantic tool. Truth-trees are, among other things, an excellent means for finding counterexamples. We will, of course, look at why the construction of such trees has a semantic motivation.

Studying this chapter will enable you first of all to explain what a truth-value assignment is.

Next you'll learn the truth-conditions for the connectives.

These two things will allow you to determine the truth-value of any formula relative to a given truth-value assignment.

You'll also learn how to construct truth-tables and use them to analyze formulae and inferences.

We'll also discuss the semantic properties of both formulae

and of arguments.

Finally, you'll learn how to construct truth-trees and use them to find counterexamples to invalid arguments.