S.
Klepper, Economics 73-100, Fall 2009
Solutions to Exam II
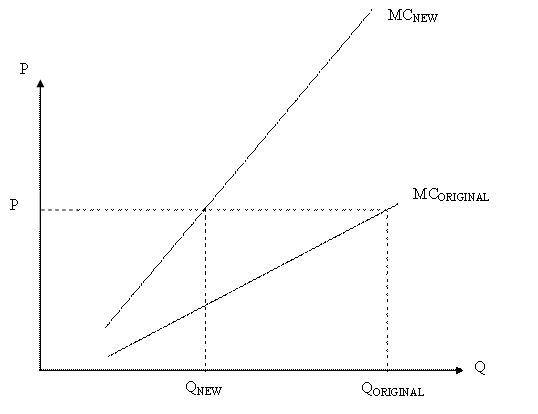
1. The marginal cost of production must be twice as great in the new plant as the original one at every level of output.† This is pictured in the figure below.† The average total cost curve is not drawn, but since the two plants have the same fixed cost the average total cost of the new plant will be greater than, but not double, the average total cost of the original plant at every level of output.†
The figure indicates the amount of output that would be produced in each plant at a hypothetical price P assuming the price is greater than the minimum average variable cost of both plants.† Both plants will produce a level of output such that the marginal cost of the marginal unit equals price.† Therefore, the marginal cost of the marginal unit of output will be the same in the two plants.† Since labor is the only variable input then the amount of labor used to produce the marginal unit of output in the two plants must be the same.
Output will be always be greater in the original plant because it has a lower marginal cost at every level of output.† If the same amount of output were produced in the two plants, then the new plant would employ twice as much labor as the original plant.† However, with output greater in the original plant than the new one, the new plant would not employ twice as much labor as the original plant.† Hence the amount of labor employed in the original plant would be more than 50% of the amount of labor employed in the new plant.
With variable costs higher at every level of output in the new plant than the original plant, the average variable cost is higher at every level of output in the new plant than the original plant.† Consequently, the break-even price would be higher in the new plant than the original plant, and it would be shut down first as the price of oil fell.† Note that if the producer had not opened the new plant, it could not have doubled its output by doubling the labor force in the original plant because production would be subject to diminishing returns.
 †
†
Based on this discussion, the answers to the
individual questions, with points allotted to the questions, are:
[4]
1. True
[4]
2. False
[5]
3. False
[5]
4. True
[6]
5. True
[6]
6. True
[6]
7. True
[6]
8. False
2. The technological breakthrough would cause the points defining level 1 to be (1,72), (2,54), (3,39), (4,27), (5,18), (6,10.8),(7,6.6), (8,3.6), (9,1.8), (10,1.5), and (11,1.35).† The willingness to pay at each point for the next unit of good X equals the number of units of good Y that could be given up for the additional unit of good X and still remain at level 1. For example, if the consumer were at the point (1,72) and got a second unit of good X, then the consumer could give up 18 units of good Y and remain on level 1 as the consumer would move to the point (2,54).† So the consumerís willingness to pay for the second unit of good X would be 18 units of good Y, which is 60% of the consumerís willingness to pay for the second unit of good X in the version of the experiment conducted in class.† Similarly, the consumerís willingness to pay for each unit of good X along level 1 would be 60% as much as in the version of the experiment conducted in class.†
The number of units of good Y the consumer would have to pay for a unit of good X would be the same in every round as in the version of the experiment conducted in class as the prices of good X and good Y would be the same in every round as the version of the experiment conducted in class.† However, if the consumerís willingness to pay for each unit of good X were 60% as much as in the version of the experiment conducted in class, then in each round of the experiment the consumer would want to choose a point on level 1 with less than or equal to the amount of good X than in the version of the experiment conducted in class.† For example, consider round 1 in which the price of good X was $3 and the budget was $90.† The consumerís willingness to pay for the eighth unit of good X after the technological breakthrough would be 3 units of good Y and thus the consumer would optimally choose the point (8,3.6) from among the points on level 1.† In contrast, in the version of the experiment conducted in class the consumer chose the point (9,3), where the consumerís willingness to pay for the marginal unit of good X was also 3 units of good Y.†
Note, though, that consumers had to be at least as well off in every round than they were in the version of the experiment conducted in class.† They could attain level 1 with a lower expenditure than previously, so given the same income they had to be at least as well off in every round.
Analogous to the version of the experiment conducted in class, if the consumerís income is increased then the consumer will increase his or her consumption of good X.† Therefore, the demand curve for good X at an income of $180 cannot lie to the left of the demand curve for good X at an income of $90.
Based on this discussion, the answers to the
individual questions, with points allotted to the questions, are:
[5]
9. True
[4]
10. Falseóin round 1 and also rounds 4 and 6 the consumer would choose the
point with 8 units of good X.
[5]
11. False
[4]
12. True
[7]
13. Falseóround 1 is a counterexample.
[4]
14. False
[4]
15. False
3. The average annual % growth in real GDP due to the
growth in labor is computed as the fraction of GDP paid to labor times the
average annual % growth in labor and the average annual % growth in real GDP
due to the growth in capital is computed as 1 minus the fraction of GDP paid to
labor times the average annual % growth in capital.† Let f denote the fraction of GDP paid to
labor, which is the same in
††††††††††† The average annual % growth in real GDP due to technical change is computed as a residual.† It equals the average annual % growth in real GDP minus both the annual average % growth in real GDP due to the growth in labor and the average annual % growth in real GDP due to the growth in capital.† Letting f represent the fraction of GDP paid to labor, then the average annual % growth in real GDP due to technical change can be computed as:
Average annual % growth in real GDP due to technical change = Average annual % growth in real GDP Ė f * Average annual % growth in labor Ė (1 Ėf) * Average annual % growth in capital.
Then the average annual % growth
in real GDP due to technical change in
†Average annual % growth in real GDP due to technical change in China = 10% - f * 9% - (1-f) * 15%
Average annual % growth in real
GDP due to technical change in
Subtracting the average annual % growth in real GDP due to technical change in India from the average annual % growth in real GDP due to technical change in China yields:
[10% - f * 9% - (1-f) * 15%] - [8% - f * 7% - (1-f) * 10%] = 2% - f * 2% - (1-f) * 5% < 2% - f * 2% - (1-f) * 2% = 0.
Therefore, the average annual % growth in real GDP due to
technical change must have been less in
% annual growth in real GDP due
to technical change in
This implies that the percentage annual growth in real GDP
in
Based on this discussion, the answers the individual
questions, with the points allotted to them in brackets, are:
[4]
16. True
[6]
17. True
[7]
18. True
[4] 19. False
[4] 20. False