| home |
| theory |
| apparatus |
| procedure |
| bibliography |
| contact |
Background on Muscovite Mica
Muscovite mica, a solid compound with formula KAl2(AlSi3O10)(OH)2, is a so-called 2:1 clay mineral because there are two layers of silicon atoms tetrahedrally coordinated by oxygen and one aluminum atom layer octahedrally coordinated by oxygen for every unit cell (called a micelle). The combination produces a structure with a net –1 charge that is neutralized by sheets of potassium ion, one sheet per micelle, located between adjacent micelles. The figures below,1 borrowed with permission from the website of Dr. Robert Harter, emeritus professor of soil chemistry at the University of New Hampshire (see websites at the end of this page), show a side view of the structure and a perspective view of the surface. The purple spheres are potassium ions, the greenish spheres are silicon, the brownish ones are aluminum, and the red ones are oxygen. The perspective view shows well that potassium ions reside on a plane and sit in hexagonal oxygen rings. As it happens, potassium has the perfect size to fit in these rings. The surface site area2 is 0.458 nm2.
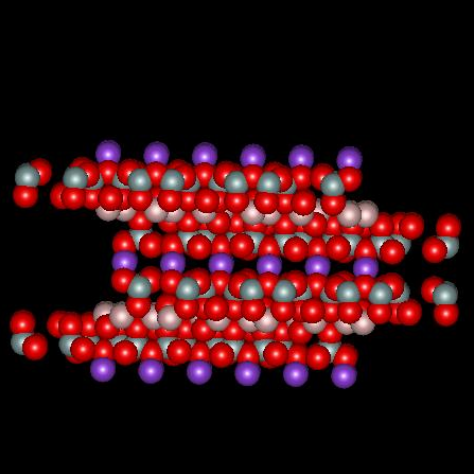
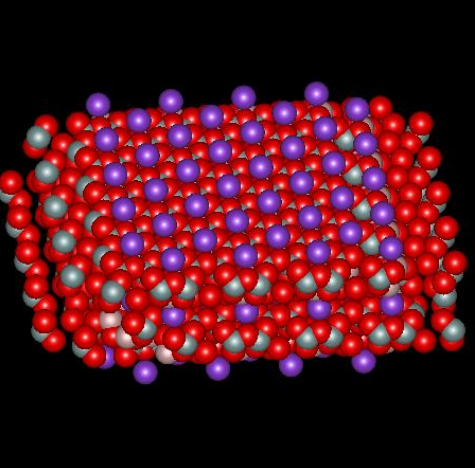
When mica is cleaved, i.e. when we use tape to pull off a sheet of it, the surface is effectively neutral. When it comes in contact with solution, potassium ions dissociate from the surface, which leaves unbalanced negative charge on the surface. It is interesting to calculate the charge density on the surface and inquire about what zeta potential corresponds to that surface charge, in a crude sense. If there is one negative charge per 0.458 nm2, the corresponding charge density is -0.35 coulombs per m2. Assume the surface is completely dissociated and there are no adsorbed ions. In this case the charge of the diffuse part of the double layer balances the charge on the surface. The Gouy-Chapman theory gives a relationship between the charge in the diffuse layer and the zeta potential of the surface, where zeta here is taken to be the potential at the Outer Helmholtz Plane.

Note the dependence of zeta on the charge density in the diffuse layer and on the Debye length. For a negatively charged surface, which attracts positive shielding charge, the zeta potential is negative. If the charge is held constant and the concentration of ions in the bulk solution is increased (causing a decrease in the Debye length), the zeta potential decreases in magnitude. Thus the magnitude of the zeta potential increases as the charge increases, and it decreases as the ionic strength increases at constant charge. Putting in values for the charge density as per above and the other parameters, one calculates a zeta potential of -270 mV. This value can be compared to values documented in the literature by Scales et al. [Scales90] For example, they measured the zeta potential of mica to be approximately -120 mV in 0.2 mM KCl, thus it seems that there is more to the question of what controls the charge on a mica surface than just the dissociation of potassium ions.
In fact the whole question of what establishes the charge on mineral surfaces is a complicated subject and ground, so to speak, much tilled by everyone from soil scientists to colloid chemists. One model for mica due to Scales et al. [Scales90] and appropriate for the pH range between 5 and 8 is sketched here. They proposed a single site dissociation model for the surface coupled to a three-layer model for the double layer. The three layer model for the double layer comprises a diffuse layer, an outer compact layer between the OHP and the IHP, and an inner compact layer between the solid surface itself and the IHP. Each of these three layers has a capacitance associated with it. The diffuse layer capacitance is given by the GC theory, the inner compact layer capacitance is assigned a high value, and the outer compact layer capacitance is used as a fitting parameter in their model.
The single site dissociation model comprises two equilibria: Let S- represent a singly charged surface site (probably a silicate structure) abandoned by potassium ion upon contact with water. In fact the surface density of free sites S- equals the surface density of charge. The following equilibria are in action in KCl solution:
SH <--> S- + H+ (1)
SK <--> S- + K+ (2)
Eq 1 represents the reversible interaction of protons with the surface sites, while eq 2 represents the reversible interaction of potassium ions with the surface sites. Protons and potassium ions neutralize the sites with which they are complexed. As one raises the pH, protons are subtracted from the surface. As one raises the KCl concentration, there are more potassium ions pushing the equilibrium of eq 2 toward complexing of the surface by potassium.
Equations 1 - 3 provide a foundation for interpreting zeta potential data on mica. The charge on the surface, and hence the zeta potential, clearly depend in a complex manner on the environment in which the mica finds itself. And even this is not the whole story. Outside the limits of 4 < pH < 8, other effects can occur. For example other investigators [Lyons81] have found that acid leached aluminum ions from mica and that mica stored in acid solution resembled adopted the electrokinetic characteristics of alumina when the pH was subsequently increased, reflecting deposition of aluminum oxide species on the surface.
- See http://pubpages.unh.edu/~harter/crystal.htm and http://pubpages.unh.edu/~harter/muscovite.html for more about the structure of muscovite mica.