Vibration #3: Vibration in a Saxophone Reed

 

Introduction: In this example you will execute modal analysis of a saxophone reed and find its natural frequencies.

Physical Problem: The reed is as defined below. The model is simpler than a true reed so the general idea is so determine the behavior of a closely similar physical model using the exact material model. The frequencies will be similar. It is firmly attached along the back 3cm of its length.

Problem Description:

 

·         The reed has dimensions as explained in the diagram.

·         The reed is made of bamboo with a Young's modulus of 28.8e6, Poisson's ration of 0.3, and a density of 1158 kg/m².

·         Assume the reed is connected to the mouthpiece and is fixed in all degrees of freedom. The reed is solid and has material properties that are constant and isotropic.

·         Objective:

            To determine the natural frequencies of vibration

            To generate animations of these vibrations.

Figure:

 

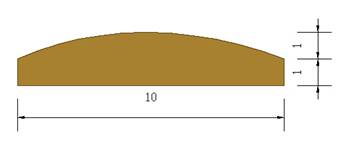 (mm)

 

 

 

IMPORTANT: Convert all dimensions and forces into SI units.

 

·         Create the cross-sectional area of the reed using key points to define the 4 edges of the rectangular solid portion, and one key point in the middle of the arc in the top of the reed to map a spline.

·         Set the Material Properties of the reed. (Hint: Elastic Modulus, Poison’s Ratio, and Density are important to define

·         Define two types of elements: Quad 4node 42 and Brick 8node 45.

·         Use the mesh tool to set the Global Mesh size to 0.00025 and mesh the cross-section using the 2D mesh set from element type 1.

·         Extrude the shape using the second element type (Brick 8node) 8cm in the Z direction. (Don’t mind the warning. If we were using a full version of ANSYS, we would be able to choose SOLID95 instead, which would extrude without error.)

·         Set the Boundary Conditions.  (First unselect the Plane 42 elements used in the 2d area mesh.  Next, apply the DOF constraints to the end of the reed such that 0.03m of the reed is unable to move.  Finally, reselect all nodes.)

·         Solve for the natural frequencies of vibration of the vocal chords. (Use a modal analysis using the Block Lanczos Mode Extraction method and solve for 5 modes.)

·         List the nodal frequencies of vibration for the vocal chords.

·         From the results obtained, read the first set, then animate the mode shape using 30 frames with a 0.25 second time delay between frames.  Be sure to show the DOF Solution with both the Deformed and Undeformed Edge.  This will properly demonstrate the vibration patterns in the vocal chords.

·         Plot the nodal solutions to use as screenshots and compare with the answers below.  

 (These are the results you should expect:)

 

 

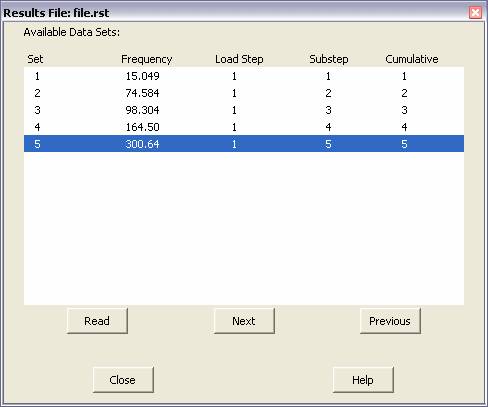
 (Modes of vibration:)

First

RIGHT

 

Second

TOP

 

Third

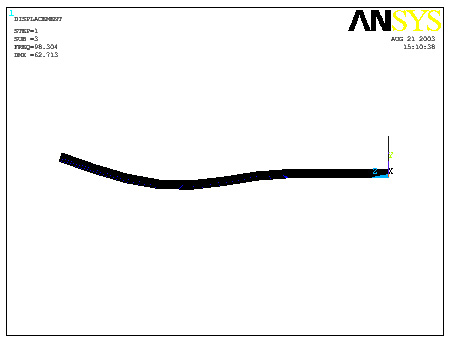RIGHT

 

Fourth
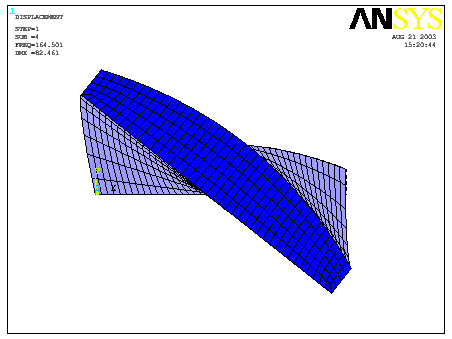FRONT

 

Fifth

ISO