Overview

The objective of this laboratory is for you to become familiar with accelerometers and impact hammers, which are commonly used to measure vibration response of a structure. In this lab, you will make several simple measurements of transient vibration that will illustrate the concepts of natural frequency, damping ratio and elastic wave speed in solids. You will also learn how to measure a frequency response function and identify the resonant frequency.

Damped vibration is described in terms of the natural frequency w_n and the damping ratio z . A typical free response can be modeled by the expression

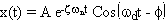
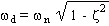
where A and f are the peak amplitude and phase angle, as determined by the initial conditions. We can note that if we sample the response at the peak times t_k of each oscillation cycle, then the amplitude of those points simply decays exponentially. Since the cosine function will be one at those points, we have

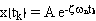
Thus, the envelope of the vibration decays in a manner that looks exactly like a first-order system. We know that the time between successive oscillation cycles is given by

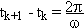
We can therefore write

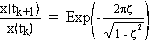
which provides the fractional amount of amplitude reduction that we see after one cycle of motion has elapsed. After N cycles,

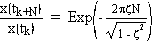
Thus, by measuring the reduction in amplitude over some number of cycles, we can determine the value of the damping ratio. In practice, we make measurements for several values of N, and average the results. Note that in the above equations, z is usually small when compared with unity for underdamped motions.

2. Elastic Wave Speed

The speed for the propagation of tension/compression waves is given by

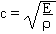
where E is the material’s elastic modulus, and r is the density.

Frequency response function is the response amplitude of the system as a function of forcing frequency. It turns out that, in the sense of a Fourier series, an impulse (or hammer hit) has components at many different frequencies. Thus, striking a structure with a hammer is analogous to exciting it with sinusoidal excitation at many frequencies all at once. The spectrum of such a response is called the frequency response function.

Assignment:

1. Plot the free-vibration response of a structure using the equation given in these instructions (the very first equation). Assume that the structure's natural frequency is 120 Hz. Assume three cases of damping; undamped (z=0), slightly damped (z=0.03), and highly damped (z=0.10). Plot all cases for a period of 50ms with at least 10^-5 time steps. For ease of calculation, you can set A=1, f=0). After plotting, compare there cases of damping and comment on the effect of damping on vibration response.

2. Using the equation given for elastic wave speed in solids, calculate the wave speeds in steel, cast iron, aluminum, concrete and wood. Compare the wave speed in these solids, in which medium the waves propagate fastest and slowest? You can pick up the properties of these materials from any Strength / Mechanics of Materials textbook.

The accelerometers and impact hammers at each laboratory station contain built-in micro-electronic amplifiers, and piezoelectric crystals. These are rigid quartz crystals that, when subjected to strain, produce an electric charge. This charge can be measured to indicate the force that is acting on the crystal (as in the impulse hammer), or the acceleration to which the transducer is subjected (as in the accelerometer). These transducers are small, fragile, and expensive. In particular, it is relatively easy to damage the wires, and so be sure to use with caution when handling them. In addition, power supply units are battery powered, please turn them off when you finish your measurements.

• By using C-clamps, fix the test instrument to the table. It should be fixed tightly and preferably at midpoint.

   

• Connect Impact Hammer
  • Connect the impact hammer to the input jack of a power supply unit using a BNC cable.
  • Connect the output jack of the power supply unit to Channel 1 of oscilloscope using BNC cable.

   

• Connect Accelerometer
  • Connect the accelerometer to the input jack of a second power unit using a microdot-BNC cable. These cables are white, with different shaped connectors on the ends.
  • Connect the output jack of the power unit to Channel 2 of the oscilloscope using a BNC cable.
  • Place the accelerometer to the end-mass. If necessary, use some of the red adhesive wax that is supplied in each accelerometer kit to stick the accelerometer to the structure.

   

• Turn on the both power units and oscilloscope.

   

1. Natural Frequency and Damping Ratio Measurement

• Currently impact hammer signal is sent to Channel 1 and accelerometer signal to Channel 2 of the oscilloscope. Display Channel 1 on upper half and Channel 2 on lower half of the oscilloscope screen.
• Set Time/Div to 20ms and Horizontal Delay to 80 ms.
• Set Volts/Div to 1V on both channels.
• Set Trigger Source to Channel 2 and Trigger Mode to Single. Trigger Level should be around 0.0 Volts.
• Press Run button on the scope and hit the impact hammer to the structure at a point between the cantilever-end and mid-mass. Since the scope is in Single Trigger mode, you need to press Run button each time to repeat the measurement.
• A free response time history of acceleration will look like an exponentially decaying Sine wave. Using the cursors, measure and record the Dt between two consecutive maxima or minima. Repeat this measurement for other consecutive peaks to confirm it. This value is the period of oscillations and its inverse is fundamental frequency.
• To estimate the damping ratio, using scope's cursors, measure the voltage values of several maxima or minima together with the number of cycles between those points. (Remember: Set Cursor Source as Channel 2 and set V1 cursor at zero level of this channel, then measure peak values using V2 cursor and record DV).
• Print this screen to include your report.

2. Elastic Wave Speed Measurement

• Set Horizontal delay to zero and then set Time/Div to 100 ms.
• Place the accelerometer at one end of the aluminum I-beam, and strike the other end with the hammer so that longitudinal tension and compression waves are excited. When you hit the test fixture, the scope triggers and simultaneously displays the transient waveforms for the hammer and the accelerometer.
• You will see a definite lag between the times when you first hit the beam, and when the accelerometer began to record motion at the beam's other end. Measure this time delay. Repeat the experiment several times and average values obtained from these measurements.
• From the measured time delay, and the length of the beam (0.377m), you can determine the elastic wave speed.
• Print a representative set of waveforms from the scope and include them in your lab report.

3. Frequency Response Function Measurement

• Attach the accelerometer to the end-mass again as in the first part.
• Detach the BNC cables from oscilloscope's Channels 1 and 2 and connect respectively to Channel 1 and 2 of Spectrum analyzer.
• Turn off the scope and turn of the spectrum analyzer.
• Configure the analyzer's display;
  • On the SYSTEM keypad, press the green button labeled PRESET. Then press F1 for DO PRESET to set the analyzer to the default configurations.
  • On the MEASUREMENT keypad, press INST MODE and select F9 to set the instrument to 2 Channel mode.
  • On the DISPLAY keypad, press DISP FORMAT, and then F2 to select Upper/Lower windows.
  • On the DISPLAY keypad, press MEAS DATA, and then F7 on the softkeys to select FREQUENCY RESPONSE.
  • On the DISPLAY keypad, press ACTIVE TRACE and then F7 on the softkey to select FREQUENCY RESPONSE. This will set both windows A and B to display frequency response information.
  • On the DISPLAY keypad, press TRACE COORD and then F4 to select PHASE. The upper window should now show the magnitude of the Frequency Response Function in dB, and the lower window should show the phase angle in degrees.
  • On the DISPLAY keypad, press SCALE, and then F1 to set AUTOSCALE ON for lower window. Now press ACTIVE TRACE on the DISPLAY keypad to toggle from lower window to upper window, then press F1 again to set AUTOSCALE ON upper window.

   

• Setting up the measurement parameters;
  • On the MEASUREMENT keypad, press AVG and then F1 to set the analyzer to AVERAGE ON. In this manner, results from several successive impacts of the hammer will automatically be averaged. The default number of averages is 10. Change this number to 25 by pressing F2 for NUMBER AVERAGES and enter 25 using the numeric keypad, then press F1 to ENTER.
  • On the MEASUREMENT keypad, press FREQ and then F1 to set the frequency SPAN. Using numeric keypad enter 800 and press F2 to set Hz. The upper lines of the display should indicate a start frequency of 0 Hz, a stop frequency of 800 Hz and a resolution of 400 lines. Of course, you will get odd looking results if the analyzer happens to be set for 102.4 kHz and you are measuring the motion of something with a frequency of only 50 Hz.
  • On the MEASUREMENT keypad, press WINDOW and then F1 to select the HANNING window for computation of the Fourier Transforms.

   

• Acquiring data;
  • Press the yellow START key on the MEASUREMENT keypad. After a slight delay, the analyzer will begin computing averaged frequency response functions, and displaying the current average on the screen. Hit the structure lightly but firmly with the hammer approximately once every several seconds. When all the averages have passed (the average count is displayed on the screen), the final result is displayed and the test is complete.
  • Before acquiring valid data for your experiment, you will need to make several preliminary runs as in the above paragraph, during which time the analyzer will automatically calibrate itself and select the proper voltage range for your input signal. When you do not see a highlighted overload indicator for Channel 1 (OV1) or for Channel 2 (OV2), then the analyzer’s result is acceptable.
  • Generate hardcopy plots of the measured FRF amplitude and phase. Before printing, press LOCAL/HP-IB button on SYSTEM menu. Then press F2 to select SYSTEM CONTROLLER. To print, press PLOT/PRINT button on SYSTEM menu, then press F10 for MORE SETUP and F2 to select DEVICE IS PRNT, then F10 for RETURN. Finally press F1 to START PLOT/PRNT.
  • The amplitude of Frequency Response Function (FRF) is in dB in this plot, we also want to prepare a plot in Linear Magnitude. On DISPLAY keypad, press TRACE COORD button, then F1 to select LINEAR MAGNITUDE, you may need to AutoScale it again, press SCALE on DISPLAY keypad, then F1 for AUTOSCALE. Now read and record the two dominant peak frequencies.
  • Print this screen too to include in your report. Simply, press PLOT/PRINT button on SYSTEM menu, and then press F1 to START PLOT/PRNT.

   

  ---

  Part III: Laboratory Report

  Address all of the points raised above, and include in your report the oscilloscope and analyzer plots for the tests.

  1. What is the period, fundamental frequency and damping ratio of the system. Include a data table to show the amplitudes of vibration that you used in finding the damping ratio.

  2. Why is there a delay between impact hammer and accelerometer readings? What are your measured values for Dt and average Dt? What is the corresponding wave speed in the I-beam? Also compare the measured wave speed value with the one expected by theory? (use the formula given in the handout and keep in mind I-beam is made of aluminum.) If you have used a solid circular cross-section beam instead of I-beam but made of same material, would you expect any change in wave speed? Why or why not?

  3.Discuss how the analyzer is useful in determining natural frequencies of structures. Why an engineer is interested in obtaining natural frequencies of the system?

  4. What is the frequency value of the first dominant peak in the frequency response function (use linear magnitude plot)? What is the meaning of it? Compare this value with the fundamental frequency.

  5. Why are there multiple peaks in the frequency response function? Does acceleration response of the cantilever beam appear to be a pure exponential decaying Sine wave or not? Why or why not?