Reading

• Chow and Johnson: N/A
• Coulouris, et al: N/A

Looking Ahead

Today, we are going to begin coverage of a traditional operating system issue, but this time in a distributed environment: process allocation and migration. We are going to ask the question, "Given many different processors, which one do we use and when is appropriate to move to a different one?"

But, before entering into that discussion, I would like to discuss some preliminary concepts relavent to distributed scheduling. So, we'll begin by looking at the economies of multiple processors, and then examine threas, processes, and tasks in a distributed setting.

You Choose: One or N

Which is preferable, 1 processor, or N processors, each of which is 1/N^th as powerful?

In response to this question, most people point out the following characteristics:

• Both options are equally "powerful"
• 1 processor is more likely to be completely functional than N processors, each of which has the same likelihood of failing as the single processor. If it is "all or nothing", this might suggest that the single processor is more robust.
• The N processors are less likely to completely fail than the single processor. In other words, if progress can be made with only some of the processors, the N processors are "fail soft".

The surprising finding is this: The response time is better for a system with one processor than N processors which are 1/N^th as powerful. How can this be possible? Simple math shows: N*(1/N) = 1.

Let's see if we can think our way through this situation. Let's begin by defining response time to be the elapsed time between the arrival of a job and the time that the last piece of the result is produced by the processor(s). Now let's assume that there is only one job in the system and that this job is indivisible and cannot be parallelized. It is fair to assume that the job cannot be divided and conquered, because any job can be reduced to a piece that is atomic. This indivisible piece is what we will now consider.

Let's say that this job takes one unit of time in our one processor system. If this is the case, it will take N units of time if executed in the N processor system. The reason for this is that the job can only make use of one processor, so it can only utilize 1/N^th of the power of the N procesor system.

Now if we assume that we have an endless stream of jobs, it might seem like this problem goes away -- we can make use of all of the processors concurrently. And, although this is true, it doesn't quite work out so well in practice. As each job arrives, it must be placed on the queue associated with one of the processors. Some queues may become long and other queues may be empty. The backlog that builds up on the queues that happen to be long is a penalty, whereas the unused cycles on the available processors offer no reward.

If the arrival rate is less than the service time (which makes sense, if we hope ever to complete all of the work), we can model the mean response time for a system with a single processor and a single queue as below:

If you want to try to understand the formula above, you can think of it this way. Take a look at the denominator of the equation. It subtracts the arrival rate from the service rate. In other words, it asks the question, "In each unit of time, if we execute all of the jobs we have, how many jobs worth of time is left unused?" If we have another job to submit, we must fit it into this unused time. The question then becomes, "How many units of time does it take for me to acquire enough left-over time to execute the new job?" This subtraction yields the number of fractional jobs that are left over per unit time, in this case seconds. By inverting this, we end up with the number of units of time measured that are required to execute the new job -- this includes the busy cycles that we spend waiting, and those cycles used ofr the new job.

It might make sense to view this as a periodic system, where each "unit of time" is a single period. The mean response time is the mean case for many periods it wil take for use to find enough spare cycles to complete our job. The piece of each period that already used represents the cycles spent on th jobs ahead of us on the queue.

Given this, we can model the average queue length as below:

In other words, if the system is at 80% capacity, L = (0.8/(1-0.8)) = (0.8/0.2) = 4

Again, a quick look at this can give us some intuition about why it is true. If there are no spare cycles, the load average will be one and the denominator will be 0, yielding an infinite expected queue length. If the load average is 0, there are no jobs in the system, so the queue is empty. If the load average is 80% or 0.8, we can only use 20% or 0.2 of each period for our job. This means that if our job requires 80% of a period, we will have to wait 4 periods to acquire enough cycles, hence an expected queue length of 4.

Given this, what happens if, instead of have one processor that has the power of all N processors? Since it can handle N times as many jobs in the same time, the service rate is N times greater. Since it is handling the jobs that were previously spread out over N queues on the same queue, the arrival rate is N times greater. following:

Notice the surprising result: We get an N times speedup by having one processor, instead of N processors that are each 1/N^th as powerful!

If we service a pool of processors using a single queue, we find our performance is somewhere in the middle. The service time is much like having a single very powerful processor, with a single queue, except the job take longer once it is dispatched, because the processor that is executing it remains slower. For reference, the figure below shows all three configurations:

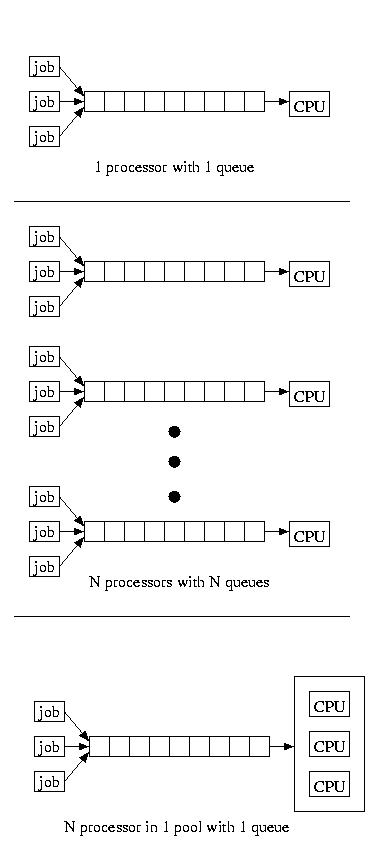
It is a good thing for us that it is cheaper to by N slower processors than a processor N times as fast -- otherwise distributed and parallel systems would become less interesting (at least for the purpose of improving the response time for computationally intensive tasks).

So, although distributed systems might not be useful for reducing the response times for large, indivisible tasks, they can yield more processing power for less money, greater availabilty, and greater accessibility for distributed user communities.

Threads, Processes, and Tasks

When teaching operating systems, I introduce processes, tasks, and threads, much as I will today. For those of you who come to us from 15-213, this discussion will not be entirely unfamiliar -- we painted the same picture with a larger brush in 15-213.

In earlier times, computers were used to automate highly structured processes. It wasn't the case that the word process was arbitrarily selected as the name of the structure, within an operating system, that represents a unit of user work. It was the case that users had processes, in the conversational sense, that they wanted computers to follow. These processes were processes whether represented in high-level code or assembly code, or more human forms such as flow charts for business processes or systems of equations for mathematical processes.

Over time, the problems that people wanted to address by computer became more complex. They could no longer easily be described using a single flow of control. Instead, they were constructed by implementing multiple concurrent, but interacting processes. Unfortunately though, the old process structure implemented by operating systems was not well-suited to this model.

Operating systems were designed to keep processes separate and invisible to each other. Philosophically, this was, and remains, one of the goals of operating systems: Allowing multiple processes to share the same system, without knowing that they are sharing. And, perhaps more importantly, keeping processes seaprate and hidden from each other ensures that one process can not accidentally or maliciously damage another. Unfortunately, climbing over the protective walls to allow processes to communicate is, for reasons that we discussed in operating systems, not cheap.

Eventually, a new abstraction was born, the thread, and abstraction for a thread of control or one process within a task that might contain one or more separate processes. Much like "process" means much the smae thing in a human context as it does in the domain of operating systems, the meaning of "task" is clear to even the uninitiated observer. A task is nothing more than a unit of user work -- whether it is a single process or multiple processes.

Modern operating systems implement protection around tasks, but allow the threads within a task to share the same resources and enjoy the reduced cost of interaction -- even if it means a greater risk of damage to one thread by another.

For the curious, threads were originally born as an abstraction for concurrency within the operating system kernel, and then mimiced at the user level using libraries. Only relatively recently have operating systems implemented the task abstraction and provided kernel-level support for user-level tasks composed of multiple threads of control.

Threads, Processes, Tasks -- And Distributed Systems

I'm going to tell a slightly different story in the context of this class, Distributed Systems. For our purposes, let's not worry about precisely defining threads and processes. Instead, let's instead discuss tasks.

Today, I am going to tell you that a task is the environment in which a thread executes. What do I mean by this? A task is the collection of resources required to perform work on behalf of a user. It consists of everything that is actually required by the logic, all of the resources. For example, a task is composed of open files, open network sockets, memory objects, and registers.

A thread is the logic behind the user's work and is influenced by and manipulates the resources within the task. So, a task might contain a single thread of control, or many threads of control. We'll call tasks composed of a single thread of control processes.

Processor Allocation and Process Migration in Distributed Systems

Our discssion is going to involve picking a processor to run a process and moving that process from one processor to another when appropriate. Processor allocation involves deciding which processor should be assigned to a newly created process, and as a consequence, which system should initially host the process.

In our discussion of process migration, we will discuss the costs of associated with moving a process, how to decide that a process should be migrated, how to select a new host for a process, and how to make the resources originally located at one host available at another host.

Although these algorithms will be discussed in the context of processes, task with only one thread, they apply almost unaltered to tasks containing multiple threads. The reason for this is that the interaction of the multiple threads with each other and the environment almost certainly implies that the entire task, including all of its threads, should be migrated whole -- just like a single-thread process. Unlike multiprocessor computers, it only very rarely makes sense to dispatch different threads to different processors, or to migrate some threads but not others. In distributed systems, the cost of sharing resources on different hosts is usually far too high to allow for this level of independence.