Return to the lecture notes index
March 17, 2008 (Lecture 21)
Reading:
- Coulouris, et al: 13.6
- Chow and Johnson: 13.1 - 13.5
Credit
Much of today's discussion follows chapter 13 of the Chow and Johnson
textbook. Additionally, the figures used in class today were based on those
in this book. The bibliographic information, which also appears in the
syllabus, is as follows:
Chow, R. and Johnson, T., Distributed Operating Systems & Algorithms,
corrected 1st edition, AWL, 1998, ISBN: 0-201-49838-3.
Recovery from Failure
As you know, distributed systems are very likely to suffer from failure.
This is a characteristic of their scale. Sometimes we have sufficient
redundancy to keep failures transparent. On other occasions, we need to
repair or replace failed processors and pick up we we left off before the
failure. This process is known as recovery.
When I was a sophomore taking a data structures class, a PhD student was
performing research involving parallel tree algorithms using a tool
known as the Parallel Virtual Machine (PVM). PVM allowed one to write
software to use networked computers to emulate a multiprocessor system.
But networks are notoriously less reliable than the bus of a single
multiprocessor system. And workstations, especially those in publically
accessible labs, are also far less reliable than the processors in a
single multiprocessor system.
This is especially the case when the PVM processes are running with
a very high priority during the time when an undergraduate lab is
being held in the publically accessible lab. And even more so, when
the very high priority is sufficient to render the workstations unusable
by the students in lab.
In this case-in-point, a student (or students) frequently power-cycled his
(err, or her, or their) workstation in order to kill the PVM job and finish
his (err, or her, or their) lab work. Afterall, the PhD student would
certainly be smart enough to periodically save partial results in the
event of such a failure, right? Whmmm....well maybe not, rumor has it
someone was a student a semester longer than expected...)
Needless to say, recovery is a very important component of many real-world
systems. Recovery ususally involves checkpointing and/or
logging. Checkpointing involvs periodically saving the state of
the process. Logigng involves recording the operations that produced the
current state, so that they can be repeated, if necessary.
Let's assume that one system fails and is restored to a previous state
(this is called a rollback. From this point, it will charge
forward and repeat those things that it had done between this previous
state and the time of the failure. This includes messages that it may
have sent to other systems. These repeated messages are known as
duplicate messages. It is also the case that after a rollback
other systems may have received messages that the revovering system
doesn't "remember" sending. These messages are knwon as orphan
messages.
The other systems must be able to tolerate the duplicate messages, such
as might be the case for idempotent operations, or detect them
and discard them. If they are unable to do this, the other systems
must also rollback to a prior state. The rollback of more systems
might compound the problem, since the rollback may orhpan more messages
and the progress might cause more duplicates. When the rollback
of one system causes another system to rollback, this is known as
cascading rollbacks. Eventually the systems will reach a state where
they can move forward together. This state is known as a
recovery line. After a failure, cooperating systems must rollback
to a recovery line.
Another problem involves the interaction of the system with the real-world.
After a rollback, a system may duplicate output, or request the same
input again. This is called studdering.
Incarnation Numbers
One very, very common technique involves the use of incarnation
numbers. Each contiguous period of uptime on a particular system
is known as an incarnation of that system. Rebooting a system
or restarting a cooperating process results in a new incarnation.
These incarnations can be numbered. This number, the incarnation number,
can be used to eliminate duplicate messages. It must be kept in
stable storage, and incremented for each incarnation.
When a system is reincarnated, it sends a message to the cooperating
systems informing them of the new incarnation number. The incarnation
number is also sent out with all messages.
The reciever of a message can use the incarnation number as follows:
- If the incarnation number in the message is less than the
expected incarnation number, the message is a duplicate,
so it should be discarded.
- If the incarnation number in the message is greater than the
expected incarnation number, the sender is recovering, so
block accepting messages, until it informs us about its new
incarnation number.
- If the incarnation number is the same as the expected incarnation
number, accept the message.
Uncoordinated Checkpointing
One approach to checkpointing is to have each system periodically
record its state. Even if all processors make checkpoints at the
same frequency, there is no guarantee that the most recent checkpoints
across all systems will be consistent. Among other things, clock
drift implies that the checkpoints won't necessarily be made at
exactly the same time. If checkpointing is a low-priority background
task, it might also be the case that the checkpoints across the systems
won't necessarily be consistent, because the systems may have cycles
to burn at different times or with a completely different frequency.
In the event of a failure, recovery requires finding the recovery lines
that restores the system as a whole to the most recent state. This is
known as the maximum recovery line.
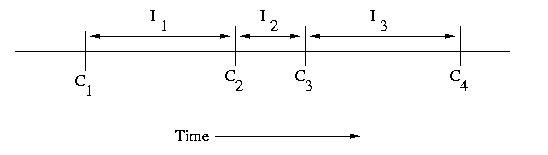
An interval is the period of time between checkpoints. If
we number checkpoints, C1, C2, C3,
C4, &c., the intervals following each fo these checkpoints
can be labeled I1, I2, I3,
and I4, respectively. it is important to note
that the intervals need not be the same length.
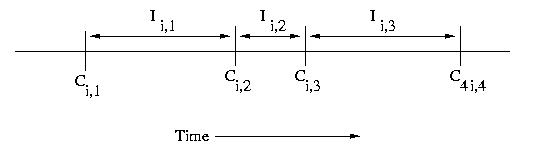
If we have multiple processors, we can use subscripts such
as Ci,c and Ii,c, where i is the processor number
and c is the checkpoint sequence number.
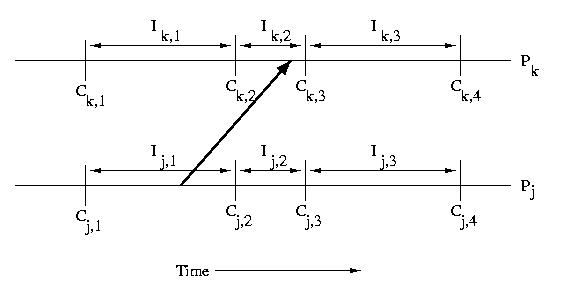
When a processor recieves a message, that message usually causes it
to take some action. This implies that the processor that receives
a message is dependent on the processor that sent the message.
Specifically if a processor receives a message during an interval,
it is dependent on the interval on the sender's processor during
which the message was sent. This type of dependency can cause
cascading rollbacks.
In the example below, Ik,2 depends on Ij,1
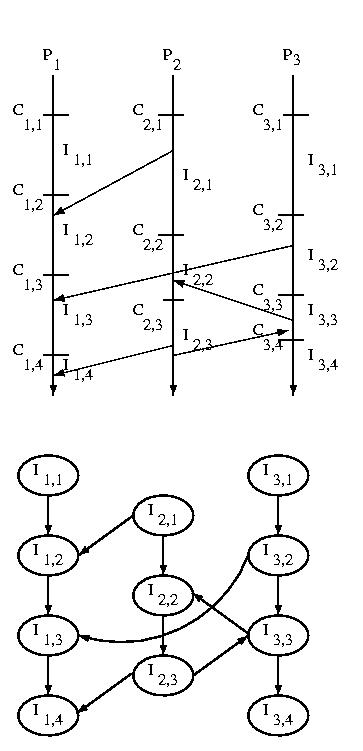
If we consider the messages sent among systems we can construct
an Interval Dependency Graph (IDG). If any intervals are
removed from the graph due to rollbacks or failures, we must
remove all intervals that they reference -- this is a transitive
operation.
The graph is constructed by creating a node for each interval,
and then connecting subsequent intervals on the same processor by
constructing an edge from a predecessor to its successor. Then
an edge is draw from each interval during which one or more messages
were received to the inteval or intervals during which the message(s)
was or were sent.
The edge form one interval to its success on the same processor
exists to ensure that we can't develop "holes" in our state
-- a hole would imply wasted checkpoints -- those before the
hole would be useless.
The edge from a receiver to the sender shows the dependency of
the sender on the receiver. Remember that the arrow goes the
opposite way in the IDG than it did when we showed the message
being sent earlier -- this is because the sender is dependent
on the receiver, not the other way around. If other actions
generate dependencies, they can be represented the same way.
Where is this graph stored? Each processor keeps the nodes and edges
that are associated with it.
How Do We Find The Recovery Line?
Very simply. Upon recovery, we tell other processors
what checkpoint we'll be installing. Then they rollback
to an interval independent of the lost intervals and
broadcast a similar message. This continues until
the recovery line is established.
Coordinated Checkpoints
We can decrease the number of rollbacks necessary to find a recovery
line by coordinating checkpoints. We'll discuss two methods for
doing this.
Recording Message Sequence Numbers
If messages contain sequence numbers, we cna use them to keep
track of who has sent us messages since our last checkpoint.
Each time we make a checkpoint, we send a message to each
processor that has sent us messages since the last time we
checkpointed -- we depend on these processors.
When these processors receive our message, they check to see if
they have checkpointed since the last time they sent us a message.
If not, they create a checkpoint, to satisfy our dependency in the
event of a failure.
Synchronized Clocks
Another method for coordinating checkpoints is to take advantage
of synchronized clocks, if available. Each processor creates a
checkpoint every T units of time. Since even synchronized clocks
may have a skew, we assign a sequence number to each checkpoint.
This sequence number is sent in all messages. If a processor
discovers that the sender has checkpointed more recently, it
creates a checkpoint. This checkpoint should be made before passing
the message up to the application -- this ensures that we remember
the message in the event of a failure, so the sender won't need to
rollback and resend.



