This approach makes some somewhat fairytale-like assumptions:
- All messages are delivered within some Tm units of time,
called the message propogation time.
- Once a message is received, the reply will be dispatched within
some Tp units of time, called the message handling
time.
- Tp and Tm are known.
These are nice, because together they imply that if a response is
is not received within (2*TM + Tp) units of time
the process or connection has failed. But, of course, in the real
world congestion, load, and the indeterminate nature of most networks
make this a bit of a reach.
The idea behind the Bully Algorithm is to elect the highest-numbered
processor as the coordinator. If any host thinks that the coordinator
has failed, it tries to elect itself by sending a message to the
higher-numbered processors. If any of them answer it loses the election.
At this point Each of these processors will call an election and try to
win themselves.
If none of the higher-ups answer, the processor is the highest numbered
processor, so it should be the coordinator. So it sends the lower level
processors a message declaring itself the boss. After they answer (or
the ACK of a reliable protocol), it sends them the new state of the
coordinated task. Now everyone agrees about the coordinator and the
state of the task.
If a new processor arrives, or recovers from a failure, it gets the state
from the current coordinator and then calls an election.

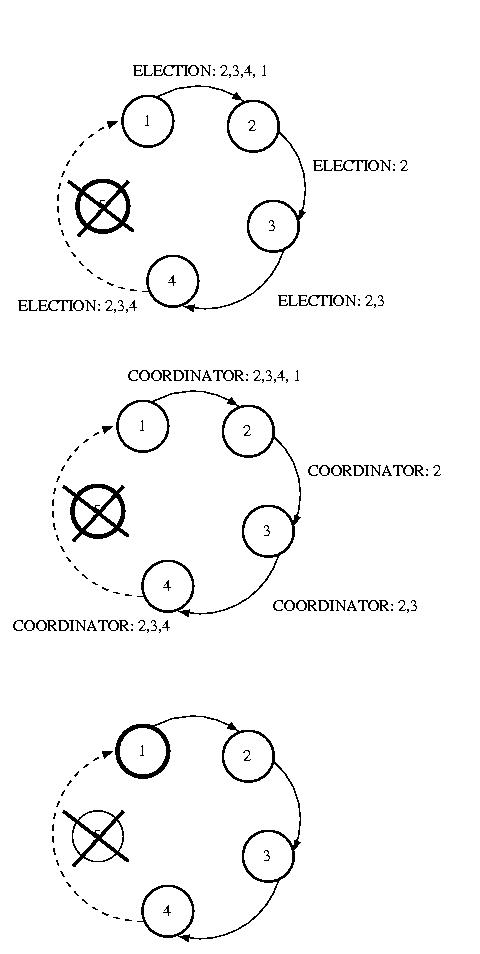
Another approach, Ring election, is very similar to token ring
synchronization, except no token is used. We assume that each processor
is logically ordered, perhaps by IP address, so that each processor
knows its successor, and its successor's successor, and so on. Each
processor must know the entire logical structure.
When a processor discovers that the coordinator has died, it starts
circulating an ELECTION message around the ring. Each node advances
it in logical order, skipping failed nodes as necessary. Each node
adds thier node number to the list. Once this message has made its
way all the way around the ring, the message which started it will
see its own number in the list. It then considers the node with the
highest number to be the coordinator, and this messages is circulated.
Each receiving node does the same thing. Once this message has made
its way around the ring, it is removed.
If multiple nodes concurrently discover a failed coordinator, each
will start an ELECTION. This isn't a problem, because each election
will select the same coordinator. The extra messages are wasted overhead,
while this isn't optimal, it isn't deadly, either.
The bully algorithm is simply, but this is because it operates under the
simplistic assumption that failures can be accurately detect failures.
It also assumes that failures are processor failures -- not network
partitions. In the event of a partitioning, or even a slow network and/or
processor, more than one coordinator can be elected. Of course, the timeout
can be be set large enough to avoid electing multiple processors due to
delay -- but an infinitely large timeout would be required to reduce this
proability to zero. Longer timeouts imply wasted time in the event of
failure.
Let's assume that in practice communication failure, high latency,
and/or congestion can partition a network. Let's also assume that
a collection of processors, under the direction of a coordinator, can
perform useful work, even if other such groups exist.
Now what we have is an arrangement such that each group of processors
that can communicate among themselves is directed by a coordinator, but
different groups of processors, each operating under the direction of
a different coordinator, can co-exist.
The Invitation Algorithm provides a protocol for forming groups
of available processors within partitions, and then creating larger
groups as failed processors are returned to service or network partitions
are rectified.
The Invitation Algorithm organizes processors into groups. Ideally all
processors would be a member of the same group. But network partitions,
and high latencies yielding apparent partitions, may make this impossible
or impractical, so multiple groups may exist. Each functioning processor
is a member of exactly one group.
A new group may be formed to perform a new task, because the coordinator
of an existing group has become unavailable, or because a previously
unreachable group has been discovered. Groups are named using a group
number. The group number is unique among all groups, is changed
every time a new group is formed, and is never reused. To accomplish this,
the group number might be a simple sequence number attached to the processor
ID. The sequence number component can be incremented each time the
processor becomes the coordinator of a new group.
Since the goal is to have all functioning processors working together in
the same group, the groups that resulted from network partitioning
should be merged once the partition is repaired. This merging is
orchestrated by the coordinators. The goal of every coordinator is to
discover other coordinators, if they are accessible. To achieve this
coordinators "yell out" perodically to each processor asking each if it
is a coordinator. Most processors, the participants, reply indicating
that they are not a coordinator. It is possible that some coordinators
are unreachable or don't reply before some timeout period -- that's okay,
they are perceived to be non-existent or operating in a separate partition.
Once one coordinator has identified other reachable coordinators, the goal
is for the coordinators to merge their groups of processors into one
group coordinated by one coordinator. Usually, it is acceptable to say
that the coordinator that initiated the merge will be the coordinator of
the new group. But it might be the case that two or more coordinators were
concurrently looking for other coordinators and that their messages may
arrive in different orders. To handle this situation, there should be some
priority among the coordinators -- some method to determine which of
the perhaps many coordinators should take over.
One way of doing this might be to use the processor ID to act as a priority.
Perhaps higher-numbered processors ignore queries from lower-level
processors. This would allow lower-level processors to merge the groups
with lower priority coordinators during this operation. At some later time
the higher-level coordinators will each act to discover other coordinators
and merge these lower-priority groups. Perhaps receiving the query will
prompt the higher-level coordinator to try to merge its group with others
sooner than it otherwise might. An alternative would be for a coordinator
only to try to merge lower-level coordinators.
Or perhaps processors delay some amount of time between the time that they
look for other coordinators and the time that they start to merge these
groups. This would allow time for a higher-priority coordinator to
search for other coordinators (it knows that there is at least one) and
ask them to merge into its group. If after such a delay, the old coordinator
finds itself in a new group, it stops and accepts its new role as a
participant. In this case, it might be useful to make the delay inversely
proportional to one's priority. For example, there is no reason for the
highest-priority processor to delay. But the lowest priority processor might
want to delay for a long time.
In either case, once the merging of groups begins, processing the
the affected groups should be halted -- the state may be inconsistent.
The coordinator that started the merge operation will become the
coordinator of the new group. It should increment the sequence number of
the group ID and tell the participants in its old group. It should also
tell the coordinators that it discovered to merge their partiticpants, and
themselves, into the new group.
Once this is done, the new coordinator should coordinate the state of the
partipants, and processing can be re-enabled.
If a node discovers that its coodinator has failed, is newly installed,
or returns to service after a failure, it forms a new group containing only
itself and becomes the coordinator of this group. It then searches for other
groups and tries to merge with them as described above.
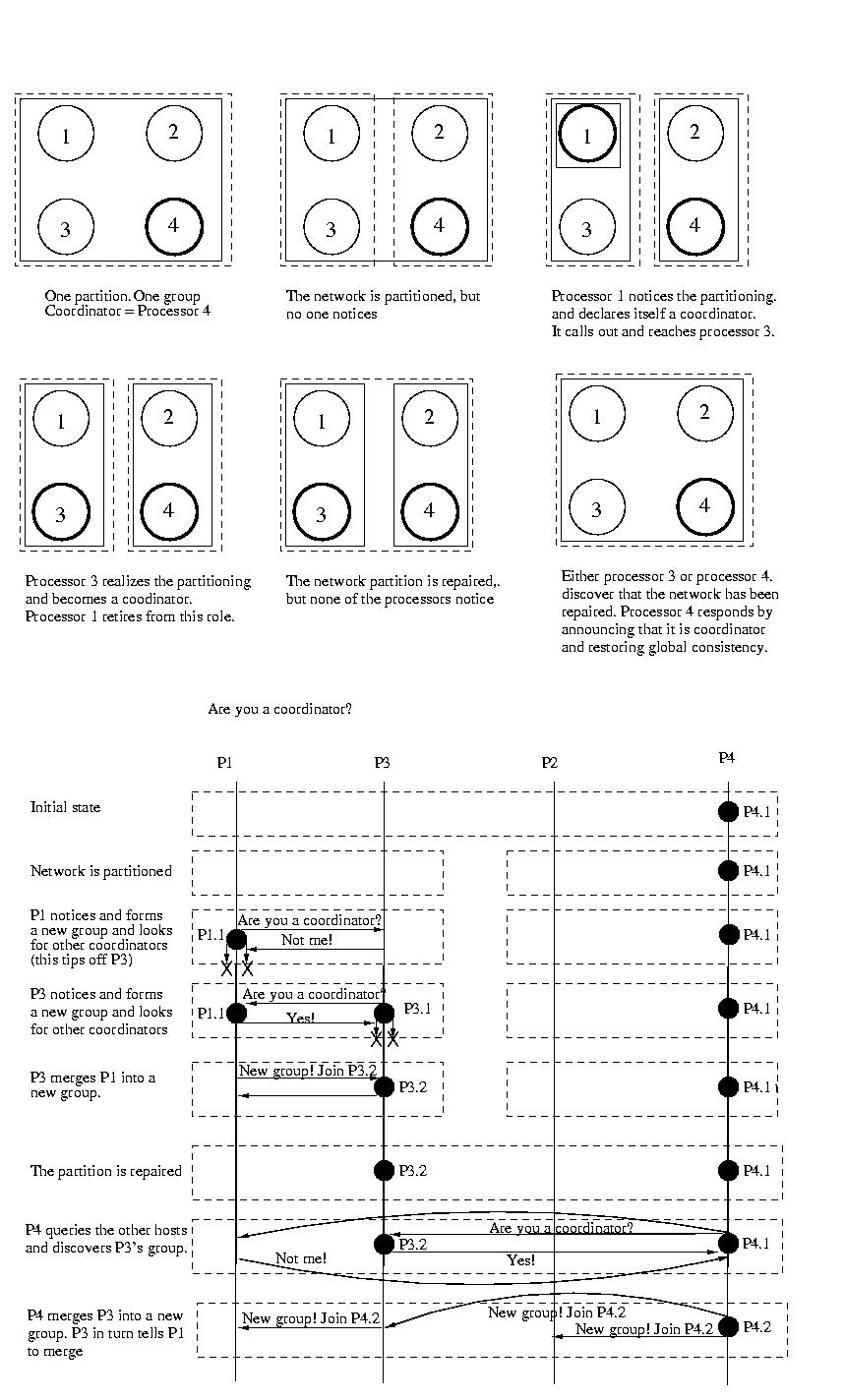
This approach is really very simple. Periodically coordinators look for
other coordinators. If they find other coordinators, they invite them
to merge into a new. If they accept the invitation, the coordinators
tell their participants to move into the new group and move into the
new group themselves. In this way, groups can be merged into a single
group.
As discussed earlier, the state is consistent within a group, but isn't
consistent among groups -- nor does it need to be. This algorithm does not
provided global consistency, just relative consistency -- consistency within
each group. As such, it is useful is systems where this type of
asynchronous processing is acceptable.
For example, a coordinator might ensure that participants attack
non-overlapping portions of a problem to ensure the maximum amount of
parallelization. If there are multiple coordinators, the several groups
may waste time doing the same work. In this case, the merge process would
throw out the duplicate work and assemble the partial results. Admittedly,
it would be better to avoid duplicating effort -- but the optimism might
allow some non-overlapping work to get done.


