Return to the lecture notes index
February 11, 2008 (Lecture 13)
Reading
- Coulouris, et al: 11.2
- Chow and Johnson: 10.1
Token Passing Approaches
At this point, we've considered several different ways of approaching
mutual exclusion: a centralized approach, a couple of timestamp approaches,
a voting approach, and voting districts. Another approach is to create
a special message, known as a token, which represents the right
to access the critical section, and to pass this around among the hosts.
The host which is in possesion can access the shared resource -- the
others cannot. Think of it as the key to the gas station's bathroom.
Since there is only on key, mutual exclusion is ensured.
We'll discuss a few of these approaches. Each will organize the hosts
in a particular way and pass around the token. The diffeerences lie in
how the hosts organize themselves, and perhaps reorganize, themselves,
and the policy governing who gets the token next.
Token Ring Approach
The first among these techniques is perhaps the simplest -- and certainly
among the most frequently used in practice: token ring.
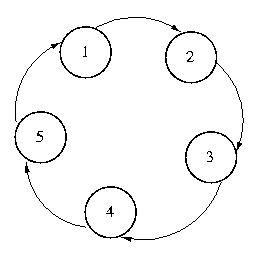
With this approach, every system knows its successor. The token moves from
system to system through the list. Each system holds the token until it
is done with the CS, and then passes it to its successor.
We can add fault tolerance to this approach if every host knows the
mapping for all systems in the ring. If a successor dies, then the
successor's successor, and successor's successor's successor, and
so on can be tried. A host assumes that a system has failed if it cannot
accept the token.
What happens if a system dies with the token? If there is a known time-out
period, the origin machine can regenerate the token and start circulating
it again. Depending on the nature of the CS, this could be dangerous, because
multiple tokens could exist. If only one has access to the resource, this
might be a problem.
The number of messages required per request is very interesting. Under
high contention, the number is very, very low -- as low as one. If every
system wants entry to the CS, each message will yield another entry. But
if no one wants access to the CS, messages will occur for no reason.
But in general, we are more concerned about traffic when congestion is high.
That makes this algorithm particularly interesting. It is especially
interesting in real-time systems, because the worst-case behavior is
well-bound and easily computed.
Raymond's Algorithm
Token ring is very efficient under high contention, but very
inefficeint under low contention. Another way of approaching token-based
mutual exclusion is to organize the hosts into a tree instead of a ring.
This organization allows the token to travel from host-to-host, traversing
far fewer unnecessary hosts.
Raymond's algorithm is one such approach. It organizes all of the nodes
into an unrooted n-ary tree. When the system is initialized, one node
is given the token -- the privlege to enter the critical section. It
may or may not need the privlidge -- but someone needs to have it. The
other nodes are organized so that they form a tree. The edges of this
tree are directional -- they must always point in the direction of
the token.
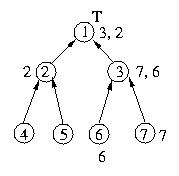
The example below shows an example of a tree initialized for Raymond's
algorithm. Please note that I have drawn it as a binary tree as a force
of habit -- this is not necessary. Another way of describing an
"unrooted n-ary tree" is as "a graph without cycles".
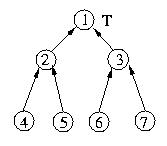
Let's trace the execution of the algorithm through several
requests for and releases of the critical section. Let's begin by
assuming that things are as they appear in the figure above and that
host 1 is within the critical section.
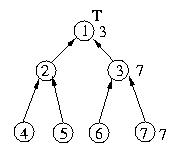
Given these circumstances, the figure below depicts the state of the
system after host 7 requests entry into the critical section.
Process 7 enqueues its own request and then sends a request to host 3.
Process 3 enqueues host 7's request and makes a request as a proxy to
host 1, which in turn enqueues host 3's request.
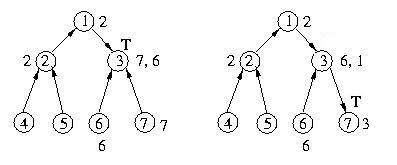
Now let's repeat the process above, this time for a request from
host 2.
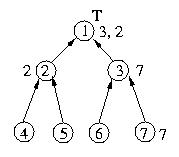
Now, let's see what happens when host 6 requests entry into the
critical section. The big difference in this case is that host
3's queue is not empty. Since host 3 has already requested
the token, it will not request the token again in response to
host 6's request.
Now, let's assume that host 1 exits the critical section. It will
dequeue the first host from its queue of requestors and send the token
to it. It will then set it's current_direction pointer to point to
this node. Once the destination host gets the token, it will set
its current_direction pointer to null, effectively changing the direction
of the edge. Since host 1's queue of requests is not empty, it will send
a message to host 3 requesting the token. This is necessary to ensure
that it can satisfy the enqueued requests.
Once host 3 gets the token, it will dequeue the head of its request queue.
Since the requstor is host 7, not itself, it will send the token to
host 7 and set the current_direction pointer to point to host 7. Since its
queue is not empty, it will send a request to host 7 to ensure that it can
satisfy its pending request from host 2.
When host 7 finishes with the critical section, it will send the token
to host 3, which will in turn send the token to host 6. Host 3 will also
make a request to host 6. This will ensure that it gets the token back
and can satisfy host 1's request.
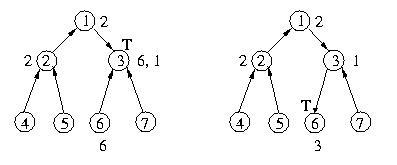
Once Host 6 is done with the critical section, the next chain of
events will send back the request chain through hosts 3 and 1 to
host 2, which will enter the critical section:
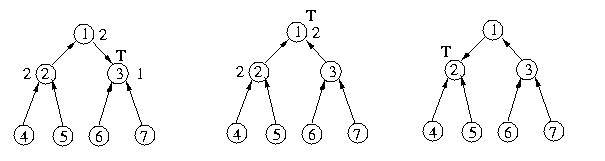
One interesting thing to note about the execution of Raymond's algorithm
is that requests are not necessarily satisfied in the same order in which
they were made. In the example aboce, the requests are amde in the following
order: 7, 2, 6, but granted in the order: 7, 6, 6.
The first time I looked at this algorithm and noticed this property, I
became very concerned. The little robot over my right shoulder was
yelling, "Starvation! Starvation!" I realized that the system does not
have a global queue. It has a collection of local queues. These local
queues are organized using the tree's current_direction relationship,
not FCFS. The result is that local requests are given some preference
over distant requests. Certainly starvation would be possible.
Well, not exactly. Whereas the algorithm isn't fair, starvation cannot
occur. The algorithm does guarantee a maximum path length between
a requestor and a holder. The result is that starvation is not possible.
If you are interested in the proof of this, please drop by -- I'm
happy to go over it with you -- as always, we're here to help.
Path Compression
Raymond's approach limits the number of messages required to obtain access
to the critical section by only communicating with those nodes along the
path between the token and the requestor in the tree, and furthermore by
terminating the request chain as soon as it would begin to overlap another
prior request and as a consequence have no impact.
But, in the worst case, a message could still have to travel all of the way
and down the tree, and the token in the reverse direction -- even if no
intermediate nodes need it. It would be nice if we could simply send the
token to the requestor, without the rest of the scenery.
Path compression, which was originally developed by Li and Hudak for use
with distributed shared memory, allows for this type of "short cut".
It is based on a queue of pending requests. This queue is maintained
implicitly by two different types of edges among the nodes: current_dir
and next.
Each node's current_dir edge leads to its best guess of the node that
is at "the end of the line" of hosts waiting for access to the critical
section. The node "at the end of the line" has this pointer set to
itself.
The next edge is only valid for those nodes that either have the token
or have requested the token. If there is a next edge from node A to node B,
this indicates that node A will pass the token to node B, once it has
exited the critical section. Nodes which have not requested the critical
section, or have no requests enqueued after them, have a null next pointer.
In this way, the next pointer forms the queue of requests. The next pointer
from the token holder to the next node forms the head of the list. The next
pointer from that point forward indicates the order in which the nodes that
have made requests for the critical section will get the token.
The current edge of each node points to that node's best guess about the
last node in the queue maintained by the next edges. Current edges may
be out of date. This is because a node may not be aware of the fact that
additional nodes have been enqueued. But this is okay. A request can
follow the current edge to the "old" end of the queue. This node will
in turn lead to a node farther back in the list. Eventually, the request
will come to the end of the list.
Once a request reaches the end of the current edge chain, it will also be
at the back of the queue maintained by the next pointers, so it can
"get in line" and take its place at the end of the queue.
How do the current edges get updated? Well, as a request is perculating
through the nodes via the current edges, each node's current edge is
adjusted to point to the requesting node. Why? Well the requesting node
is the most recent request and is (or will soon be) at the end of the
request queue.
Let's walk through an example. Let's begin with some unrooted tree
of nodes, giving one the token. The other nodes have current edges that
eventually lead to the token holder. All of the next pointers are null,
since no requests are enqueued.
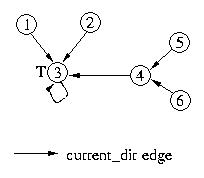
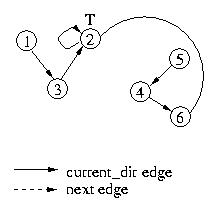
Now, let's see what happens if node 6 requests access to the critical
section. It will forward its request to node 4, and then set its own
current_dir edge to itself to indicate that it is at the end of the list.
Node 4, will forward its request to node 3. Both node 4 and node 3 will
reset their current_dir edges to point to node 6. Since node 3's next
pointer has the token and its next edge is null, it will set its next
edge to point to node 6. This indicates that it will give the token to
node 6 once it is done with the critical section.
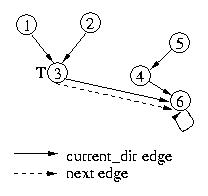
If node 2 makes a request for the critical section, its request will
propogate through node 3 to the end of the current_dir chain. Nodes
3 and 6 will adjust their current_dir pointers. Node 6 will also
adjust its next edge from null to point to ndoe 2. Please note that
the next edges are forming the queue of nodes requesting the critical
section and that the current_dir pointers are being updated as
messages propogate through their origin nodes.
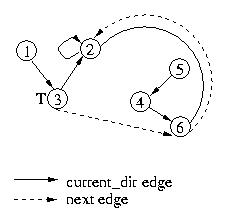
At this point, let's see what happens when node 3 leaves the critical
section. It will pass the token to node 6, and set its own next pointer
to null. Its understanding of the tail of the queue hasn't changed, so
its current_dir edge does not change.
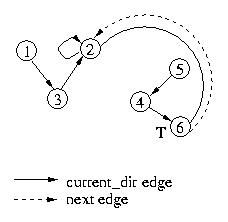
The same process will be followed when node 6 exits the critical section
and passes the token to node 2:
It should be relatively straightforward to see that this approach
reduces the number of messages per request with respect to Raymond's
approach -- we only passed the token to an actual requestor, never
as a simply matter of an intermediate hop.












