Distributed Hashing: Consistent Hashing and Chords

Another idea for a peer-to-peer system is to implement a huge distributed hash table. The problem with traditional hash tables, though, is that they don't handle growth well. The hash function produces a large number, which is then taken modulus the table size. As a result, the table size can't change without needing to rehash the entire table -- otherwise the keys can't be found.

A consistent hashing scheme is one that makes the hash value independent of the table size. The result is that keys can be found, even if the table size changes. In the contest of a distributed hash table, this means that keys can be found, even if nodes enter (and possibly leave) the system.

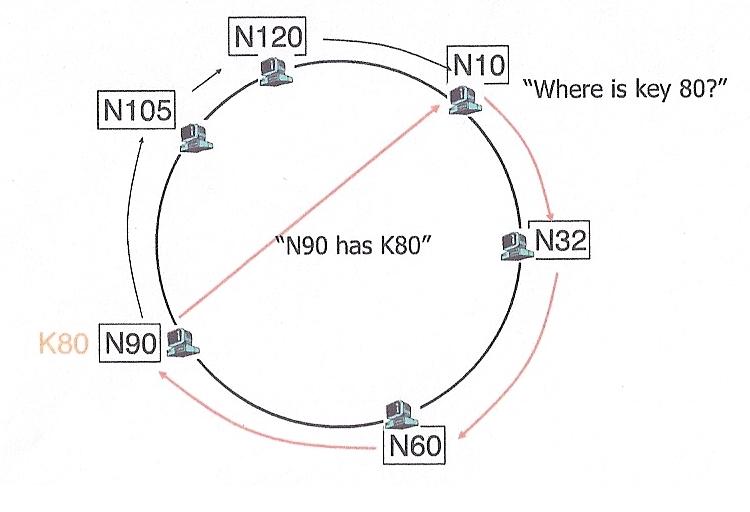
One technique for doing this is the Chord protocol. This protocol views the world as a logical ring. Given an m bit key, it has logical positions 0 ... 2^m-1. Think of them as hours on a clock. Some of these positions have actual nodes assigned to them, others do not. Like token ring, each node "need" only know its successor, but actually knows the topology of the entire ring in order to handle failures.

Since there are fewer nodes than actual addresses (hours on the clock), each node can be responsible for more than one key. Keys are mapped to actual nodes by assigning them to the "closest" node with an equal or greater number.

In order to find a key, we could do a brute fource search of the circle, but instead each node keeps a "finger" pointing to the next node, two nodes away, 4 nodes away, 8 nodes away, etc. In other words, each node keeps pointer to nodes exponentially farther and farther away.

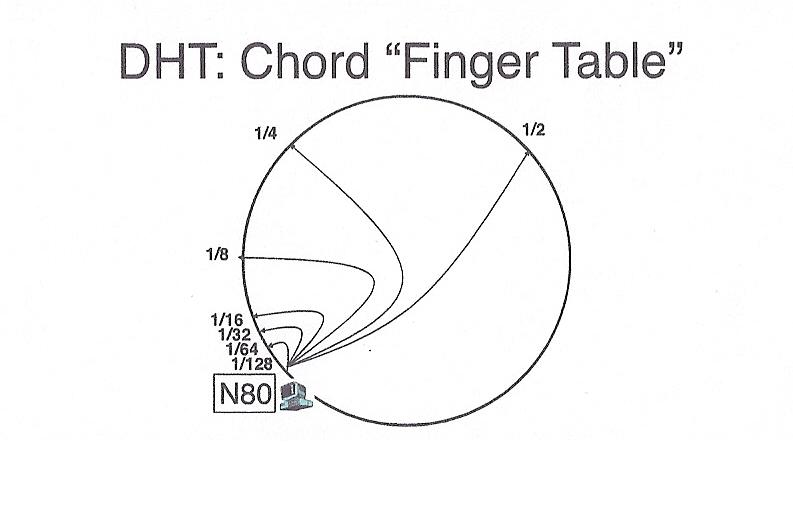
These pointers are stored in a table such that the ith entry of the table contains a pointer to a node that is 2ⁱ away from it, e.g. at position node_number + 2ⁱ. As with keys, if a node is not present at the exact location -- the next greater node is used. This arrangement makes it possible to search for a bucket in O(log n) time, because, with each step, we either find the right node, or cut the search space in half.

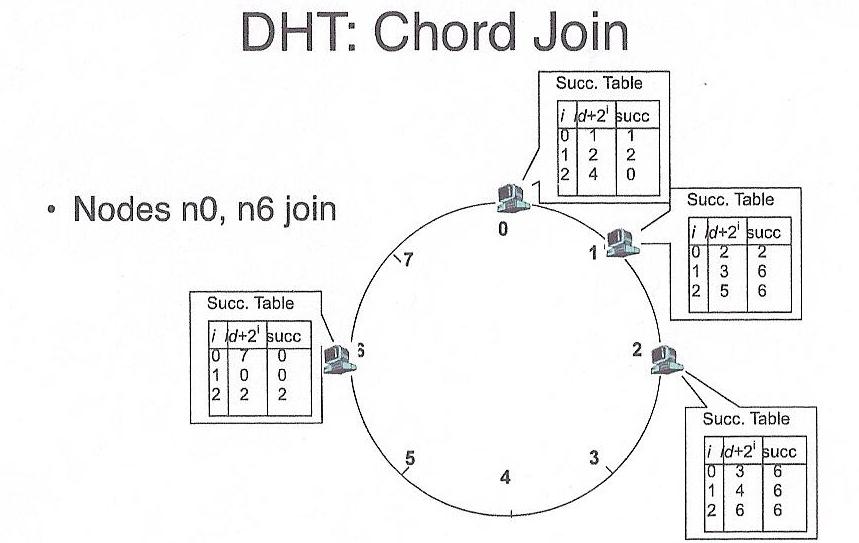
In order for a node to join, it simply is added to an unrepresented position (hour on the clock) within the hash table. It gets its portion of the keys from its successor, and then goes live. Similarly, disappearing from the hash simply involves spilling ones keys to one's successor.

Credit: Thanks to Dave Anderson for these pictures!

LH* (Distributed Linear Hashing)

Linear Hashing is a technique for implementing a growable hash table on disk. Given a hash value, viewed as a binary number, it starts out using one bit, then two bits, then three bits, etc. As the table grows, it uses additional bits. To make sure that the bits maintain their same meaning as the table grows, it uses the bits from right-to-left, instead of left-to-right. This way, as bits are added, they are the more-significant, not less-significant bits. The result is that the one's bit stays the one's bit, and the two's bit stays the two's bit, etc., they don't multiply as more and more bits are used.

The other thing that is interesting is that, when an overflow occurs, it isn't necessarily the overflowing bucket that splits. Instead, overflows are interpreted as an indication that the table should grow, not an immediately fatal condition. Think of them as soft "high water marks", not fatal conditions -- they are resolved locally, somehow. So, when an overflow occurs, the next bucket, in order, splits, adding one more bucket. This is why the algorithm is known as "Linear hashing". The growth is linear.

The "old" bucket knows to which node it split and can provide a reference. Because things "wrap around" the address space eventually catching up with all buckets, the maximum number of redirects is O(log n).

The growth of the table is illustrated below:

It is easy to see that this algorithm lends itself to distributed implementations. Each bucket is a separate node. When an overflow occurs, the overflowing node asks for help, like from a coordinator, but possibly by broadcast or multicast. The new node then get the information about where to split, from the same source, and makes it happen. One distributed implementation is "LH*"

This is a much older approach than the Chord protocol. It is straight-forward for nodes to join -- nodes leaving is, well, not so good.

Distributed Hashing and Fault Tolerance

Fault tolerance is likely managed (a) at the node level, and/or (b) at the system level by replication. To solve this problem, you can more-or-less apply what we've already learned about checkpointing, logging, replication, etc.