Often we hear the terms "Distributed System" and "Parallel System."
What is the difference?
Not a whole lot and a tremendous amount -- all at the same time.
"Distributed System" often refers to a systems that is to be used by
multiple (distributed) users. "Parallel System" often has the connotation
of a system that is designed to have only a single user or user process.
Along the same lines, we often hear about "Parallel Systems" for
scientific applications, but "Distributed Systems" in e-commerce or
business applications.
"Distributed Systems" generally refer to a cooperative work environment,
whereas "Parallel Systems" typically refer to an environment designed to
provide the maximum parallelization and speed-up for a single task.
But from a technology perspective, there is very little distinction.
Does that suggest that they are the same? Well, not exactly. There are
some differences. Security, for example, is much more of a concern in
"Distributed Systems" than in "Parallel Systems". If the only goal of
a super computer is to rapidly solve a complex task, it can be locked
in a secure facility, physically and logically inaccessible -- security
problem solved. This is not an option, for example, in the design of
a distributed database for e-commerce. By its very nature, this system
must be accessible to the real world -- and as a consequence must
be designed with security in mind.
When I teach 15-412, Operating Systems, I begin with a picture
that looks like the one below. If you didn't take OS, please don't
worry -- everything on the picture, almost, should be familiar to
you. It contains the insides of a computer: memory and memory
controllers, storage devices and their controllers, processors, and
the bus that ties them all together.
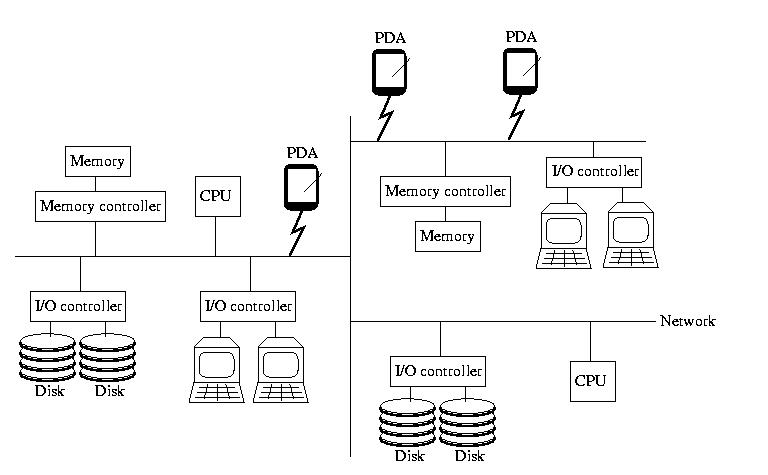
This time however, the bus isn't magical. It isn't a fast, reliable,
predictable communication channel called that always works and maintains
a low latency and high bandwidth. Instead, it is a simple, cheap,
far-reaching commodity network that may become slow and bogged down
and/or lose things outright. It might become partitions. And, it might
not deliver messages in the same order that they were sent.
To reinforce the idea that this is a commodity network, like the
Internet, I added a few PDAs to the picture this time. Remember,
the netowrk isn't necessarily wired -- and all of the components
aren't necessarily of the same type.
Furthermore, there is no global clock or hardware support for
synchronization. And, to make things worse, thr processors aren't
necessarily reliable, and nor is the RAM or anything else. For
those that are familiar with them, snoopy caches aren't practical,
either.
In other words, all of the components are independent, unreliable
devices connected by an unreliable, slow, narrow, and disorganized
network.
Which is preferable, 1 processor, or N processors, each of which is
1/Nth as powerful?
In response to this question, most people point out the following
characteristics:
- Both options are equally "powerful"
- 1 processor is more likely to be completely functional than
N processors, each of which has the same likelihood of failing
as the single processor. If it is "all or nothing", this might
suggest that the single processor is more robust.
- The N processors are less likely to completely fail than the
single processor. In other words, if progress can be made with
only some of the processors, the N processors are "fail soft".
The surprising finding is this: The response time is better for a
system with one processor than N processors which are 1/Nth
as powerful. How can this be possible? Simple math shows:
N*(1/N) = 1.
Let's see if we can think our way through this situation. Let's begin
by defining response time to be the elapsed time between the
arrival of a job and the time that the last piece of the result is
produced by the processor(s). Now let's assume that there is only one
job in the system and that this job is indivisible and cannot be
parallelized. It is fair to assume that the job cannot be divided and
conquered, because any job can be reduced to a piece that is atomic.
This indivisible piece is what we will now consider.
Let's say that this job takes one unit of time in our one processor
system. If this is the case, it will take N units of time if
executed in the N processor system. The reason for this is that the
job can only make use of one processor, so it can only utilize
1/Nth of the power of the N procesor system.
Now if we assume that we have an endless stream of jobs, it might seem
like this problem goes away -- we can make use of all of the processors
concurrently. And, although this is true, it doesn't quite work out
so well in practice. As each job arrives, it must be placed on the
queue associated with one of the processors. Some queues may become
long and other queues may be empty. The backlog that builds up on
the queues that happen to be long is a penalty, whereas the unused
cycles on the available processors offer no reward.
If the arrival rate is less than the service time (which makes sense, if we
hope ever to complete all of the work), we can model the mean response
time for a system with a single processor and a single queue as below:

If you want to try to understand the formula above, you can think of
it this way. Take a look at the denominator of the equation. It
subtracts the arrival rate from the service rate. In other words, it
asks the question, "In each unit of time, if we execute all
of the jobs we have, how many jobs worth of time is left unused?"
If we have another job to submit, we must fit it into this unused time.
The question then becomes, "How many units of time does it
take for me to acquire enough left-over time to execute the new job?"
This subtraction yields the number of fractional jobs that are left
over per unit time, in this case seconds. By inverting this,
we end up with the number of units of time measured that are required
to execute the new job -- this includes the busy cycles that we spend
waiting, and those cycles used ofr the new job.
It might make sense to view this as a periodic system, where each
"unit of time" is a single period. The mean response time is the
mean case for many periods it wil take for use to find enough spare
cycles to complete our job. The piece of each period that already used
represents the cycles spent on th jobs ahead of us on the queue.
Given this, we can model the average queue length as below:

In other words, if the system is at 80% capacity,
L = (0.8/(1-0.8)) = (0.8/0.2) = 4
Again, a quick look at this can give us some intuition about why it is
true. If there are no spare cycles, the load average will be one and
the denominator will be 0, yielding an infinite expected queue length.
If the load average is 0, there are no jobs in the system, so the queue
is empty. If the load average is 80% or 0.8, we can only use 20% or 0.2
of each period for our job. This means that if our job requires 80%
of a period, we will have to wait 4 periods to acquire enough cycles,
hence an expected queue length of 4.
Given this, what happens if, instead of have one processor that has the
power of all N processors? Since it can handle N times as many jobs in the
same time, the service rate is N times greater. Since it is handling
the jobs that were previously spread out over N queues on the same queue,
the arrival rate is N times greater.
following:

Notice the surprising result: We get an N times speedup by having one
processor, instead of N processors that are each 1/Nth
as powerful!
If we service a pool of processors using a single queue, we find our
performance is somewhere in the middle. The service time is much like
having a single very powerful processor, with a single queue, except
the job take longer once it is dispatched, because the processor that
is executing it remains slower. For reference, the figure below shows
all three configurations:
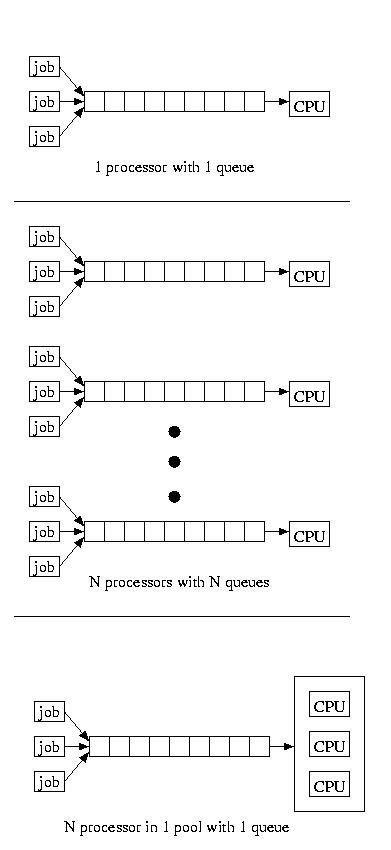
It is a good thing for us that it is cheaper to by N slower processors
than a processor N times as fast -- otherwise distributed and parallel
systems would become less interesting (at least for the purpose of
improving the response time for computationally intensive tasks).
So, although distributed systems might not be useful for reducing the
response times for large, indivisible tasks, they can yield more
processing power for less money, greater availabilty, and greater
accessibility for distributed user communities.




