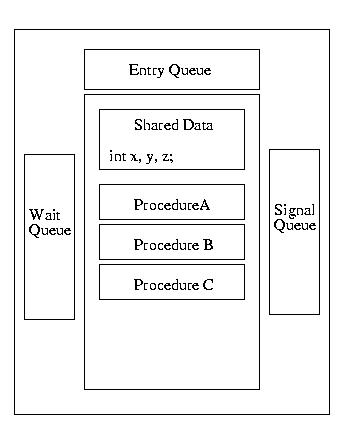
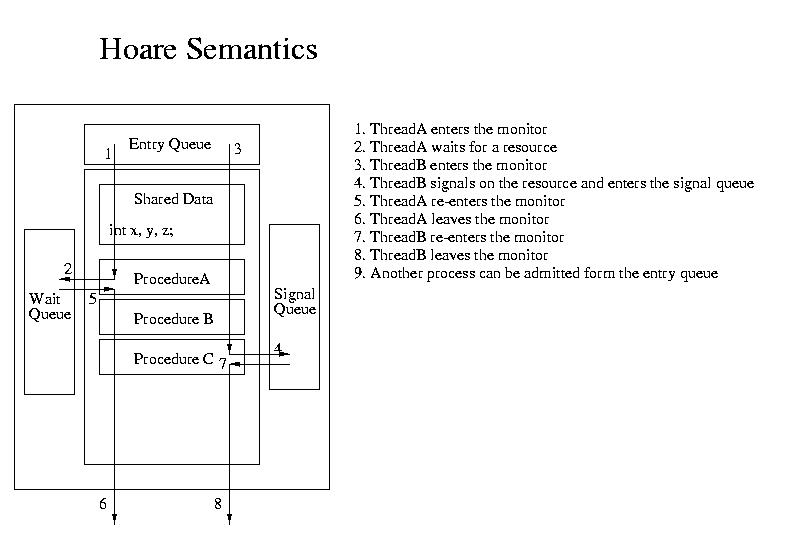
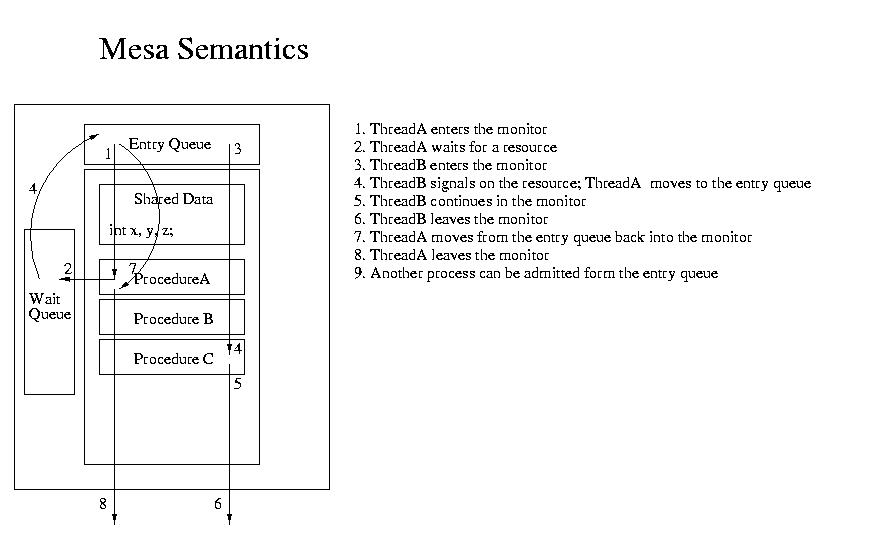
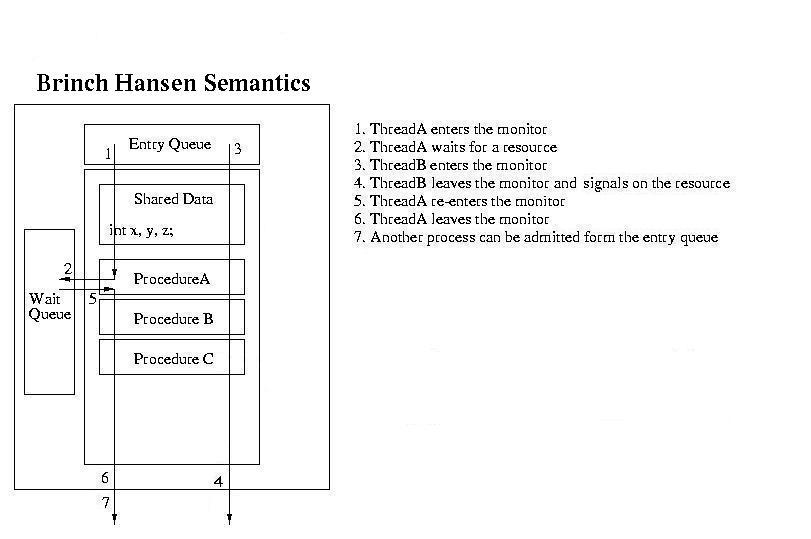
The example below illustrates one of the simplest uses of semaphores. In shows the use of semaphores to protect a crical section. In this case the type of semaphore used is a boolean semaphore. Boolean semaphores can hold values of 0 or 1.
In this case, the semaphore is initialized to a value of 1 and is reduced to 0 by the P() operation when a process enters the critical section. It is incremented back to 1 by the V() operation on exit from the critical section. The P() operation allows a process to atomically enter the critical section and decrement the value of the semaphore to 0. In other words the test of the semaphore's value and decrement of the semaphore value (on entrance) is atomic.
Semaphore x = 1;
while (1)
{
P(x);
<< critical section >>
V(x);
<< Remainder section >>
}
Semantics of Semaphore Operations
The semantics of the semaphore operations are shown below. Please remember that this is intended to describe the behavior of the operations, not their implementation.
It is important to pay attention to the required atomicity within these operations..
The V() operation can not be interrupted during the increment, even though this may take several machine-level instructions to implement.
Furthermore, the test and decrement of x within the P() operation must occur atomically, despite the while loop. But the entire operation cannot execute atomically, because this would require that it occupy the CPU until another thread performed a V() -- this couldn't occur, except on a multiprocessor. The only safe position to context switch within the P() operation is after the test of x within the while loop, but only in the case that loop will repeat. Otherwise the decrement of x must occur before any context switch to protect the atomicity of the test and set of x.
P(x):
while (x <= 0)
;
x = x - 1;
V(x):
x = x + 1;
Bounded Buffering
Another classic problem is the bounded buffer problem. In this
case we have a producer and a consumer that are cooperating through a
shared buffer. The buffer temporarily stores the output of the producer
until removed by the consumer. In the event that the buffer is empty, the
consumer must pause. In the event that the buffer is full, the producer must
pause. Both must cooperating in accessing the shared resource to ensure that
it remains consistent.
A semaphore solution to the bounded buffering problem uses counting semaphores as well as the boolean semaphores we saw earlier. Counting semaphores are a more general semaphore than binary semaphores. The P() operation always decrements the value of the semaphore, and the V() operation always increments the value of the semaphore. The value of the semaphore is any integer, not just 0 or 1. In truth, most implementations provide only counting semaphores. Binary semaphores are obtained through the disipline of the programmer. Even if binary sempahores are provided separately, the result is undefined if P() is called and the value is already 0, or if V() is called when the value is already 1.
The example below shows a general solution ot the bounded buffer problem using semaphores. Notice the use of counting semaphores to keep track of the state of the buffer. Two semaphores are used -- one to count the available buckets and another to count the full buckets. The producer producer uses empty buckets (decreasing semaphore value with P()) and increases the number of full buckets (increasing the semaphore value with V()). It blocks on the P() operation if not buckets are available in the buffer. The consumer works in a symmetric fashion.
Binary semaphores are used to protect the critical sections within the code -- those sections where both the producer and the consumer manipulate the same data structure. This is necessary, becuase it is possible for the producer and consumer to operate concurrently, if there are both empty and full buckets within the buffer.
producer:
while(1)
{
<< produce item >>
P(empty);
P(mutex);
<< Critical section: Put item in buffer >>
V(mutex);
V(full);
}
consumer:
while(1)
{
P(full);
P(mutex);
<< Critical section: Remove item in buffer >>
V(mutex);
V(empty);
}
Bounded wait?
The implementation of semaphores that we've discussed so far doesn't
provided a bounded wait. If two threads are competiting for the
semaphore in ther while loop, which one wins? There is no guarantee
that any thread will eventually win.
This isn't a correct solution -- although problems are rare and require very high contention.
A correct solution needs to have some fairness requirement. The P() operation should add blocked processes to some type of queue. This queue. The V() operation should then free a process from this queue. It isn't necessary that this queue be strictly FIFO, but this is the easiest way to enure a bounded waiting time. It should be impossible for any thread to starve.
The Readers and Writers Problem
The Readers and Writers problem is much like a version of the bounded buffers
problem -- with some more restrictions. We now assume two kinds of threads,
readers and writers. Readers can inspect items in the buffer, but cannot
change their value. Writers can both read the values and change them.
The problem allows any number of concurrent reader threads, but
the writer thread must have exclusiver access to the buffer.
One note is that we should always be careful to initialize semaphores. Unitialized semaphores cause programs to react unpredictibly in much the same way as uninitalized variables -- execept perhaps even more unpredictably.
In this case, we will use binary semaphores like a mutex. Notice that one is acquired and released inside of the writer to ensure that only one writer thread can be active at the same time. Notice also that another binary mutex is used within the reader to prvent multiple readers from changing the rd_count variable at the same time.
A counting semaphore is used to keep track of the number of readers. Only when the number of readers is avalable can any writers occur -- otherwise there is an outstanding P() on the writing semaphore. This outstanding P() is matched with a V() operation when the reader thread count is reduced to 0.
Shared:
semaphore mutex = 1;
semaphore writing = 1;
int rd_count = 0;
Writer:
while (1)
{
P(writing);
<< Perform write >>
P(writing);
}
Reader:
while (1)
{
rd_count++;
if (1 == rd_count)
{
P(writing)
}
V(mutex)
<< Perform read >>
P(mutex);
rd_count--;
if (0 == read_ct)
{
V(writing);
}
V(mutex);
}
Starvation
The solution above allows for the starvation of writers by readers. A similar
solution could be implemented that allows the starvation of readers by writers.
Consider the illustrations below.
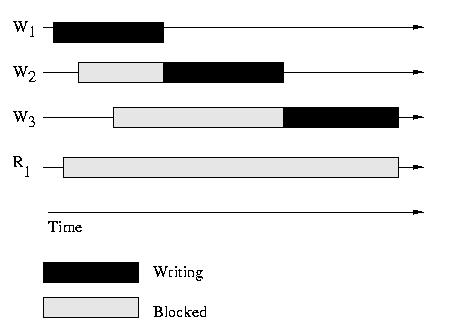
Above: Starved Readers
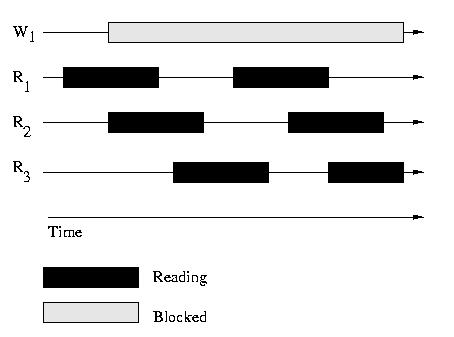
Above: Starved Writers