Today, we talked about various ways of traversing graphs. We start with an algorithm for Topological Sort, which will give us a possible ordering in which the vertices of a directed graph can be vistited. Then, we discuss general methods for traversing a Graph, much like we discussed inorder, preorder, and postorder traversals on trees. Topological Sort

A topological sort is an ordering of vertices in a directed, acyclic (no cycles) graph which travels in one direction only. In order to get a college degree, you must complete a topological sort (ordering) of the required courses, taking prerequisites before you take the coures which build on those prerequisites. Think of the core (or part of the core) curriculum for Information Science.

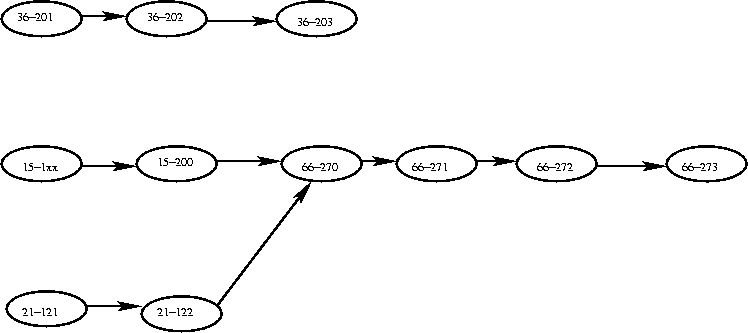
Which vertices have an indegree of 0? The freshman-level courses. Topological sort puts all vertices with an indegree of 0 into a queue.

36-201,	15-1xx,	21-121
  

While the queue is not empty, dequeue.

Dequeue 36-201 and remove it. What happens to the indegree of 36-202? It becomes 0, so enqueue it.

15-1xx,	21-121,	36-202
  

Dequeue 15-1xx and remove it. Now the indegree of 15-200 is 0, so enqueue it.

21-121,	36-202, 15-200
  

Dequeue 21-121 and remove it. Now the indegree of 21-122 is 0, so enqueue it.

36-202, 15-200, 21-121
  

Dequeue 36-202 and remove it. Now the indegree of 36-203 is 0, so enqueue it.

15-200, 21-121, 36-203
  

Dequeue 15-200 and remove it. This does not reduce the indegree of any vertex to 0.

21-121, 36-203
  

Dequeue 21-121 and remove it. Now the indegree of 66-270 is 0, so enqueue it.

36-203, 66-270
  

Dequeue 36-203. This does not reduce the indegree of any vertex to 0.

66-270
  

Dequeue 66-270 and remove it. Now the indegree of 66-271 is 0, so enqueue it.

66-271
  

Dequeue 66-271 and remove it. Now the indegree of 66-272 is 0, so enqueue it.

66-272
  

Dequeue 66-272 and remove it. Now the indegree of 66-273 is 0, so enqueue it.

66-273
  

Dequeue 66-273 and graduate!

How would you implement a topological sort of a graph? You'll need a queue. You'll also need to keep track of the indegree of each vertex in the graph so that you can enqueue vertices of indegree 0. You'll start your algorithm by enqueing every vertex in the graph with an indegree of 0, and your algorithm will terminate when the queue is empty.

Assuming that the indegree of each vertex is stored and that the graph has been read into an adjacency list, we can apply the following (pseudocode) algorithm to generate a topological ordering. Let's assume that the graph is directed and has no cycles.

  void topologicalSort()
  {
    Queue q; //keeps track of what vertex is next (e.g., what course to take next)
    Vertex v, w; //references to Vertex objects
    int counter=0; //keeps track of the topological ordering of the dequeued vertices (e.g., order of courses taken)

    q=new Queue();

    //enqueue all vertices with an indegree of 0 (e.g., courses with no unfulfilled prerequisites
    for each vertex v
      if (v.indegree == 0)
        q.enqueue(v);	
	
      //dequeue vertices one at a time, reducing the indegree of their children as you remove them
      while(!q.isEmpty())
      {
        v = q.dequeue();
        v.topNum == ++counter; //give the vertex you're dequeing its order in the topological sort
	    
        for each w adjacent to v
          if(--w.indegree == 0)
            q.enqueue(w);
      }
    }
	

Spanning Trees

A Spanning Tree is a tree created from a graph that contains all of the nodes of the graph, but no cycles. In other words, you can create a minimum spanning tree from a graph, by removing one edge from any path that forms a cycle.

In the end, this will leave you with another graph, that is also a tree. If this graph contains N nodes, it will contain N-1 edges.

It contains at least N-1 edges, because this many are required to attach each node to the graph. Think of it this way. If the graph contains 1 node, there is nothing to attach it to -- as a result, no edges are needed. If we add nodes to the graph one at a time, we will need to use an edge to attach the new node to the graph. If we add a node, without adding an edge, we've really created a new graph with only one node -- we haven't expanded the old one, because we haven't established a relationship between the new node and any node in the old graph.

It contains at most N-1 edges, because more than one edge per node will create cycles, which would violate the definition of a tree. Imagine that you have a graph, any graph, with the minimum number, N-1, edges. Draw out your imaginary graph.

Now, try to add another edge to your graph, without creating a cycle. You can't do it. The reason is that each node, is already connected to another node of the graph. Adding an additional edge will connected it to a second point on the same graph. As a result, the graph will have a cycle -- it is no longer a tree.

Creating Spanning trees: Traversing Graphs

Today we are going to talk about two different ways of creating spanning trees: the Depth-First Search and the Breadth-First Search. These algorithms are going to be very similar to the algorithms we studied for traversing trees.

The big difference is that we are going to mark the edges as we visit them, and avoid revisiting marked nodes. This is necessary, because graphs may have cycles -- and we don't want to go around-and-around ground we have already covered. So, if we leave a trail of breadcrumbs, and avoid recovering the ground we've already walked.

We can construct a spanning tree by keeping track of the path we follow to reach each node. In other words, we can start out with an empty graph, in addition to the one that we want to traverse. Then, instead of, or in addition to, printing each node we reach during the traversal, we can also add it to the new graph, by creating the same edge that we followed in the traversal to reach it.

So, if we get to Node-X from Node-Y, we then add an edge to Node-X from Node-Y in our new graph. Then, in the end, the new graph has the same nodes as the old graph -- but only one edge connecting each pair.

Depth First Search

Depth First Search (DFS) is a generalization of the preorder traversal. Starting at some arbitrarily chosen vertex v, we mark v so that we know we've visited it, process v, and then recursively traverse all unmarked vertices adjacent to v (v will be a different vertex with every new method call).

When we visit a vertex in which all of its neighbors have been visited, we return to its calling vertex, and visit one of its unvisited neighbors, repeating the recursion in the same manner. We continue until we have visited all of the starting vertex's neighbors, which means that we're done. The recursion (stack) guides us through the graph.

Performing a DFS on the following graph:

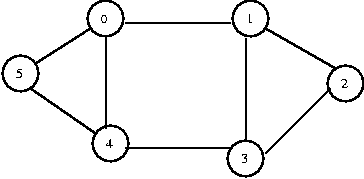
1. Any vertex can be the starting vertex. We choose to visit 1 first. (push 1)
2. From 1, we can go on to 0, 2, or 3.
3. We visit 0. (push 0) [0]
4. From 0, we can go on to 4 or 5 (we've already been to 1). We visit 4. (push 4) [4 0]
5. From 4, we can go on to 3 or 5 (we've already been to 0). We visit 3. (push 3) [3 4 0]
6. From 3, we can go on to 2 or 4 (we've already been to 1). We visit 2. (push 2) [2 3 4 0]
   
   
7. Now we've gone as far as we can go (from 2, we've already visited both 1 and 3). We can start returning.
   
   
8. We return to 3. (pop 2) [3 4 0]
9. We've already been to 1, 2, and 4, so we return.
10. We return to 4. (pop 3) [4 0]
    
    
11. We've already been to 0 and 3, but not to 5. We visit 5. (push 5) [5 4 0] (pop 5, pop 4, pop 0) []
    
    
12. We're done.

Pseudocode for DFS

public void depthFirstSearch(Vertex v)
{
	v.visited = true;
        // print the node or add it to the new spanning tree here
	for(each vertex w adjacent to v)
		if(!w.visited)
			depthFirstSearch(w);		
}

Breadth First Search

Breadth First Search (BFS) searches the graph one level (one edge away from the starting vertex) at a time. In this respect, it is very similar to the level order traversal that we discussed for trees.

Starting at some arbitrarily chosen vertex v, we mark v so that we know we've visited it, process v, and then visit and process all of v's neighbors.

Now that we've visited and processed all of v's neighbors, we need to visit and process all of v's neighbors neighbors. So we go to the first neighbor we visited and visit all of its neighbors, then the second neighbor we visited, and so on. We continue this process until we've visited all vertices in the graph. We don't use recursion in a BFS because we don't want to traverse recursively. We want to traverse one level at a time.

So imagine that you visit a vertex v, and then you visit all of v's neighbors w. Now you need to visit each w's neighbors. How are you going to remember all of your w's so that you can go back and visit their neighbors? You're already marked and processed all of the w's. How are you going to find each w's neighbors if you don't remember where the w's are? After all, you're not using recursion, so there's no stack to keep track of them.

To perform a BFS, we use a queue. Every time we visit vertex w's neighbors, we dequeue w and enqueue w's neighbors. In this way, we can keep track of which neighbors belong to which vertex. This is the same technique that we saw for the level-order traversal of a tree. The only new trick is that we need to mark the verticies, so we don't visit them more than once -- and this isn't even new, since this technique was used for the blobs problem during our discussion of recursion.

Performing a BFS on the same graph:

1. We choose to start by visiting 1. (enqueue 1) [1]
   
   
2. We visit 0, 2, and 3 because they are all one step away. (dequeue 1, enqueue 0, enqueue 2, enqueue 3) [0 2 3]
   
   
3. Because we visited 0 first, we go back to 0 and visit its neighbors, 4 and 5. (dequeue 0, enqueue 4, enqueue 5) [2 3 4 5] 2 and 3 have no unvisited neighbors. (dequeue 2, dequeue 3, dequeue 4, dequeue 5) [ ]
   
   
4. We're done.

Pseudocode

public void breadthFirstSearch(vertex v)
{
	Queue q = new Queue();
	
	v.visited = true;
	q.enQueue(v);
	
	while( !q.isEmpty() )
	{
  		Vertex w = (Vertex)q.deQueue();
                // Pritn the node or add it to the spanning tree here.
  		
		for(each vertex x adjacent to w)
		{			
			if( !x.visited )
			{
				x.visited = true;
				q.enQueue(x);
			}
		}
	}
}