The syntax of the eclaration of a multidimensional array is probably pretty unsurprising. It is basically an extension of the syntax for a one-dimensional array:
int numbers[10]; /* a one-dimensional array */ char names[10][100]; /* a two-dimensional array */ unsigned int cube[10][10][10]; /* a three dimensional array */
And, once declared, the values are accessed exactly as one might expect:
strcpy (names[5], "Greg"); /* 'Greg\0' is stored into the array at row 5 */ names[5][0] = 'G'; names[5][1] = 'r'; names[5][2] = 'e'; names[5][3] = 'g'; names[5][4] = '\0'; cube[2][4][6] = 17;
So, how are multi-dimensional arrays represented within memory? When this question was asked, some folks suggested as arrays of pointers to arrays (of pointers to arrays, of pointers to arrays...). And, this approach could work. But, it isn't actually what C does.
And, there are a few reasons for this. The first one is that managing a data structure that complicated is a bit much for a language feature, especially in a language designed to be as "close to the ground" as C. If arrays were to be implemented that way, especially in a "low high-level language" like C, they'd be implemented in a library, not as a first-class language feature. Second, implementing arrays like that would almost certainly require some form of garbage collection, something C doesn't otherwise have. A call to free() woudl have to do more than free the one pointer it was given -- it would have to play chase. This would be a case of making the comon case slow to support the exception. And the third, which you'll take a closer look at in 15-213, is that scattering arrays in memory, rather than keeping them close together, could, especially for smaller arrays, hurt memory performance.
So, what C really needs to do to keep things fast and simple is to project a multi-dimensional array into a one-dimensionaly memory. And, this is exactly what it does. We'll take a look at the case of a two-dimensional array. But, it extends to higher dimensions, too.
We project a two-dimensional array into a one dimensional array by taking it apart row-by-row or column-by-column. We then place these parts, either rows or columns, next to each other in memory. When we keep rows intact, and place rows, whole, next to each other in memory, this is call row-major ordering. When we break apart the rows, in order to keep the columns intact, and place the columns next to each other in memory, we call this column-major ordering.
Most compilers use row-major ordering. There is no rule about this. But, as it turns out, memory performs better if you use the vectorization that most closely matches the way the data is used. In other words, if the user of the data is most likely to move left-to-right through rows, row-major ordering will perform better than column-major ordering. If, however, the user is more likely to charge up or down columns than across rows, column-major ordering is likely to lead to better memory performance. The reason for this has to do with the way cache memory is managed within the system. You'll learn all about this, and even do some optimization by hand, in 15-213.
Regardless, as it turns out, the most common case of arrays with more than one dimension is arrays with two dimensions. And, when it comes to to dimensional arrays they are more often traversed across ross than up or down columns. As a result, most comilers use row-major ordering.
So, let's take a look at the projection of a two-dimensional array into one-dimensional memory using row-major ordering:
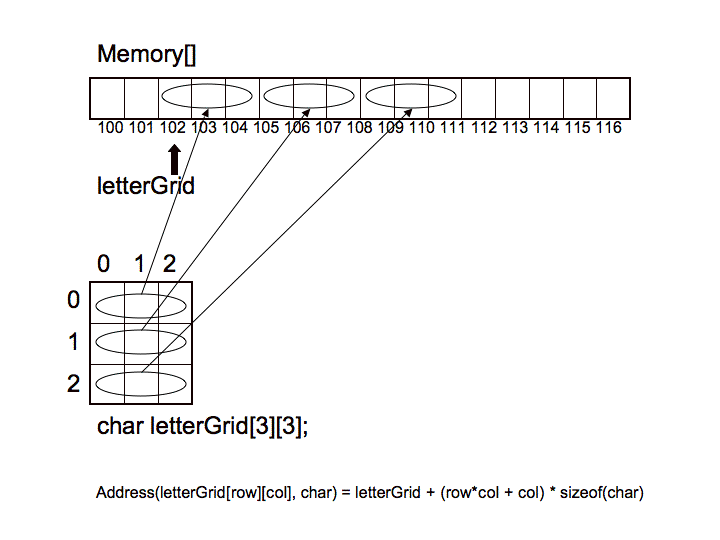
Notice how the 2D array was projected into memory. Take specific note of the formula used to perform the projection:
Address(arrayStart, elementType, #rows, row, col) = arrayStart + (row*#cols + col)*sizeof(elementType)
If we think about it, this formula makes sense because we first move to the beginning of the correct row, by skipping over prior rows, each of which has the prescribed number of columns, and then by moving forward to the correct offset, the correct column position, within the desired row. This is, of course, done in one computation and therefor in constant time. The complexity of the computation is linear with respect to the number of dimensions.