Self-Review Questions

1. Given a sequence of numbers:

   11, 6, 8, 19, 4, 13, 5, 17, 43, 49, 16, 31, 32

   1. Draw a binary search tree by inserting the above numbers from left to right
      
      
      
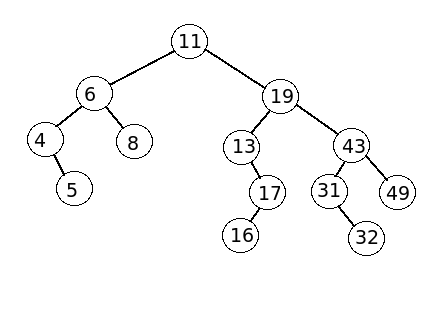
   2. What is the height of the above tree?
      4

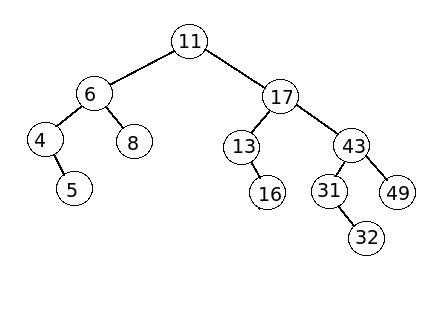
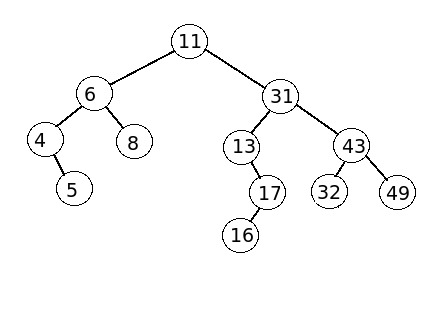
   3. Show the two trees that can be resulted after the removal of 19.
      
      

2. Draw a binary tree T such that
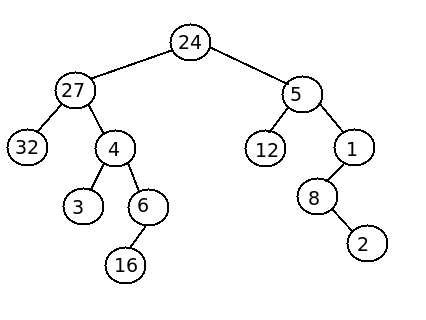
   • each node stores a single number and
   • a preorder traversal of T yields 24,27,32,4,3,6,16,5,12,1,8,2 and
   • an inorder traversal of T yields 32,27,3,4,16,6,24,12,5,8,2,1.
   
   

3. The worst-case runtime complexity of a postorder traversal of a BST with n nodes

a)   O(log n)
b)   O(n)
c)   O(n * log n)
d)   O(n²)
4. Which of the following traversals always gives the sorted sequence of the elements in a BST?

a)   Preorder
b)   Inorder
c)   Postorder
d)   depends on how the elements are inserted
5. The worst-case runtime complexity of insertion into a BST with n nodes is

a)   O(log n)
b)   O(n)
c)   O(n * log n)
d)   O(n²)
6. The worst-case runtime complexity of building a BST with n nodes

a)   O(log n)
b)   O(n)
c)   O(n * log n)
d)   O(n²)
7. The height of a Binary Search Tree with n nodes in the worse case is

a)   O(1)
b)   O(log n)
c)   O(n)
d)   O(n * log n)
8. In a Binary Search Tree, the largest element must

a)   be the root.
b)   be a leaf.
c)   have at least one child.
d)   have at most one child.
9. Given an array of comparable data. How would you sort it using a BST? What is the runtime complexity of this sort?

   Insert the data into the BST then pull it out using an In-Order traversal. The worst-case complexity of the insertions is O(n²). The In-Order traversal is O(n), so the worst-case complexity is O(n²).