Recursive Thinking

Today we are going to talk about a Recursive thinking. Implementations using a recursive programming technique are characterized by functions that call themselves. But, recursive thinking is beyond the mechanics. It is an approach to problem solving that involves remembering the path from the starting position to where you are and using that information to solve a problem. It is also, as importantly, about solving a problem by decomposing it into base cases and cases that tackle part of the problem space.

The Runtime Stack

A stack is a special type of list to which we always add and remove items from the same side. It is called a stack, because, in this respect, it works like a stack of papers -- we can only place a new sheet on top, and can only access the top sheet. Adding an item to the top of a stack is known as a push and removing an item from the top of a stack is known as a pop. One can also peek at the top item, which is equivalent to opping it, looking at it, and pushing it back on.

By now, you probably have notice that, when making function calls, each function gets its own variables, and that, when it returns, the program picks right up where it left off. Python achieves this upon the calling of a function by pushing the return address, arguments, and local variable onto the stack -- and them popping them off, and returning to the popped address, upon returning.

This mechanism is going to prove to be really powerful for solving many problems, because it gives us a clean way of remembering the path from where we started to where we are. This can enable us to, for example, revisit old decisions or systemattically explore or cover space.

The Eight Queens Problem

Backtracking is a typical application of recursion. Sometimes in trying to solve a problem, we speculate -- we take guesses. But guesses can be wrong, so we may want to back up and try again. Since recursion maintains a stack, it is very easy to backtrack using recursion. We can simply return from the current function, back to a previous state, and try again.

In the Eight Queens Problem the goal is to place 8 queens on a chessboard such that no queen can attack any other queen. Queens can attack other pieces on the same row, column, or diagonal.

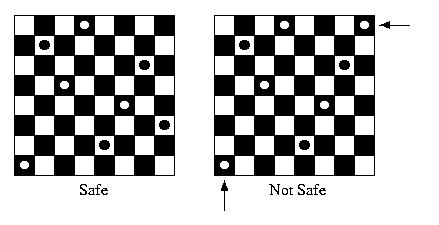
We could try evey possibility -- but that could take 8! = 40,320 tries, even if we did the obvious thing and only placed one queen on each row and column.

Instead, we'll use recursion. We'll speculatively place a queen in each column, starting at the first row, and moving down until it is in a safe position. Then we'll try to place a queen in the next column. And charge forward until we're done (off the board on the other side), But what if we can't charge forward? What if we get to the bottom of the board and haven't found a safe row? Then, there is no safe row in the current column? This means that one of our previous guesses was wrong. So, we return back to the previous level and try the next position. Over the course of the execution, the algorithm may move backward and forward many times, as it discovers wrong guesses and is forced to backtrack.

But, how can we tell if we are returning because we got to the other side of the board and have placed all 8 queens or if we are returning becasue we got to the bottom of a column and couldn't place a queen? The answer is that the return value must be different.

Backtracking

Our approach to the Queens Problem illustrates a problem solving technique known as backtracking. Consider the problems this way. At each stage, we are presented with a collection of options. As a result, we can view the problem as a tree. Our job is to find the path from our starting point, the root, to the solution. To do this, we charge forward along a particular path, until we get to the end, or determine that we cannot. Then, we move backward to the prior decision point and try again. After exporing all of the possibilities there, we back up again. And, if that doesn't work, we back up even farther. Basically, we have a tree. When we approach a collection of branches, we will charge down each in turn. We prefer to go deeper to broader, so this is known as a depth first search.

Regardless, using this approach to solve a problem is known as backtracking and is very naturally implemented using recursion. This is because the runtime stack keeps track of all prior decision points along the current path and which options have been explored. It also ensures that we return to each point in the right order -- the opposite of the order in which we visited them. It does this by returning us to the each function, exactly where we left off in the opposite order in which it was called (as is always the case when a function returns).

The Blobs problem

Assume we have a two-demensional grid of cells. Each cell may be empty or filled. Any group of cells that are connected (horizontally, vertically, or diagonally) constitutes a "blob." The goal is to count the number of cells in a blob, given the location of the blob. You might imagine that the cells have been created by scanning a microscope slide of a bacterial culture, and that the purpose is the estimate the degree of infection. (This problem comes from McCraken's classic textbook -- see the assignment handout for the full citation). This has also been refered to as a forest problem, what part of the forest was burned by the fire.

So, how should you go about solving this problem? The basic idea is this. The recursive method is invoked to determine the number of cells in its blob that are infected. If the cell is not infected or is not in the grid, it should return 0 -- these are the cases that will break the recursion and allow the count to unwind. Otherwise, it should return the sum of 1 for itself, plus whatever is counted by a recursive search of the cells around it. To accomplish this, it should call itself on those cells. We also have to account for the fact that once we count a cell it should have a marker that is changed so that we don't double count cells.

Flood-Fill, More Generally

The Blobs Problem is a specific example of a recursive technique generally known as Flood-Fill. It is called flood-fill, because it is the same technique used within paint programs to fill a bounded area. Think about how the "fill" tool works. It grows outward, just as does our solution to the blobs problem. And, the recursion ends when it goes off the canvas or hits a cell of the "border" color. The code looks exactly the same as our Blobs example above, except for the facts that a) it is marking/coloring the same board as it is processing and b) it isn't counting anything.

What makes flood-fill problems good problems for recursion? Well, what is naturally preserved by the runtime stack that we would otherwise want to preserve with an explicit stack? Int he case of the Queens problem, we were concerned about each decision point in the decision tree and the state of our decision making -- so that we could easily "backtrack" andsystematically try other possibilities.

In the case of flood fill, we are concerned with the location from which we are presently flooding outward. Although the interesting parts of our solution look like one line of code, it is important to realize that there are several recursive calls. And, that these calls are made one at a time, not in parallel. The stack keeps our state in the recursion tree, so we can continue to flood in all directions, rather than just following one path away. This is important, because the flood-fill appracoh relies on exploring in all directions, making this state information critical.

The Power of Recursion

In general, recursion is a good solution to a problem, if:

• The solution requires recursive thinking, e.g. a stack that can easy be managed by function calls and returns
• The problem is most easily expressed recursively, for example when it maps closely to a mathematical statement of the problem or a description of an algorithm that is naturally expressed using recursion
• When we want to prove properties by induction, as recursive expressions of the problem are structured much like inductive proofs

In general, unless there is a reason to favor recursion, we should avoid it, as recursive solutions spend time making function calls, which are costly, as, for example, they need to push data onto and pop data off of the stack. Unless this data is important to us an easily accessed as a stack, or the problem is better expressed recursively at a human level -- it probably isn't worth the cost.