A heap is a data structure that is basically a tree. It is specifically a full and complete binary tree, and must be added from left to right. Its only other property is called the 'heap ordering property', which means that its parent is less than its children. We have to make sure that we keep this property every time we insert.

You can think of a heap as a tree, but the most efficient way to implement it is with an array.

      1
    /   \
  3      2
 / \    / \
5   6  4   7 

can be in an array as [1, 3, 2, 5, 6, 4, 7].

Inserting Into A Heap

When we insert into a heap we need to make sure that the resulting structure is still a heap. So the resulting structure needs to maintain the relationship between each node and its children, and the resulting tree cannot have any holes in it anywhere except for the bottom right of the tree. We will always initially use the first available spot (the leftmost open spot at the bottom of the tree) to initially insert the new item into the heap, so the tree will continue to be full after we insert. But will it still be a heap?

Let's look at an example of constructing a min-heap:

We will begin by inserting 70 into the heap. Since this is the first item in the heap, it will have to be the root.

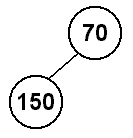
Next, we will insert 150 into the heap. Since the tree is full at depth 1 (the root), we will insert it in the leftmost spot at depth 2, which in this case is the root's left child. Since 70 < 150, this is still a heap.

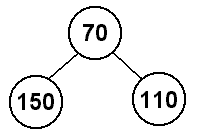
Now we will insert 110 into the heap. The next available spot to add an item to the heap is roots right child, so we will add 110 there. This is also still a heap because 70 < 110. (Remember, it does not matter how the siblings relate to each other.)

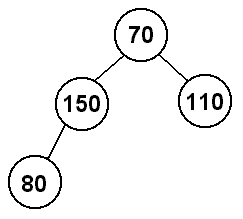
Next, we will insert 80 into the heap. Since the tree is now full at depth 2, we will add 80 at the leftmost spot at depth 3 (150's left child). This presents a problem, though, because 150 > 80, so we no longer have a heap.

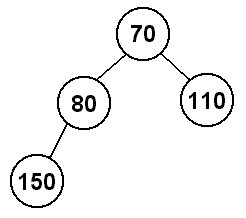
How do we make this a heap again? Whenever we insert, we have to look at the new node's parent and check the relationship. If the new node is smaller than its parent (in a min-heap), then we will swap the two values. After we have done this, we then have to check if the new one is smaller than its new parent. We continue this process of checking and swapping until we either hit the root or reach a spot where the new value is greater than its parent, because in either case we will have a heap again.

So, when we insert 80, we will have to swap it with the 150 since 150 > 80. 80's parent will now be 70, so we will stop there since 70 < 80.

Now let's add 30 to the heap. This will start in the second spot at depth 3 (80's right child), and then will have to swap with 80 because 80 > 30, and then will also swap with 70 because 70 > 30, so here 30 will become the new root of the heap. This is consistent with our idea of a min-heap, since 30 is now the smallest value in the heap.

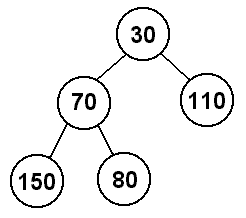
Finally, we will add 10 to the heap. It will start in the third spot at depth 3 (110's left child), and we will have to swap it with 110 because 110 > 10, and then we will also have to swap it with 30 because 30 > 10, so now 10 becomes the root of the heap.

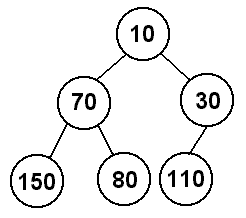
So, when we insert something into the tree, we initially place the item in the bottom, leftmost spot in the tree, and then swap the new value with its parent until we once again satisfy the properties of the heap. Which is the minimum element of the array? We are gauranteed that it is the first element, at the 0th index. If we remove it, though, we have a hole. How do we fill it?

Removing From A Heap

When we remove an item from the heap, we will always take the value at the root. Why? The reason we use a heap is to have easy access to the item that has the highest or lowest value in the current set of items. Like the stack and the queue, limiting the possible behavior of the heap ensures that it will behave consistently.

When we remove the item at the top of the heap, we leave an empty spot. Since the heap cannot have any holes in it except at the bottom-right, we no longer have a heap, so what can we do to reestablish a heap?

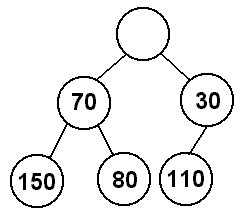
Our first concern is that the root of the heap gets the lowest value in the tree. Luckily, we can narrow our search for that value to the root's children. Why can we do this? Well, we know that in a min-heap the parent has a smaller value than its children, so all of the values below root's left child must have a greater value than root's left child, and all of the values below root's right child must have a greater value than root's right child. This means that the minimum value in the heap will be either root's left child or root's right child. That means we can promote the minimum of root's children to the root of the heap.

In this case, that means that 30, the right child of the root, will be moved to the top of the heap.

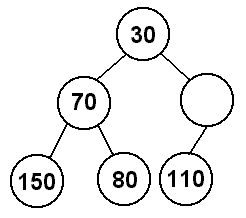
Now there is a hole where the 30 was, so we will again have to move one of its children up the heap. Since there is only a left child, 110, we will move that to where 30 was.

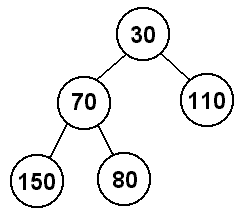
We are left with a tree that satisfies the properties of the heap, so we are done. Unfortunately, it is not always this easy. Suppose we have the following heap:

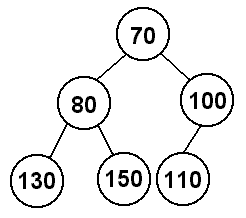
If we remove the minimum value, the 70, we will replace it with the 80, and then replace the 80 with the 130. That would leave us with:

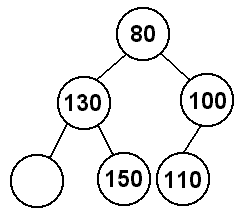
The tree we are left with is not a heap, because there is a hole on the bottom left of the tree. So what should we do in this situation? Well, if we are going to have holes in the tree, they should be at the bottom of the tree and to the right of all the values. To fill in this hole, then, we will take the last value in the heap (the bottom rightmost value) and move it to where the hole is.

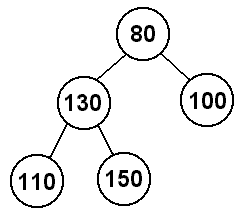
We've gotten rid of the hole, but now the relationship between parents and children is not maintained because 130 > 110. So, after we fill in the hole, we have to once again move up the tree swapping with the parent until the parent is smaller.

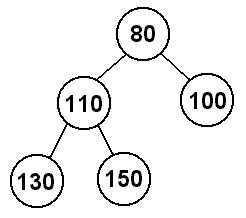
Now, we finally have a heap. To review, first we remove the value from the root of the heap, and then work our way down the tree replacing the removed value with the smaller of the two children. Next we move the last value in the heap to fill in the hole (if there is a hole). Finally, we swap up the tree like we did in the insert so that the tree we are left with still satisfies the properties of a heap.

What is the running time of this algorithm? The insert included adding it first at the end, which is constant time, and then swapping with each of its parents as necessary to maintain the property. There are log(n) parents, so in the worst case, there are O(log(n)) steps in the insert.

We insert n elements, each of which take O(log(n)) time, so that would be O(n*log(n)) to actually build the tree.

How expensive is it to removeMin? To find the min, it is constant time because we know the insert is always at index 0. However, to remove it, we have to swap with at most log(n) elements to maintain the heap order property. We do this for n elements, so that is also O(n*log(n)).

Heapsort is a combination of building and removing, so O(n*log(n)) + O(n*log(n)) = 2*O(n*log(n)) = O(n*log(n)). We have successfully avoided an O(n^2) running time, and instead have a worst case of O(n*log(n)).

How can we get the parent or child of a node? Integer divison makes it very easy. For the above transformation:

      1
    /  \
  3      2
 / \    / \
5   6  4   7 

to

[1, 3, 2, 5, 6, 4, 7]

we can see that the 0th index's children are at index 1 and 2, and the 4th index's parent is at index 2. In general, it actually works out that for a node n, its parent is at n/2 and its children are at 2*n + 1 and 2*n + 2.

To maintain the heap ordering property, we just have to compare nodes with parents and children, which we can now easily do.

If you notice, we're creating an ordered list ending up with [7, 6, 5, 4, 3, 2, 1], because our removeMin takes the first index and swaps it with the last element, building an ordered list starting at the right. If we wanted to have a list from smallest to largest, we could just reverse our heap order property, and change it so that the parent must be greater than its children. Then we would do a removeMax instead, and adding the max at the end each time.

How do we know that the insert and removeMin are O(log(n)), having log(n) growth?

2^1 - 1 total nodes                   a
2^2 - 1 total nodes            b          c
2^3 - 1 total nodes         d      e    f     g
2^4 - 1 total nodes       h   i  j  k  l m   n o

If we had to do a percolation for a heap with 2^n nodes, it would take around n-1 swaps. For any general n, it would take approximately log-base2 (n), which we can just treat as O(log(n)) time.

Trees are just data structures that have a parent/child relationship. The children at the very bottom of the tree is called a leaf, or more specifically a node with no children. The node at the top of the tree with no parent is called a root.

There are often many relationships between the parents and children, in the heap case, we have it such that the parent is always less than its children.

We will now introduce what is called a Binary Search Tree, which has a property that everything to the left is greater than its right.

If we have a list 7, 4, 8, 12, 13, 1, 5. We start out with 7.

7

We now insert 4, which is less than 7 so we insert it to the left

    7
  /
4

We now insert 8, greater than 7 so we insert it to the right.

 
    7 
  /   \ 
4      8

Inserting 12, we see is greater than 7, and also greater than 8.

  
       7 
     /   \ 
   4      8
           \
            12

13 we see is greater than 7, and also greater than 8, and also 12.

  
       7 
     /   \ 
   4      8
           \
            12
             \
              13

If we insert 10, we see 10 > 7 so move right, and 10 > 8 so move right again, but 10 < 12, so we insert it into 12's left subtree, giving:

  
       7 
     /   \ 
   4      8
           \
            12
           /  \
          10  13

Let's construct a binary search tree using by inserting the letters of "HELLO WORLD" into the tree one at a time. For convenience, we will ignore duplicate letters.

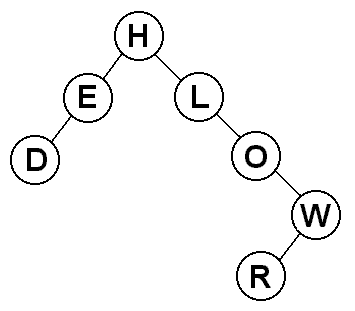
How did this work? Let's go through the string one letter at a time.

• "H" - the tree is initially empty, so "H" becomes the root
• "E" - "E" comes before "H", so it goes on the left
• "L" - "L" comes after "H", so it goes on the right
• "L" - "L" is already in the tree, so we ignore it
• "O" - "O" is greater than "H", so it goes to the right of it, and it is greater than "L", so it goes to the right of that, too
• "W" - "W" is greater than "H", so it goes to the right of it, it is greater than "L", so it goes to the right of that, and it is greater than "O", so it goes to the right once again
• "O" - "O" is already in the tree, so we ignore it
• "R" - "R" comes after "H", "L", and "O", so it goes to the right of all of them, and then it comes before "W" so it goes to the left of it.
• "L" - "L" is already in the tree, so we ignore it
• "D" - "D" comes before "H", so it goes to the left of it, and it also comes before "E", so it goes to the left of that, too.

The result is the tree you see. If you look at any node in the tree, you will see that the binary search tree ordering property holds. As as aside, unlike heaps which only provided a partial ordering, binary search trees provide a full ordering. However, what if we get the list 1, 2, 3, 4, 5, 6. Insert 1 1 Insert 2 1 \ 2 Insert 3 1 \ 2 \ 3 ... We end up with: 1 \ 2 \ 3 \ 4 \ 5 \ 6 We have succeessfully made a linked list. Just like our quicksort, or binary search when fed badly can perform very poorly. As is, we have no gaurantee that we will perform perfectly. We can't perform a nice array representation of the binary tree as we did with a heap, because we can have a huge waste of space if it's very sparse. To solve this, we have a Node class, much like we did for the Linked List.

class Node {

  private Comparable data;
  private Node left;
  private Node right;

  ...
}

What is this Comparable? Comparable is an interface specification, with this simple definition:

interface Comparable { 

   public int compareTo (Object o);
   
}

Any class that implements this compareTo() method can say that it 'implements Comparable'. For example, the String class is declared as:

class String implements Comparable { 

This means that the String class has everything that the Comparable interface expects, and Java will enforce that.

Having an object of type Comparable means that the data must implement the Comparable interface, so you can say something like:

Comparable c = new String("Hi mom");

Since Strings implement Comparable, Java will allow this and just treat the String as if it were a Comparable.

The compareTo() method simply does a compare as follows, so if you have dog1 and dog2, and call the method as:

dog1.compareTo(dog2)

This essentially does an implementation of dog1 - dog2. If dog1 is greater than dog2 (by some sort of comaprison) then it would return a positive value, and if it is less than dog2 then it returns a negative value.

Now you have been introduced to everything necessary for the mastery exam. You are given two sets of LinkedList questions and two sets of BinaryTree questions, which you should do before the mastery exam so there are no surprises when you are asked to write the methods.

The questions for both can be found at:

http://courseweb.sp.cs.cmu.edu/~finalexam/

You will be given the classes that are provided. Be sure to look at them many times. You should be able to know exactly what you can and cannot do.

The given insert for the BST is below:

  public void insert(Comparable data)
  {
    if (null == data)
      return;
    
    root = insert(root, data);
  }

All of the main work is done in a recursive helper method seen below.

  private BSTNode insert(BSTNode root, Comparable data)
  {
    if (null == root)
      return new BSTNode(data);
    
    if (root.getData().compareTo(data) == 0)
      return root;
    
    if (root.getData().compareTo(data) > 0)
      root.setLeft(insert(root.getLeft(), data));
    else
      root.setRight(insert(root.getRight(), data));
    
    return root;
  }

How does this recursion work? If the root is null, then it just sets the root to a new BSTNode with the data. If it's not null, then it does different things based on the comparison of the current root and the data to insert. Notice that insert returns a BSTNode, which you assume is the result of inserting the new Node. Binary search trees can't handle the case easily of if the data and the root are equivalent, so it just returns the root if the data already exists in the tree. If the data to insert is less than the data of the root, then you want to setLeft() the root to the result of the inserting of the data at root.getLeft(). In effect, you're transferring the responsibility over to the left subtree to insert it. The same goes for the right subtree.

How would a simple find method work? We can easily do this with a for loop, just manipulating the tempNode to go left or right based on its compareTo() to the tempNode. If it's equal you return, else just go left or right.

How about a remove method? Suppose we have a tree given below:

             7
          /      \
       5           13
      / \        /     \
    2    6      8         16
   /             \       /   \
  1               10    14    18
                  /\     \    
                 9  11    15 

What happens if we want to remove 13? We have two options, the rightmost node in the left subtree or the leftmost node in the right subtree. It doens't matter which you take. For this example, we will replace it with the leftmost of the right subtree.

Since it's the leftmost of the right, we know it has no left subtree or else its left subtree would be be the leftmost. Therefore we can just set replace it with its right subtree. In this case we have 14 as the leftmost of the right subtree, so we replace 13 with 14 and then in place of 14 we put its right subtree, 15.

             7
          /      \
       5           14
      / \        /     \
    2    6      8         16
   /             \       /   \
  1               10    15    18
                  /\       
                 9  11