Return to the Lecture Notes Index
15-111 Lecture 26 (Friday, April 6, 2007)
Finding a Minimum Spanning Tree of an Undirected, Connected Graph
A minimum spanning tree of an undirected graph is a tree formed from that
graph's edges that connects all the vertices of that graph at the lowest total
cost. You can make a spanning tree of a graph only if the graph
is connected. There may be more than one spanning tree of a particular
graph.
The number of edges in a minimum spanning tree of a graph will be the number of vertices it has - 1. A minimum spanning tree is a tree because
it's acyclic. It's spanning because it reaches every vertex in the
graph, and it's minimum for the obvious reason. If we need to wire a
house with a minimum of cable, then a we need to find a minimum spanning
tree of a graph of the electrical layout of the house.
Minimum Spanning Trees: Why Do We Care?
Many real situations can be modeled with graphs. And, many real situations
can be solved by finding the minimum spanning tree of graphs.
My favorite example involves an electrician and a house. Imagine that
a collection of electrical outlets have been installed in the walls
of a house, and that the electicity enters the house at a single electrical
box. We can model this situation as a graph, where each of the outlets
and the electrical box is a node, and the walls are the edges. The
length of each wall, or segment thereof, is the distance along the wall
between two of the electrical connections.
As a result, the electrician may have many different routes he can use
to wire the outlets -- they may be reachable by different paths along the
walls. So, the electrician wants to find the path that requires the least
amount of wire. This saves money, becuase less wire is needed. And, it
saves time, because the runs along the wal are shorter and, as a consequence,
take less time to install.
To solve this problem, the electrician can model the outlets and wall
segments conecting them as a graph rooted at the electrical box. Then,
the electrician can find the minimum spanning tree of the graph. The
edges in this tree give the paths that the electrician should use to
run the wires -- they will reach each node, while requiring the least
amount of wire.
Prim's Algorithm
Imagine finding the minimum amount of sidewalk needed to get to every
point of interest from the entrance of a park. Now think of the park
entrance as the root of your minimum spanning tree. This will help you as
you apply Prim's Algorithm.
Prim's grows the tree in successive stages. You start by choosing one vertex
to be the root v, and add an edge (piece of sidewalk), and thus an
associated vertex (a point of interest in the park), to the tree. At each
stage, you add a vertex to the tree by choosing the vertex u such
that the cost of getting from v to u is the smallest possible
cost (in the case of the park, the cost is distance). At each stage,
you say, "Where can I get from here?" and go down the shortest road possible
from where you are.
Applying this algorithm until all vertices of the given graph are in the tree
creates a minimum spanning tree of that graph. This may sound familiar. Prim's
algorithm is essentially the same as Dijkstra's -- with a different cost
function. They both proceed using the same greedy strategy.
Prim's finds the minimum spanning tree of the entire graph from s, so we
use the Length field to record the cost of getting from a vertex v to
its parent in the minimum spanning tree we're making.
Suppose we have the following graph:
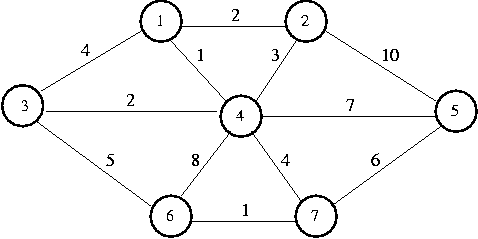
We would build a table as follows:
|
| Known
| Path
| Length
|
| 1
| -
| -
| INF
|
| 2
| -
| -
| INF
|
| 3
| -
| -
| INF
|
| 4
| -
| -
| INF
|
| 5
| -
| -
| INF
|
| 6
| -
| -
| INF
|
| 7
| -
| -
| INF
|
Selecting vertex 1 and making it the root of our tree, we update its
neighbors,
1, 2, 3, and 4. Vertex 1's cheapest place in the tree is known.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| -
| 1
| 2
|
| 3
| -
| 1
| 4
|
| 4
| -
| 1
| 1
|
| 5
| -
| -
| INF
|
| 6
| -
| -
| INF
|
| 7
| -
| -
| INF
|
Next we select vertex 4 (one of the neighbors of vertex 1). It's
cheapest place in the tree is now known. Every vertex in the graph is
adjacent to 4.
Vertex 1 is known (meaning that its in its optimal place in the tree),
so we don't examine it. We don't change vertex 2, because its Length is
2, and the edge cost from 4 to 2 is 3. We update the rest.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| -
| 1
| 2
|
| 3
| -
| 4
| 2
|
| 4
| Y
| 1
| 1
|
| 5
| -
| 4
| 7
|
| 6
| -
| 4
| 8
|
| 7
| -
| 4
| 4
|
Next we select vertex 2 (another neighbor of 1) and make it
known. We can't improve our tree in any way by going through vertex 2.
We select vertex 3 (the last neighbor of 1) and make it known.
The path from 3 to 6 is cheaper than the path from 4
to 6, so we update 6's fields.
2 and 3's cheapest places in the tree are now known.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| Y
| 1
| 2
|
| 3
| Y
| 4
| 2
|
| 4
| Y
| 1
| 1
|
| 5
| -
| 4
| 7
|
| 6
| -
| 3
| 5
|
| 7
| -
| 4
| 4
|
Next we select vertex 7 (neighbor of 4, the first chosen neighbor
of 1). Its cheapest place in the tree is now known. Now we can adjust
vertices 5 and 6. Selecting 5 and 6 doesn't
provide any cheaper paths. After 5 and 6 are selected, the
Prim's algorithm terminates.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| Y
| 1
| 2
|
| 3
| Y
| 4
| 2
|
| 4
| Y
| 1
| 1
|
| 5
| Y
| 7
| 6
|
| 6
| Y
| 7
| 1
|
| 7
| Y
| 4
| 4
|
To find the minimum spanning tree of the graph featured in the table, follow
the Path fields from vertex 1.
Kruskal's Algorithm
Now that we've discussed Prim's Algorithm, we are going to discuss a second
approach for solving the same problem. This approach is also a greedy
algorithm.
Although the implementation is a bit more complex, the basic algorithm is
very straight-forward. We simple attempt to add each edge from the original
graph to the minimum spanning tree, beginning with the lowest-weight edge and
finishing with the greatest-weight edge. We add the edge if it doesn't cause a
cycle and passs it up, if it does. We continue to add edges, until we've
added N-1 edges, where N is the number of verticies. Remember, spanning trees
have exactly N-1 edges -- never more, never less.
This works for more-or-less the same reason that Prim's Algorithm works. We
need to add n-1 edges to the graph. Adding the smallest n-1 legal edges to
the graph is guaranteed to give us the spanning tree with the least aggregate
weight. Since we don't add an edge if it creates a cycle, we know we'll have
a tree. Since we add exactly n-1 edges, we know that it will be a spanning
tree -- one less and it would be disjoint trees, one more and it would be
a more general graph with a cycle. And, since we add the smallest such edges,
we know it has the lowest total weight. And, it all works out, because it
is never the case that adding a more costly edge earlier would prevent
a cycle allowing the addition of super-cheap edges later.
In order to make it easy to select the candidates in the right order, from
the lowest weight to the highest weight, we store the edges in a
priority queue (heap). Then, selecting an edge is simply the
deleteMin() operation.
Another way of viewing the algorithm is to views the inital
configuration as a forrest of trees, with each vertex in its own, independent
tree. If we take this view, then adding an edge merges two trees into one.
When Kruskal's terminates, there is only one tree - the minimum spanning tree.
Let's take a look at the algorithm in operation, using the same graph as
we used last class:

The following table shows the verticies sorted by weight and whetehr or not each vertex
was accepted. Remember, we evaluate each vertex, one-at-a-time, from the top of this list
down. In a real implemention, we would have added them to a heap, and be using deleteMin()
to get to the top one for each iteration.
| Edge
| Weight
| Action
|
| (1,4)
| 1
| Accepted
|
| (6,7)
| 1
| Accepted
|
| (1,2)
| 2
| Accepted
|
| (3,4)
| 2
| Accepted
|
| (2,4)
| 3
| Rejected
|
| (1,3)
| 4
| Rejected
|
| (4,7)
| 4
| Accepted
|
| (3,6)
| 5
| Rejected
|
| (5,7)
| 6
| Accepted
|
Using Sets to Detect Cycles
So, how can we figure out if adding a particular edge to a tree will create a
cycle? This is very important to Kruskal's Algorithm, because we only add an edge,
if doing so won't create a cycle.
Imagine that each vertex in a graph is its own set (remember the
Set class you created for the lab?).
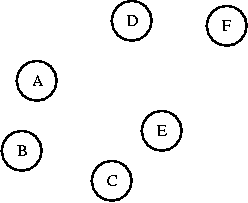
If you connect two vertices in the same set together, you'll create
a cycle. As long as you connect vertices from two different sets, you
won't create a cycle. A and B are in different sets. I'll connect them.
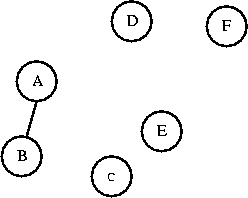
Now AB is a set. Can I connect C to AB? C and AB are in different sets,
I'll connect them. Now I have a set called ABC.
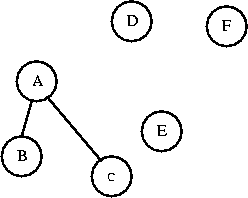
Can I connect C to B? C and B are in the same set, so connecting them
will create a cycle.
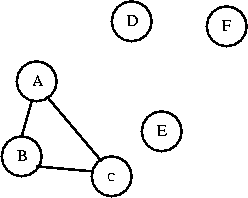
Union-Find
Imagine a graph, with each vertex as its own set. Now imagine that
each set of vertices is a tree. So before we connect any edges, each vertex
is its own tree, and the graph is a forest of trees. What we need to
do is develop a fast way to perform the union and find operations upon
sets of edges.
We'll use an array to represent the trees. Create an array, with each
index of the array representing the corresponding vertex of the graph.
Place a sentinel value, -1, into each array element. We will use this
sentinel value to denote the root of the tree. Before we connect any edges,
each vertex is its own tree, so its the root. -1 represents the root of the
tree set.
0 1 2 3 4 5 6 7
[-1] [-1] [-1] [-1] [-1] [-1] [-1] [-1]
Now I decide to connect 7 to 1. They are in different sets, so I connect them.
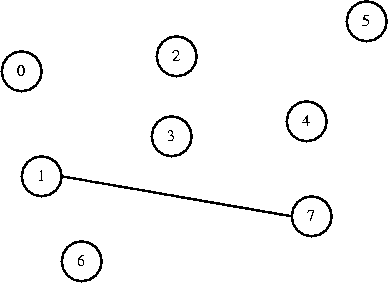
0 1 2 3 4 5 6 7
[-1] [-1] [-1] [-1] [-1] [-1] [-1] [ 1]
The parent of 7 is now 1, and 7 is no longer the root of the tree. If we
want to find 7's parent, we simply look at its value, which is 1. To find
1's parent, we look at its value, which is -1, indicating that 1 has no
parent and is the root of the tree.
Now I decide to connect 2 to 1. They are in different sets, so I connect them.
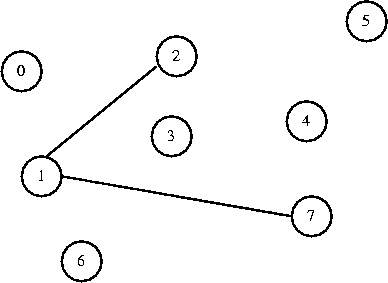
0 1 2 3 4 5 6 7
[-1] [-1] [ 1] [-1] [-1] [-1] [-1] [ 1]
Now I decide to connect 0 to 7. They are in different sets, so I connect them.
Notice that I attach them at the root, rather than root to leaf. This makes
the tree broader, whcih speeds up the find operation when it comes time to
traverse.
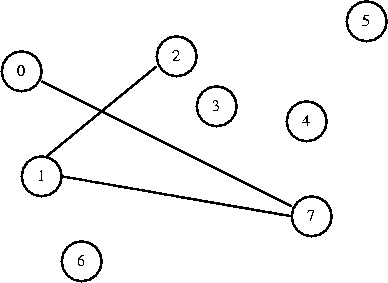
0 1 2 3 4 5 6 7
[ 1] [-1] [ 1] [-1] [-1] [-1] [-1] [ 1]
I want to connect 4 to 6. They are in different sets, so I connect them.
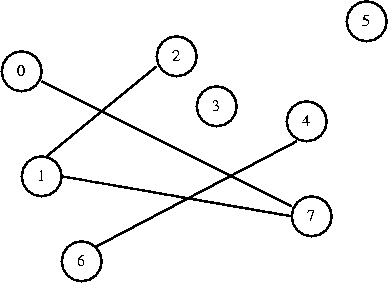
0 1 2 3 4 5 6 7
[ 7] [-1] [ 1] [-1] [ 6] [-1] [-1] [ 1]
I want to connect 5 to 6. They are in different sets, so I connect them.
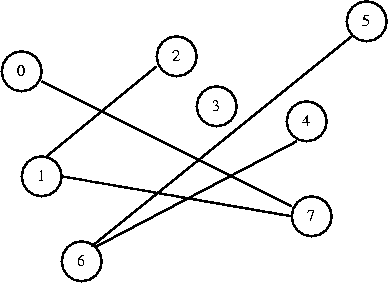
0 1 2 3 4 5 6 7
[ 7] [-1] [ 1] [-1] [ 6] [ 6] [-1] [ 1]
Note that connect 4 to 5 would now create a cycle.
I want to connect 1 to 4. They are in different sets, so I connect them.
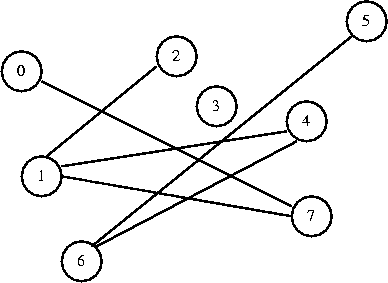
0 1 2 3 4 5 6 7
[ 7] [ 6] [ 1] [-1] [ 6] [ 6] [-1] [ 1]
How do you find out what set a particular vertex of the graph belongs to?
You simply follow its ancestors up until you find an array element with a
value of -1. At this point, all vertices except 3 are in the same set
-- 6. 6 is the only element with a value of -1. Vertex 6 is the root of
the tree consisting of all of the vertices in the graph.
The operation that connects to vertices by changing the array element
value of one to be the other is called union. The operation that
finds the root of a particular vertex's tree is called find.











