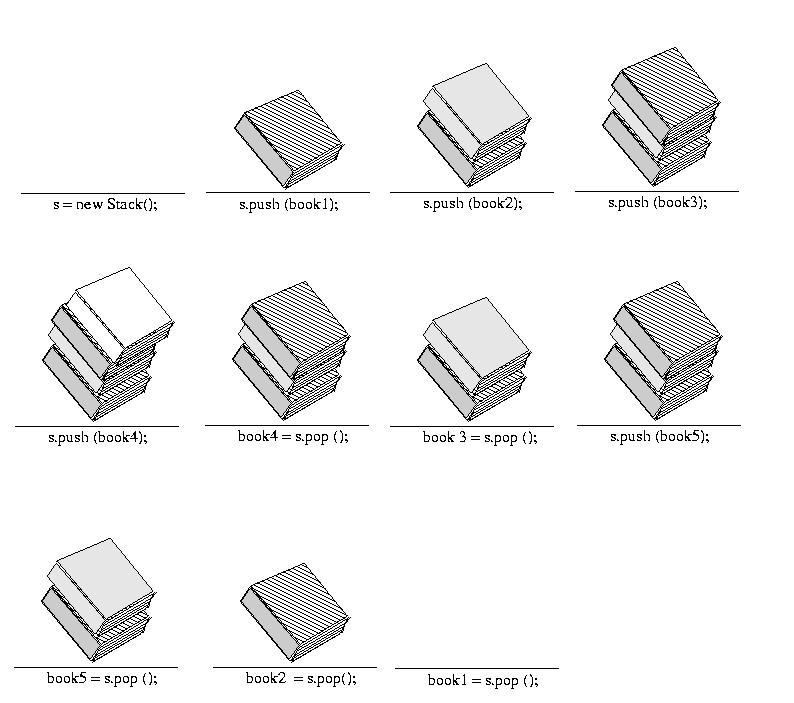
Stacks
In the real world, a stack is a way of organizing something where all of the items are piled on top of one another. We might have a stack of papers on a desk, a stack of books, etc. The easiest way to work with the items that are in the stack is to take off the one on the top and process it. The easiest way to add something to the stack is to put it on the top of the pile.
In computer science, we can implement a stack in a similar way. A stack is a first-in-last-out data structure where we always remove the item which has most recently been added to the stack. This means that in order to remove the first item that we added we first have to remove everything else, which is why we say that it is a first-in-last-out structure.
Let's look at the operations on a stack:
Consider the example of a "book stack" shown below:

Why Use Stacks?
Stacks are far less powerful than arrays or ArrayLists. We don't use them because we want more power -- we use them because we want more discipline. We'll talk about many examples of their use, beginning next class.But for now, let me mention some things that might, or might not, be familiar to you. If not, don't fret -- we'll get there. Sometimes we use stacks to store the intermediate steps in a calculation. Consider, for example, RPN calculators, like the famous HP scientific calculators.
Or, perhaps most familiar at all is the "undo stack" used by popular software to allow you to undo actions. Each time you make a change, it pushes it onto the stack. That way, you can choose to "undo", which will pop the stack to figure out what you did and then undo it. By using a stack, instead of a random-access or sequentially accessed collection of changes, we ensure that the user is offered a choice of prior versions of the document, in an understandable one-at-a-time way. Without this, the "undo" option would really degenerate into an unorganized menu of the opposites of popular options, right? Think about it -- here are the opposites of a bunch of things you did recently, would you care to select one? That would be an odd feature, indeed!
Stacks and Postfix Expressions
To help you to gain a clear understanding of how stacks work, we'll apply stacks to the pursuit of evaluating arithmetic expressions.I'm sure that the following expression looks familiar to you.
2 + 2
The style used to write this expression (two, then plus, then two) is called infix notation, and it's the style most commonly seen in arithmetic. But there are other ways of writing arithmetic expressions.
You probably know that the 2's are operands, and that the + is the operator associated with the operands. The plus operates on the 2's. Infix notation order is "operand operator operand" for all binary operators (e.g., + - * /).
But have you ever seen the same expression written this way?
2 2 +
maybe on a calculator display?
This is called postfix notation, because the operator comes after its operands.
Postfix Notation
When expressions get more complicated, parentheses come into play. For instance, take the expression
(3 + 6) * (2 - 4) + 7.
Remember the order of operations that you learned as a child in arithmetic?
You evaluate 3+6 and 2-4 first. After you get 9 and -2, respectively, you multiply those together to get -18. Finally, by adding 7, you achieve a final result of -11. Postfix notation, on the other hand, looks like this:
2 4 +.
Now, instead of having "operand operator operand", you have "operand operand operator".
The "post" in postfix means that the operator comes after its operand(s).
Look at the infix expression.
(4 + 5) * 3 - 7
A quick infix evaluation will lead you to a result of 20.
In postfix notation, this expression would be
4 5 + 3 * 7 -
You know how to evaluate an infix expression, probably in your sleep. But do you know how to evaluate that same expression if it's in postfix notation? Here's how.
Work through the postfix expression from left to right. Every time you encounter an operator, evaluate the two operands that came before it. Save the result of the operation on the two operands, and continue until you have evaluated the entire expression.
What's so great about postfix notation? As you can see, it eliminates all parentheses. Postfix notation is used in some applications because it saves on memory. After a few times of looking at postfix notation, it becomes easier to read.
So how do you convert an infix expression to a postfix expression?
Converting from Infix Notation to Postfix Notation by Hand
Converting an expression from infix to postfix is easy.
The first thing you need to do is fully parenthesize the expression.
So, the expression
(3 + 6) * (2 - 4) + 7
becomes
(((3 + 6) * (2 - 4)) + 7).
Now, move each of the operators immediately to the right of their respective right parentheses.
If you do this, you will see that
(((3 + 6) * (2 - 4)) + 7)
becomes
3 6 + 2 4 - * 7 +
Take a close look at the arrowheads. To convert an infix expression to postfix, you simply place each operator in the infix expression immediately to the right of its respective right parenthesis. Then you rewrite the expression in the new order, and what you get is the same expression in prefix notation.
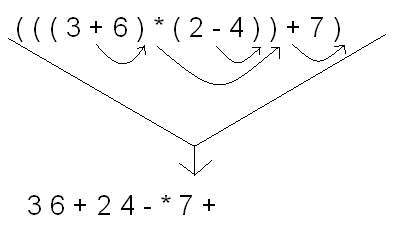
Try converting some infix expressions of your own into prefix notation. As you can see, it's easy to do.
Evaluating Postfix Notation With a Stack
One beautiful thing about postfix notation is that it is easily implemented in programming by using a stack. Here's how to do it.Read in one symbol at a time from the postfix expression.
Any time you see an operand, push it onto the stack. Any time you see a binary operator (+, -, *, /) or unary (square root, negative sign) operator ,
- If the operator is binary, pop two elements off of the stack.
- If the operator is unary, pop one element off the stack.
- Evaluate those operands with that operator
- Push the result back onto the stack.
When you're done with the entire expression, the only thing left on the stack should be the final result. If there are zero or more than 1 operands left on the stack, either your program is flawed, or the expression was invalid.
Very Important:
The first element you pop off of the stack in an operation should be evaluated on the right-hand side of the operator. For multiplication and addition, order doesn't matter, but for subtraction and division, your answer will be incorrect if you switch your operands around.Step through this example. By the end of it, it will be clear to you how a stack can easily evaluate a postfix expression. Here, we use a stack to evaluate the expression 4 5 + 9 * 3 + 3 /.