Insertion Sort

Insertion sort works, as before, by viewing the list as two sub-lists, one of unsorted items, initially full, and one of unsorted items, initially empty. As before, each iteration, the next item from the unsorted list enters the sorted list.

Bascially, we remove the next item from the unsorted list, and that gives us an extra slot in the sorted list. We then move each item, one at a time, into that slot, until we make a "hole" in the right place to insert the new item. When we do, we place it there.

Much like Bubble sort and Selection sort, Insertion sort is still requires a multiple of N² operations. We move one item to the sorted list each time, so we need to make n passes. And then, each pass, we need to compare it to n/2 items (amortized over all runs).

It is however, quite a bit more expensive in real time. Displacing an item in an array is quite expensive -- everything after it needs to be copied.

But, what is special about insertion sort is that it can be started before all of the data arrives. New data can still be sorted, even if it is lower (or higher) than those already fixed in place.

Also, the cost of displacing an item isn't present, if a Linked List is being sorted.

Here's an example:

4	7	9	2	5	8	1	3	6
4	7	9	2	5	8	1	3	6
4	7	9	2	5	8	1	3	6
4	7	9	2	5	8	1	3	6
4	7	9	2	5	8	1	3	6
2	4	7	9	5	8	1	3	6
2	4	7	9	5	8	1	3	6
2	4	5	7	9	8	1	3	6
2	4	5	7	9	8	1	3	6
2	4	5	7	8	9	1	3	6
2	4	5	7	8	9	1	3	6
1	2	4	5	7	8	9	3	6
1	2	4	5	7	8	9	3	6
1	2	3	4	5	7	8	9	6
1	2	3	4	5	7	8	9	6
1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9

Insertion Sort Code

 public void insertionSort(int[] numbers)
  {
    /*going through all of the items in the array*/
    for (int insertMe=1; insertMe < numbers.length; insertMe++)
    {
      /*find the correct index for the item*/
      for (int newPosn=0; newPosn < insertMe; newPosn++)
      {
        /*stop when you come to an item greater than the item in question*/
        if (numbers[insertMe] < numbers[newPosn])
        {
          /*put the item in question somewhere for safe keeping*/
          int temp = numbers[insertMe];
          
          /*move everything after the correct index down to make room*/
          for (int shift=insertMe; shift > newPosn; )
            numbers[shift] = numbers[--shift];

          /*put the item in its correct index*/
          numbers[newPosn] = temp;

          /*You've found the right index for the item and it's time to stop*/
          break;
        }
      }
    }
  }

A Quick Look at the Cost of Sequential Searching

So, if, in performing a linear search, we get lucky, we'll find what we are looking for on the first try -- we'll only have to look at one item. But, if we get unlucky, it'll be the last item that we consider, and we'll have had to look at each and every item. In the average case, we'll look at about half of the items.

The "Binary" Search

But, let's consider a different case for a moment. The case of a sorted, indexed list. Let's consider, for example, looking for a particular number in a sorted list of numbers stored within an array or Vector:

Numbers:	3	7	8	9	11	14	19	25	31	32
Index:	0	1	2	3	4	5	6	7	8	9

We know that this list is in order. So, we know that there is just as good a chance that it comes before the "middle" as it does after the "middle". In other words, whatever number we are looking for is just as likely to be in the list of numbers with indexes 0-4 as it is the list with indexes 5-9.

So, we can compare the number with one of the two "middle" numbers, the number at index 4 or the number at index 5. If it happens to be the one we're looking for, we got lucky -- and can celebrate.

If not, we'll know better where to look. If it is less than this "middle" number, it has an index less than the middle number. If it has an index greater than the middle number, it has an index greater than the middle number. Either way, we've eliminated half of the possible places to search. We can search must faster by considering only those numbers in the right half of the list.

Since this approach decides between searching two sublists, it is often known as a binary search. Binary means having two states -- in this case, left and right (a.k.a, less than and greater than).

To better illustrate this, I'll pseudocode this algorithm recursively, and then go through it by hand. The recursive algorithm looks like this:

  public static void searchSortedIntArray (int findMe, int []list, int beginIndex, int endIndex)
  {
    int middleIndex = beginIndex + (endIndex - beginIndex)/2;

    // If the middle point matches, we've won
    if (list[middleIndex] == findMe)
      return true;

    // If it is in the left list, and the left list is non-empty, look there.
    if ( (list[middleIndex] > findMe) && (middleIndex > beginIndex) )
      return searchSortedIntArray (findMe, list, beginIndex, middleIndex-1 );

    // If it is in the right list and the right list is non-empty, look there.
    if ( (list[middleIndex] < findMe) && (middleIndex < endIndex) )
      return searchSortedIntArray (findMe, list, middleIndex+1, endIndex);

    // We're not it and the correct sub-list is empty -- return false
    return false;
  }
  

Now, to go through it by hand, let's first pick a number in the list: 8. We start out looking at index (9/2)=4, which contains 11. Since 7 is less than 11, we consider the sublist with indexes 0-3. Since (3/2)=1, we next consider 7, the valuse at index 1. Since 7 is less than 8, we look at its right sublist: beginning with index 2 and ending with index 3. The next "middle" index is 2+(3/2)=3. Index 3 contains 8, so we return true. As things unwind, that propagates to the top.

Now, let's pick a number that is not in the list: 26. Again, we start with the vlaue 11 at index 4 -- this time we go next to the right sublist with indexes 5 through 9. The new pivot point is 7. The value at this point is 25. Since 26 is greater than 25, we consider the right sublist with indexes 8 and 9. The new pivot is index 8, which holds the value 31. Since 26 is less than 31, we want to look at the left sublist, but we can't, it is empty. Index 26 is both the middle point, and the left point. So, we return false, and this is propogated through the unwinding -- 26 is not in the list.

A Careful Look at the Cost of Binary Search

Each time we make a decision, we are able to divide the list in half. So, we divide the list in half, and half again, and again, until there is only 1 thing left. Discounting the "off by one" that results from taking the "pivot" middle value out, we're dividing the list exactly in half each time and searchong only one half.

As a result, in the worst case, we'll have to search Log₂ N items. Remember 2^X = N. So, for a list of 8 items, we'll need to consider approximately 3 of them. Take a look at the table below, and trace through a list by hand to convince yourself:

N	Max. Attempts
1	1=(0+1); 20=1
2	2=(1+1); 21=2
3	2=(1+1); 21=2
4	3=(2+1); 22=4
5	3=(2+1); 22=4
6	3=(2+1); 22=4
7	3=(2+1); 22=4
8	3=(2+1); 22=4
9	4=(3+1); 23=8
9	4=(3+1); 23=8
10	4=(3+1); 23=8
11	4=(3+1); 23=8
12	4=(3+1); 23=8
13	4=(3+1); 23=8
14	4=(3+1); 23=8
15	4=(3+1); 23=8
16	5=(4+1); 24=16

And, as before, the average number of attempts will be half of the maximum number of attempts, as shown in the plots below:

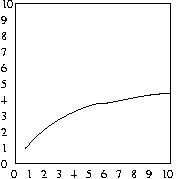
Worst case of binary search

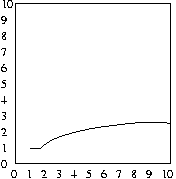
Average case of binary search

Thinking About The Cost of Operations Upon Indexed Data Structures

Indexed Data Structures are a means of storing information in a manner that enables us to retrieve the data by calling on its index. In an abstract sense it does not matter if it is an array, an ArrayList or a Vector. They are all rich data structures but when you take two steps back and look at them, then you basically have an array. They are all indexes structures. This means instant acess to an item in the array by address. Accessing data by address is known as random access. There is no penalty(or cost) for jumping around in the data structure. There is also sequencial access, we can look at things either forwards or backwards in order.

So indexed data structures offer instant random access and sequential access

What is the cost of jumping right to something in this array? We do not know exactly so we will make it C. The cost is the same no matter what we are accessing, therefore C is a constant. If we want to travel through this array forwards or backwards, the cost is C for each element and if there are 10 elements in the array the cost is 10c, if there are n elements then the cost is n*C.

Getting something by index is what we call a constant time index. No matter how long the array is the cost of getting to the third element is always the same. The total cost of a traversal is directly proportional to the number of elements in the array.

Knowing the cost helps us then understand other elements of the data structures. If this array is completely out of order then finding something inside of the structure will cost n*C -> worst case scenario. If I get lucky I could take my first step and find it. I am not lucky so I would walk through the whole array and it wont be there. The cost of that will be n*C because I had to walk through each element of the array to get to the end.

• Best case: C
• worst case: n*C,
• average: 1/2n*C

Since I have no idea what C is, I am just going to factor out the C and call it 1. The Big-O of 1, O(1) is constant time. Big-O notation is an apporoximate notation. It is there to capture the shape of the curve, the big picture and that's the main reason why I can throw out the C. Mathematicians may cringe, but for computer programmers constants like 2, 10, and C are all the same and we don't care about them when it comes to Big-O notation.

• O(1)is constant time,
• O(n) is linear time.

As time varies the curve changes. In this notation I have thrown out the constant and I have thrown out the lesser terms. If it was (n+2) I would have thrown out the +2.

Do you remember end behavior? If you took a look at x², everything that has x² as the largest term has the same basic shape. Big-O is concerned with the large basic shape. It is concerned with the large big picture, the end behavior.

Say we had 3n³+ 9n²+ 1/2n +2000000

The 2000000 may be significant for smaller data sets, but if I have enough items to amortize it against then it stops mattering. If we square one million, compared to the first term, two million is negligible. It is the 3n³ that is going to control the end behavior. If you remember from high school algebra class, we dont care about the 3 the coefficient, because eventually the n³ term will be significantly bigger at the end behavior, no matter what. In the end all that will matter is the n³.

So in introducing Big-O notation, I am talking about worst case scenario behavior and end behavior.

• The traversal is O(n).
• A search is a type of traversal so it is O(n).

But what about an insertion, what if I want to insert something in the middle and push everything else back a space? Now what is the cost going to be?

If I have n items then the detailed cost is ((n-1)-x), but the Big-O of the cost is O(n). X and -1 are constants and they get thrown away. If we take two steps backwards, we know that if we have to insert in the first slot 0 then we will have to shift n things, so Big-O = O(n).

We know from programming that this shift is a variable assignment and all the variable assignments are roughly the same cost, so O(n) makes sense.

What if I flip this problem around, and I want to remove an item from this list? From first principals would be ((n-1)-x) so the Big-O is O(n). Then intuition tells us that in the worst case I am removing the 0th element, therefore I am moving all the other terms and it is still the same variable assignment operation. So for this removal the Big-O is still O(n).

So we see that:

• random access is O(1)
• traversal is O(n)
• insert is O(n)
• removal is O(n)

Generally speaking when we are talking about Big-O we are talking about time. The old thinking was that storage could be bought but, processor speed is hard to come by. Therefore the Big-O usually refers to time unless specified for space.

Sorts and Big-O

Bubble Sort

A bubble sort traverses the array, or a selected portion of the array, length-1 times (a less efficient version of the bubble sort could pass through the array length times and still produce a sorted array). With each pass through the array, the bubble sort compares adjacent values, swapping them if necessary. This actually results in "bubbling" the highest value in the array up to the highest index (length-1) by the end of the first pass through the array, the second-highest value up to the second-highest index (length-2) after the second pass through the array, and so on. By the time the bubble sort has made length-1 passes through the array (or a selected portion of the array), every item, including the lowest item, is guaranteed to be in its proper place in the array. What is the runtime for this sort?

Let's say we have 10 numbers. The outer for loop of the bubble sort has to run 9 times (once when last_one = 9, once when it = 8, etc., up until it = 1, and when it hits 0 it stops). If we had 100 numbers, the outer loop would run 99 times. If we had 1000 numbers, the outer loop would run 999 times. In general, if there are N numbers, the outer loop will run (N-1) times, but to simplify our math we will say that it runs N times.

If the outer loop runs N times, then the total running time is N times the amount of work done in one iteration of the loop. So how much work is done in one iteration? Well, one iteration of the outer for loop includes one complete running of the inner for loop. The first time through, the inner loop goes 9 times, the second time through it goes 8 times, then 7, and so on. On average, the inner loop goes N/2 times, so the total time is N for the outer loop times N/2 for the inner loop times the amount of work done in one iteration of the inner loop.

For one iteration of the inner loop, we either do nothing if the number in the less than the one after it, or we set three values if we need to swap. In the worst case, we will need to swap at every step, so we will say that the one iteration of the inner loop requires 3 operations. That makes the total time for the bubble sort algorithm N*(N/2)*3 operations, or (3/2)*N²

Selection Sort

In the selection sort, we find the smallest value in the array and move it to the first index, then we find the next-smallest value and move it to the second index, and so on. We start at the first index and walk through the entire list, keeping track of where we saw the lowest value. If the lowest value is not currently at the first index, we swap it with the lowest value. What is the runtime for this sort?

Selection sort slightly better than the bubble sort, because we swap at most once for every index, instead of potentially once for each item. We find the correct index for that particular number. Then we swap it into its correct place in the array.

But the Big-O is exactly the same: O(n²). Each pass through the list, we fix the position of only one more item, so we still need to make n passes. And, each pass, we must compare ourselves to, n/2 other items (amortized cost, since the list shrinks from n to 1). As before, this leaves us with 1/2*n², but we drop the coefficient and focus on the outer-bound behavior for Big-O.

Insertion Sort

Insertion sort works, as before, by viewing the list as two sub-lists, one of unsorted items, initially full, and one of unsorted items, initially empty. As before, each iteration, the next item from the unsorted list enters the sorted list.

Bascially, we remove the next item from the unsorted list, and that gives us an extra slot in the sorted list. We then move each item, one at a time, into that slot, until we make a "hole" in the right place to insert the new item. When we do, we place it there.

Much like Bubble sort and Selection sort, Insertion sort is O(n²). We move one item to the sorted list each time, so we need to make n passes. And then, each pass, we need to compare it to n/2 items (amortized over all runs). So, it requires 1/2*n*n operations for a Big-O of O(n²).

It is however, quite a bit more expensive in real time. Displacing an item in an array is quite expensive -- everything after it needs to be copied. But, what is special about insertion sort is that it can be started before all of the data arrives. New data can still be sorted, even if it is lower (or higher) than those already fixed in place. Also, the cost of displacing an item isn't present, if a Linked List is being sorted.

Searching and Big-O

The "Sequential Search", a.k.a., The "Brute Force Search" and The "Linear Search"

One approach to search for something is just to consider each item, one at a time, until it is found -- or there are no more items to search. I remember using this approach quite a bit as a child. I'd open my toy box and throw each toy out, until I found the one I was looking for. (Unfortunately, this approach normally resulted in a parental command to clean my room -- and someitmes quite a fuss).

Imagine that I had a toybox containing 10 items. In the average case, I'd end up throwing 4 or 5 items on the floor, and my treasured toy would be the 5th or 6th item -- I'd have to search half of the toy box. Sometimes, I would find it the first time -- right on top. Sometimes it'd be the last one -- at the very bottom. And on the balance of occasions -- somewhere in between.

Binary Search: No Silver Bullet

So, instead of searching in O(n) time using a linear search, we can search in O(log n) time, usng a bianry search -- that's a huge win. But, there is a big catch -- how do we get the list in sorted order?

We can do this with a quadratic sort, such as Bubble sort, Selection Sort, or Insertion Sort, in which case the sort takes O(n²) time. Or, we can use Quick Sort, in which case, if we are not unlucky, it'll take "n*log n" time. And, soon, we'll learn about another technique that will let us reliably sort in O(n*log n) time. But, none of these options are particularly attractive.

If we are frequently inserting into our list, and have no real reason to keep it sorted, except to search, our search really degenerates to O(n*log n) -- becuase we are sorting just to search. And, O(n*log n) is worse than the O(n) "brute force" search.