An Introduction to Sorts

You probably did at least a small amount of sorting in your introductory course. Sorting a collection of items is an important computing application. There are many commonly-used sorting algorithms. Some of them are good for sorting small sets of data, while others are good for sorting large sets of data. Some are good under certain conditions and horrid in other conditions. Some take about the same length of time to run no matter what the conditions. Some are simple, others are a bit more complicated.

In order to keep things simple and focus our attention on sorting, we'll sort an array of integers, from lowest to highest, in our examples. In reality, you can sort any collection of Objects (remember Comparable).

Bubble Sort

A bubble sort traverses the array, or a selected portion of the array, length-1 times (a less efficient version of the bubble sort could pass through the array length times and still produce a sorted array). With each pass through the array, the bubble sort compares adjacent values, swapping them if necessary. This actually results in "bubbling" the highest value in the array up to the highest index (length-1) by the end of the first pass through the array, the second-highest value up to the second-highest index (length-2) after the second pass through the array, and so on. By the time the bubble sort has made length-1 passes through the array (or a selected portion of the array), every item, including the lowest item, is guaranteed to be in its proper place in the array.

Let's see how the bubble sort works on an array of integers. We start at the lowest pair of indexes, and work our way up to the highest.

The following shows one entire pass through the array using a bubble sort. Turn your head sideways to the left to read this array. The array indexes are the left-hand, red column. The two adjacent items currently being compared are bold. Note that there are eight total items in the array. Notice that we will make seven comparisons (there are eight columns after the red column) during this first pass.

7		7		7		7		7		7		7		7		9
6		4		4		4		4		4		4		9		7
5		5		5		5		5		5		9		4		4
4		6		6		6		6		9		5		5		5
3		3		3		3		9		6		6		6		6
2		1		1		9		3		3		3		3		3
1		2		9		1		1		1		1		1		1
0		9		2		2		2		2		2		2		2

What has happened to the 9 that started at index 0? It happened to be the highest value in the array, so every time we compared adjacent values we had to swap until the 9 was finally in the last position in the array. After one pass through the array, we have successfully moved the highest value into the highest index.

On our next pass through the array, we'll move the second-highest value into the second-highest index. This time we will stop at the second-to-last pair of values, since we already know that the highest value is at the highest index. The 9 is in blue, since it is already at its proper index.

7		9		9		9		9		9		9		9
6		7		7		7		7		7		7		7
5		4		4		4		4		4		6		6
4		5		5		5		5		6		4		4
3		6		6		6		6		5		5		5
2		3		3		3		3		3		3		3
1		1		2		2		2		2		2		2
0		2		1		1		1		1		1		1

On the second pass through, the second-highest value was already in the second-highest position in the array, but we did move some of the other values one step closer to being in the correct position. Notice that this time, we made only six comparisons (see that there are only seven columns after the red column). There's no need to make the seventh comparison, since the 9 is already in its proper place. 

We continue this process until we have moved every value to the correct index.

Bubble Sort Code

public void bubbleSort(int[] numbers)
{
     /*traverse the array (or a subset of the array) length-1 times*/
     for (int highest_unsorted=numbers.length-1; highest_unsorted != 0; highest_unsorted--)
     {    
        /*makes the necessary comparisons for one pass through the array*/      
        for (int best_so_far=0; best_so_far < highest_unsorted; best_so_far++)
        {
                        /*compare adjacent items and swap them if necessary*/
                        if (numbers[best_so_far] > numbers[best_so_far+1])
                                swapNumbers (best_so_far, best_so_far+1);
        }
     }
}


public void swapNumbers(int i, int j)
{
        int temp = numbers[i];  /*put numbers[i] somewhere to keep it safe*/
        numbers[i] = numbers[j];        /*put numbers[j] at index i*/
        numbers[j] = temp;               /*put numbers[i] at index j*/
}

Now we're going to pause for a minute to introduce something called "algorithmic complexity". It basically measures how expensive an algorithm is. There are many different ways to measure cost, whether by how much money something is, how much time is spent, power, etc. Computers are often measured on what is called "runtime", essentially how much time on a stopwatch it takes to run an algorithm. This can be made much faster with more ram, a faster processor, etc. Algorithmic complexity, on the other hand, just looks at the algorithm independent of the environment it is run on, and simply answer the question, 'how complex is it?' To measure, we have to specify what case we're measuring, whether the best case, the worst case, or the average case. Usually, computer scientists concentrate on the worst case, often called an outer bound. The notation for this is O, spoken as "big O". To do this, we have to ignore many things, such as constant time factors.

Analyzing Running Time

The bubble sort is a sorting algorithm which is very easy to implement, but how good is this algorithm? In order to answer this question, we need to look at how much work the algorithm has to do. When we analyze the running time of an algorithm, we want to look at the bigger picture, so we will make some approximations and ignore constant factors in order to simplify the analysis.

Let's say we have 10 numbers. The outer for loop of the bubble sort has to run 9 times (once when last_one = 9, once when it = 8, etc., up until it = 1, and when it hits 0 it stops). If we had 100 numbers, the outer loop would run 99 times. If we had 1000 numbers, the outer loop would run 999 times. In general, if there are N numbers, the outer loop will run (N-1) times, but to simplify our math we will say that it runs N times.

If the outer loop runs N times, then the total running time is N times the amount of work done in one iteration of the loop. So how much work is done in one iteration? Well, one iteration of the outer for loop includes one complete running of the inner for loop. The first time through, the inner loop goes 9 times, the second time through it goes 8 times, then 7, and so on. On average, the inner loop goes N/2 times, so the total time is N for the outer loop times N/2 for the inner loop times the amount of work done in one iteration of the inner loop.

For one iteration of the inner loop, we either do nothing if the number in the less than the one after it, or we set three values if we need to swap. In the worst case, we will need to swap at every step, so we will say that the one iteration of the inner loop requires 3 operations. That makes the total time for the bubble sort algorithm N*(N/2)*3 operations, or (3/2)*N²

Selection Sort

Now let's look at another easy sort, called the selection sort. With Bubble sort, we remembered the "smallest value so far" by swapping it into current position of the list during each step of each iteration. Although this works, it take a lot of effort to swap numbers around -- especially if all we really need to know is the index of the "smallest value so far". This is the critical difference in thw two sorts -- Selection Sort just remembers the position fo the "best so far", instead of swapping it into the current position. This reduces the amount of work required during each step of the sort. Then, at the end of each pass, it swaps just once.

So, let's take a look at this step-by-step. In the selection sort, we find the smallest value in the array and move it to the first index, then we find the next-smallest value and move it to the second index, and so on. We start at the first index and walk through the entire list, keeping track of where we saw the lowest value. If the lowest value is not currently at the first index, we swap it with the lowest value.

Now, let's take a look at an example. We will start with the same set of numbers we used before.

0	1	2	3	4	5	6	7
9	2	1	3	6	5	4	7

So the first step in the selection sort is to get the lowest value into the lowest index (index 0 in this case). We will loop through all of the values, keeping track of which index contains the lowest value. Since we are trying to fill index 0, we will assume that the lowest value is already there unless we find one that is lower - we initialize our best index to be index 0.

As we scan through, we find that the lowest value is the 1 which is at index 2, so we swap the value at index 0 with the value at index 2.

0	1	2	3	4	5	6	7
1	2	9	3	6	5	4	7

Now the lowest value is at index 0, so the next step is to get the next-lowest value into index 1. When we scan through the numbers, we find that the next-lowest value, the 2, is already at index 1, so we do not need to swap.

If we continue through the array one index at a time, we will eventually move every value into the appropriate index, resulting in a sorted array.

Selection Sort Code

public void selectionSort(int[] numbers)
{
    /*For every index in the array, with the exception of the last one,*/
    for(int searcherIndex=0; searcherIndex < numbers.length-1; searcherIndex++)
    {
        /*Assume that the number is where it's supposed to be*/
        int correctIndex = searcherIndex;
        
        /*Try out other candidate indexes*/
        for (int candidateIndex=searcherIndex+1; candidateIndex < numbers.length; candidateIndex++)
        {
                /*If you find a smaller number, make it's index the correct index*/
                if(numbers[candidateIndex] < numbers[correctIndex])
                                correctIndex = candidateIndex;
        }
        /*At this point correctIndex really will be the correct index*/
        swapNumbers (searcherIndex, correctIndex);
    }
}

Running Time of Selection Sort

Selection sort slightly better than the bubble sort, because we swap at most once for every index, instead of potentially once for each item. We find the correct index for that particular number. Then we swap it into its correct place in the array.

Insertion Sort

Insertion sort works, as before, by viewing the list as two sub-lists, one of unsorted items, initially full, and one of unsorted items, initially empty. As before, each iteration, the next item from the unsorted list enters the sorted list.

Bascially, we remove the next item from the unsorted list, and that gives us an extra slot in the sorted list. We then move each item, one at a time, into that slot, until we make a "hole" in the right place to insert the new item. When we do, we place it there.

Much like Bubble sort and Selection sort, Insertion sort is still requires a multiple of N² operations. We move one item to the sorted list each time, so we need to make n passes. And then, each pass, we need to compare it to n/2 items (amortized over all runs).

It is however, quite a bit more expensive in real time. Displacing an item in an array is quite expensive -- everything after it needs to be copied.

But, what is special about insertion sort is that it can be started before all of the data arrives. New data can still be sorted, even if it is lower (or higher) than those already fixed in place.

Also, the cost of displacing an item isn't present, if a Linked List is being sorted.

Here's an example:

4	7	9	2	5	8	1	3	6
4	7	9	2	5	8	1	3	6
4	7	9	2	5	8	1	3	6
4	7	9	2	5	8	1	3	6
4	7	9	2	5	8	1	3	6
2	4	7	9	5	8	1	3	6
2	4	7	9	5	8	1	3	6
2	4	5	7	9	8	1	3	6
2	4	5	7	9	8	1	3	6
2	4	5	7	8	9	1	3	6
2	4	5	7	8	9	1	3	6
1	2	4	5	7	8	9	3	6
1	2	4	5	7	8	9	3	6
1	2	3	4	5	7	8	9	6
1	2	3	4	5	7	8	9	6
1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9

Insertion Sort Code

 public void insertionSort(int[] numbers)
  {
    /*going through all of the items in the array*/
    for (int insertMe=1; insertMe < numbers.length; insertMe++)
    {
      /*find the correct index for the item*/
      for (int newPosn=0; newPosn < insertMe; newPosn++)
      {
        /*stop when you come to an item greater than the item in question*/
        if (numbers[insertMe] < numbers[newPosn])
        {
          /*put the item in question somewhere for safe keeping*/
          int temp = numbers[insertMe];
          
          /*move everything after the correct index down to make room*/
          for (int shift=insertMe; shift > newPosn; )
            numbers[shift] = numbers[--shift];

          /*put the item in its correct index*/
          numbers[newPosn] = temp;

          /*You've found the right index for the item and it's time to stop*/
          break;
        }
      }
    }
  }

The "Sequential Search", a.k.a., The "Brute Force Search" and The "Linear Search"

One approach to search for something is just to consider each item, one at a time, until it is found -- or there are no more items to search. I remember using this approach quite a bit as a child. I'd open my toy box and throw each toy out, until I found the one I was looking for. (Unfortunately, this approach normally resulted in a parental command to clean my room -- and someitmes quite a fuss).

Imagine that I had a toybox containing 10 items. In the average case, I'd end up throwing 4 or 5 items on the floor, and my treasured toy would be the 5th or 6th item -- I'd have to search half of the toy box. Sometimes, I would find it the first time -- right on top. Sometimes it'd be the last one -- at the very bottom. And on the balance of occasions -- somewhere in between.

A Quick Look at the Cost of Sequential Searching

So, if, in performing a linear search, we get lucky, we'll find what we are looking for on the first try -- we'll only have to look at one item. But, if we get unlucky, it'll be the last item that we consider, and we'll have had to look at each and every item. In the average case, we'll look at about half of the items.

Since, the worst case could require looking at each and every item, it is really easy to see that this seach is O(n). And, the average case is also linear time -- so, unlike quck sort, this is rough going in most cases.

The "Binary" Search

But, let's consider a different case for a moment. The case of a sorted, indexed list. Let's consider, for example, looking for a particular number in a sorted list of numbers stored within an array or Vector:

Numbers:	3	7	8	9	11	14	19	25	31	32
Index:	0	1	2	3	4	5	6	7	8	9

We know that this list is in order. So, we know that there is just as good a chance that it comes before the "middle" as it does after the "middle". In other words, whatever number we are looking for is just as likely to be in the list of numbers with indexes 0-4 as it is the list with indexes 5-9.

So, we can compare the number with one of the two "middle" numbers, the number at index 4 or the number at index 5. If it happens to be the one we're looking for, we got lucky -- and can celebrate.

If not, we'll know better where to look. If it is less than this "middle" number, it has an index less than the middle number. If it has an index greater than the middle number, it has an index greater than the middle number. Either way, we've eliminated half of the possible places to search. We can search must faster by considering only those numbers in the right half of the list.

Since this approach decides between searching two sublists, it is often known as a binary search. Binary means having two states -- in this case, left and right (a.k.a, less than and greater than).

To better illustrate this, I'll pseudocode this algorithm recursively, and then go through it by hand. The recursive algorithm looks like this:

  public static void searchSortedIntArray (int findMe, int []list, int beginIndex, int endIndex)
  {
    int middleIndex = beginIndex + (endIndex - beginIndex)/2;

    // If the middle point matches, we've won
    if (list[middleIndex] == findMe)
      return true;

    // If it is in the left list, and the left list is non-empty, look there.
    if ( (list[middleIndex] > findMe) && (middleIndex > beginIndex) )
      return searchSortedIntArray (findMe, list, beginIndex, middleIndex-1 );

    // If it is in the right list and the right list is non-empty, look there.
    if ( (list[middleIndex] < findMe) && (middleIndex < endIndex) )
      return searchSortedIntArray (findMe, list, middleIndex+1, endIndex);

    // We're not it and the correct sub-list is empty -- return false
    return false;
  }
  

Now, to go through it by hand, let's first pick a number in the list: 8. We start out looking at index (9/2)=4, which contains 11. Since 7 is less than 11, we consider the sublist with indexes 0-3. Since (3/2)=1, we next consider 7, the valuse at index 1. Since 7 is less than 8, we look at its right sublist: beginning with index 2 and ending with index 3. The next "middle" index is 2+(3/2)=3. Index 3 contains 8, so we return true. As things unwind, that propagates to the top.

Now, let's pick a number that is not in the list: 26. Again, we start with the vlaue 11 at index 4 -- this time we go next to the right sublist with indexes 5 through 9. The new pivot point is 7. The value at this point is 25. Since 26 is greater than 25, we consider the right sublist with indexes 8 and 9. The new pivot is index 8, which holds the value 31. Since 26 is less than 31, we want to look at the left sublist, but we can't, it is empty. Index 26 is both the middle point, and the left point. So, we return false, and this is propogated through the unwinding -- 26 is not in the list.

A Careful Look at the Cost of Binary Search

Each time we make a decision, we are able to divide the list in half. So, we divide the list in half, and half again, and again, until there is only 1 thing left. Discounting the "off by one" that results from taking the "pivot" middle value out, we're dividing the list exactly in half each time and searchong only one half.

As a result, in the worst case, we'll have to search Log₂ N items. Remember 2^X = N. So, for a list of 8 items, we'll need to consider approximately 3 of them. Take a look at the table below, and trace through a list by hand to convince yourself:

N	Max. Attempts
1	1=(0+1); 20=1
2	2=(1+1); 21=2
3	2=(1+1); 21=2
4	3=(2+1); 22=4
5	3=(2+1); 22=4
6	3=(2+1); 22=4
7	3=(2+1); 22=4
8	3=(2+1); 22=4
9	4=(3+1); 23=8
9	4=(3+1); 23=8
10	4=(3+1); 23=8
11	4=(3+1); 23=8
12	4=(3+1); 23=8
13	4=(3+1); 23=8
14	4=(3+1); 23=8
15	4=(3+1); 23=8
16	5=(4+1); 24=16

And, as before, the average number of attempts will be half of the maximum number of attempts, as shown in the plots below:

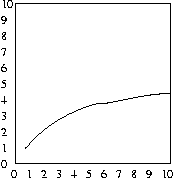
Worst case of binary search

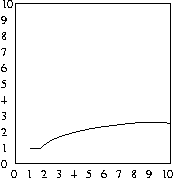
Average case of binary search

Binary Search: No Silver Bullet

So, instead of searching in O(n) time using a linear search, we can search in O(log n) time, usng a bianry search -- that's a huge win. But, there is a big catch -- how do we get the list in sorted order?

We can do this with a quadratic sort, such as Bubble sort, Selection Sort, or Insertion Sort, in which case the sort takes O(n²) time. Or, we can use Quick Sort, in which case, if we are not unlucky, it'll take "n*log n" time. And, soon, we'll learn about another technique that will let us reliably sort in O(n*log n) time. But, none of these options are particularly attractive.

If we are frequently inserting into our list, and have no real reason to keep it sorted, except to search, our search really degenerates to O(n*log n) -- becuase we are sorting just to search. And, O(n*log n) is worse than the O(n) "brute force" search.