Prim's grows the tree in successive stages. You start by choosing one vertex to be the root v, and add an edge (piece of sidewalk), and thus an associated vertex (a point of interest in the park), to the tree. At each stage, you add a vertex to the tree by choosing the vertex u such that the cost of getting from v to u is the smallest possible cost (in the case of the park, the cost is distance). At each stage, you say, "Where can I get from here?" and go down the shortest road possible from where you are.
Applying this algorithm until all vertices of the given graph are in the tree creates a minimum spanning tree of that graph. This may sound familiar. Prim's algorithm is essentially the same as Dijkstra's -- with a different cost function. They both proceed using the same greedy strategy.
Prim's finds the minimum spanning tree of the entire graph from s, so we use the Length field to record the cost of getting from a vertex v to its parent in the minimum spanning tree we're making.
Suppose we have the following graph:
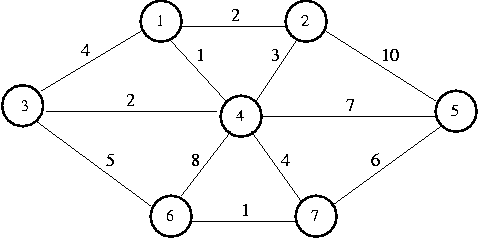
We would build a table as follows:
| Known | Path | Length | |
| 1 | - | - | INF |
| 2 | - | - | INF |
| 3 | - | - | INF |
| 4 | - | - | INF |
| 5 | - | - | INF |
| 6 | - | - | INF |
| 7 | - | - | INF |
Selecting vertex 1 and making it the root of our tree, we update its neighbors, 1, 2, 3, and 4. Vertex 1's cheapest place in the tree is known.
| Known | Path | Length | |
| 1 | Y | 1 | 0 |
| 2 | - | 1 | 2 |
| 3 | - | 1 | 4 |
| 4 | - | 1 | 1 |
| 5 | - | - | INF |
| 6 | - | - | INF |
| 7 | - | - | INF |
Next we select vertex 4 (one of the neighbors of vertex 1). It's cheapest place in the tree is now known. Every vertex in the graph is adjacent to 4.
Vertex 1 is known (meaning that its in its optimal place in the tree), so we don't examine it. We don't change vertex 2, because its Length is 2, and the edge cost from 4 to 2 is 3. We update the rest.
| Known | Path | Length | |
| 1 | Y | 1 | 0 |
| 2 | - | 1 | 2 |
| 3 | - | 4 | 2 |
| 4 | Y | 1 | 1 |
| 5 | - | 4 | 7 |
| 6 | - | 4 | 8 |
| 7 | - | 4 | 4 |
Next we select vertex 2 (another neighbor of 1) and make it known. We can't improve our tree in any way by going through vertex 2. We select vertex 3 (the last neighbor of 1) and make it known. The path from 3 to 6 is cheaper than the path from 4 to 6, so we update 6's fields.
2 and 3's cheapest places in the tree are now known.
| Known | Path | Length | |
| 1 | Y | 1 | 0 |
| 2 | Y | 1 | 2 |
| 3 | Y | 4 | 2 |
| 4 | Y | 1 | 1 |
| 5 | - | 4 | 7 |
| 6 | - | 3 | 5 |
| 7 | - | 4 | 4 |
Next we select vertex 7 (neighbor of 4, the first chosen neighbor of 1). Its cheapest place in the tree is now known. Now we can adjust vertices 5 and 6. Selecting 5 and 6 doesn't provide any cheaper paths. After 5 and 6 are selected, the Prim's algorithm terminates.
| Known | Path | Length | |
| 1 | Y | 1 | 0 |
| 2 | Y | 1 | 2 |
| 3 | Y | 4 | 2 |
| 4 | Y | 1 | 1 |
| 5 | Y | 7 | 6 |
| 6 | Y | 7 | 1 |
| 7 | Y | 4 | 4 |
To find the minimum spanning tree of the graph featured in the table, follow the Path fields from vertex 1.