Today we are going to study one algorithm for finding the
shortest path between two verticies of a graph. It is known as
Dijkstra's Algorithm. Dijkstra's algorithm is an example of a
Greedy Algorithm. Greedy Algorithms operate by breaking a decision
making process down into small steps, and making the best decision at each
step. For many problems, this approach will lead to the best possible overall
solution -- for others, it will not.
For example, we "make change", by using a greedy algorithm. We hand back
$10 bills, until handing back another $10 would be giving back too
much money. Then we hand out $5 bills, then $1 bills, then quarters,
then dimes, then nickels, then pennies. In the end, we are guaranteed
that we have returned the correct amount of change -- with the fewest
possible bills or coins.
But, this algorithm would not work, for example, if we had 12-cent coins.
Normally, if we have to return 21-cents of change, we return
dime-dime-penny. But, with a 12-cent coin, let's call it the "dozen", we'd
return dozen-nickel-penny-penny-penny-penny. From this example, we
can see that greedy algorithms are appropriate for some problems -- but
not all problems.
But, Dijkstra's Algorithm, is a greedy algorithm -- and does actually work.
It is used to route packets throughout the Internet. Let's discover the magic:
One common use of graphs is to find the shortest path from one place to
another. You may have at some point used an online program to find driving
directions, and you likely had to specify if you wanted the shortest
route/fastest route. This involves finding the shortest path in a weighted
graph. The general algorithm to solve the shortest path problem is known as
Dijkstra's Algorithm.
Dijskstra's createss, in successive steps, a spanning tree, rooted at the
starting vertex. The resulting tree is rooted at this starting vertex
To begin the root vertex v, is selected and it is added to the tree.
At each stage, a vertex is added to the tree by choosing the vertex u
such that the cost of getting from v to u is the smallest
possible cost (the cost might, for example represent a distance in miles).
At each stage, you ask thre question, "Where can I get from here?" and go
down the shortest road possible from where you are.
Applying this algorithm until all vertices of the given graph are in the tree
creates a spanning tree of that graph. And, this spanning tree has the
interesting property that the path from the root to any node has the lowest
possible total/aggegate weight.
Suppose we have the following graph:
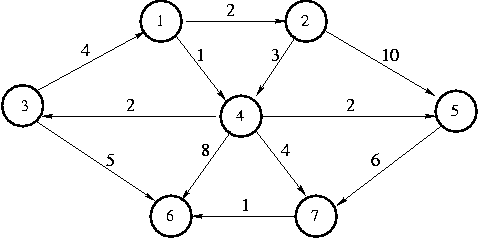
This graph is a directed graph, but it could just as easily be
undirected.
Let's call the starting vertex s vertex 1. Just a reminder
before we begin: the point of a shortest path algorithm is to find the
shortest path to s from each of the other vertices in the graph.
The first vertex we select is 1, with a path of length 0. We mark
vertex 1 as known.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| -
| -
| INF
|
| 3
| -
| -
| INF
|
| 4
| -
| -
| INF
|
| 5
| -
| -
| INF
|
| 6
| -
| -
| INF
|
| 7
| -
| -
| INF
|
The vertices adjacent to 1 are 2 and 4.
We adjust their fields.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| -
| 1
| 2
|
| 3
| -
| -
| INF
|
| 4
| -
| 1
| 1
|
| 5
| -
| -
| INF
|
| 6
| -
| -
| INF
|
| 7
| -
| -
| INF
|
Next we select vertex 4 and mark it known. Vertices 3,
5, 6, and 7 are adjacent to 4, and we can
improve each of their Length fields, so we do.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| -
| 1
| 2
|
| 3
| -
| 4
| 3
|
| 4
| Y
| 1
| 1
|
| 5
| -
| 4
| 3
|
| 6
| -
| 4
| 9
|
| 7
| -
| 4
| 5
|
Next we select vertex 2 and mark it known. Vertex 4 is
adjacent but already known, so we don't need to do anything to it.
Vertex 5 is adjacent but not adjusted, because the cost of
going through vertex 2 is 2 + 10 = 12 and a path of length 3 is
already known.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| Y
| 1
| 2
|
| 3
| -
| 4
| 3
|
| 4
| Y
| 1
| 1
|
| 5
| -
| 4
| 3
|
| 6
| -
| 4
| 9
|
| 7
| -
| 4
| 5
|
The next vertex we select is 5 and mark it known at cost 3.
Vertex 7 is the only adjacent vertex, but we don't
adjust it, because 3 + 6 > 5. Then we select vertex 3, and adjust the
length for vertex 6 is down to 3 + 5 = 8.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| Y
| 1
| 2
|
| 3
| Y
| 4
| 3
|
| 4
| Y
| 1
| 1
|
| 5
| Y
| 4
| 3
|
| 6
| -
| 3
| 8
|
| 7
| -
| 4
| 5
|
Next we select vertex 7 and mark it known. We adjust vertex 6
down to 5 + 1 = 6.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| Y
| 1
| 2
|
| 3
| Y
| 4
| 3
|
| 4
| Y
| 1
| 1
|
| 5
| Y
| 4
| 3
|
| 6
| -
| 7
| 6
|
| 7
| Y
| 4
| 5
|
Finally, we select vertex 6 and make it known. Here's the final table.
|
| Known
| Path
| Length
|
| 1
| Y
| 1
| 0
|
| 2
| Y
| 1
| 2
|
| 3
| Y
| 4
| 3
|
| 4
| Y
| 1
| 1
|
| 5
| Y
| 4
| 3
|
| 6
| Y
| 7
| 6
|
| 7
| Y
| 4
| 5
|
Now if we need to know how far away a vertex is from vertex 1,
we can look it up in the table. We can also find the best route, for
example, from the starting city (the one we selected as the route) to
any other city (any other node). We just use the Path field to find
the destinations predecessor, then use that node's path field to find
its predecessor, and so on.
Unweighted graphs are a special case of weighted graphs. They can
be addressed using Dijkstra's algorithm, as above -- just assume
that all of the edges weigh the same thing, such as 1. Or, we
can actually take a little bit of a shortcut.
For unweighted graphs, we don't actually need the "known" column
of the table. This is because as soon as we discover a path to a
vertex, we have discovered the best path -- there is no way we
can find a better path. As a result, the verticies become
"known" as soon as we find the first way to get there. We might
subsequently find an equally good way -- but never a better way.
Let's think about the situation in Dijkstra's Algorithm that resulted
in the discovery of a "better" path to a vertex that was already
reachable. This situation occured, if a path with more "hops"
was shorter than a path with fewer "hops". In other words, Dijkstra's
algorithm reaches nodes in the same order as a breadth-first search
-- reaching all nodes one hop from the start, then those two hops from
the start, then those three hops from the start, and so on.
But, since not all of the hops are of the same length, one hop
might be really long, for example it might have a cost of 100.
But, another path between the same nodes, might involve three hops,
of lengths, 10, 20, and 30. It is cheaper to go the three hops
10+20+30=60 than the single hop of 100. Yet, the hop of 100 is
the path that is discovered first. As a result, we need to
check subsequent paths that pass through more verticies, until
we are sure that we can't find a better path, at which time,
we finally mark the node (and the path to it) as known.
Since, in an unweighted graph, all of the edges are modeled as
having the same weight, it is impossible for this situation
to occur. Two hops will always be longer than three hops, &c.
Since the algorithm is proceeding in a depth-first fashion,
we find things that are one hop away before things that are two
hops away, before things that are three hops away, and so on.
As a result, in an unweighted graph, as soon as we find a node,
it is known -- there can be no better way of finding it.
Let's consider an example for the graph shown below.
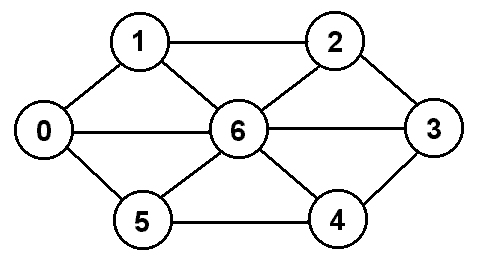
We would build a table as follows:
|
| Known
| Path
| Length
|
| 0
| -
| -
| INF
|
| 1
| -
| -
| INF
|
| 2
| -
| -
| INF
|
| 3
| -
| -
| INF
|
| 4
| -
| -
| INF
|
| 5
| -
| -
| INF
|
| 6
| -
| -
| INF
|
In the table, the index on the left represents the vertex we are going to
(for convenience, we will assume that we are starting at vertex 0).
This time, we will ignore the Known field, since it is only necessary
if the edges are weighted. The Path field tells us which vertex precedes
us in the path. The Length field is the length of the path from the
starting vertex to that vertex, which we initialize to INFinity under the
assumption that there is no path unless we find one, in which case the length
will be less than infinity.
We begin by indicating that 0 can reach itself with a path of length 0.
This is better than infinity, so we replace INF with 0 in the Length column,
and we also place a 0 in the Path column. Now we look at 0's
neighbors. All three of 0's neighbors 1, 5,
and 6 can be reached from 0 with a path of length 1
(1 + the length of the path to 0, which is 0), and for all
three of them this is better, so we update their Path and Length fields,
and then enqueue them, because we will have to look at their neighbors next.
We dequeue 1, and look at its neighbors 0, 2,
and 6. The path through vertex 1 to each of those vertices
would have a length of 2 (1 + the length of the path to 1, which is 1).
For 0 and 6, this is worse than what is already in their Length
field, so we will do nothing for them. For 2, the path of length 2 is
better than infinity, so we will put 2 in its Length field and 1 in
its Path field, since it came from 1, and then we will enqueue so
we can eventually look at its neighbors if necessary.
We dequeue the 5 and look at its neighbors 0, 4, and
6. The path through vertex 5 to each of those vertices would
have a length of 2 (1 + the length of the path to 5, which is 1).
For 0 and 6, this is worse than what is already in their
Length field, so we will do nothing for them. For 4, the path of
length 2 is better than infinity, so we will put 2 in its Length field and
5 in its Path field, since it came from 5, and then we will
enqueue it so we can eventually look at its neighbors if necessary.
Next we dequeue the 6, which shares an edge with each of the other six
vertices. The path through 6 to any of these vertices would have a
length of 2, but only vertex 3 currently has a higher Length
(infinity), so we will update 3's fields and enqueue it.
Of the remaining items in the queue, the path through them to their neighbors
will all have a length of 3, since they all have a length of 2, which will be
worse than the values that are already in the Length fields of all the
vertices, so we will not make any more changes to the table. The result is
the following table:
|
| Known
| Path
| Length
|
| 0
| -
| 0
| 0
|
| 1
| -
| 0
| 1
|
| 2
| -
| 1
| 2
|
| 3
| -
| 6
| 2
|
| 4
| -
| 5
| 2
|
| 5
| -
| 0
| 1
|
| 6
| -
| 0
| 1
|
Now if we need to know how far away a vertex is from vertex 0, we can
look it up in the table, just as before. And, just as before, we can use the
path field to discover the rout from the starting node to any vertex.

