Introduction to Binary Search Trees (BSTs)

The next data structure that we'll examine is known as a Binary Search Tree, most often known simply as a BST. The theory of operation is going to be basically the same as that of the binary search, except that it'll be a little more "relaxed".

Instead of building the entire tree in advance, by sorting the list of numbers using something like quick sort or selection sort, we are going to build it "as we go along", by inserting the numbers into the tree. This is very similar to, for example, using insertion sort instead of selection sort.

But, unlike using insertion sort as the basis for a binary search, we're going to do something a little faster -- but a little less exact. Let's take a look:

How Do Binary Search Trees (BSTs) Work?

BSTs are trees. Each node of the tree is much like a node of a doubly linked list. It contains a value, and references to up to two other nodes. Each fo these nodes, in turn, contains a value and a reference to up to two other nodes. We call these other nodes the left and right children.

The idea is that each node represents some point within a sorted list. To the left of this point lie values less than it. To the right of this point lie values greater than it. It is important to realize that there might be no value in either direction, or the node in that direction might, itself have children.

But, since this property can be applied recursively, we known that all of the nodes to the left of a particular node, even if they are children of (below) another node, are less than the node. The same goes for all of the nodes to the right.

One way of thinking of this is that each node is the root of two subtrees: the left subtree and the right subtree. Everything in the left subtree is less than the root. Everythign in the right subtree is greater than the root.

The important thing about this arrangement is that we can, as we did before, work our way form the top (root) of this tree to the bottom, dividing the list each time, so we can discard all of the possibilities in one direction or the other.

Constructing a Binary Search Tree

Let's construct a binary search tree using by inserting the letters of "HELLO WORLD" into the tree one at a time. For convenience, we will ignore duplicate letters.

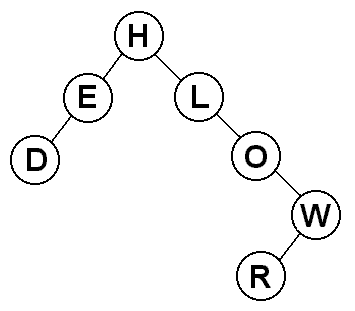
How did this work? Let's go through the string one letter at a time.

• "H" - the tree is initially empty, so "H" becomes the root
• "E" - "E" comes before "H", so it goes on the left
• "L" - "L" comes after "H", so it goes on the right
• "L" - "L" is already in the tree, so we ignore it
• "O" - "O" is greater than "H", so it goes to the right of it, and it is greater than "L", so it goes to the right of that, too
• "W" - "W" is greater than "H", so it goes to the right of it, it is greater than "L", so it goes to the right of that, and it is greater than "O", so it goes to the right once again
• "O" - "O" is already in the tree, so we ignore it
• "R" - "R" comes after "H", "L", and "O", so it goes to the right of all of them, and then it comes before "W" so it goes to the left of it.
• "L" - "L" is already in the tree, so we ignore it
• "D" - "D" comes before "H", so it goes to the left of it, and it also comes before "E", so it goes to the left of that, too.

The result is the tree you see. If you look at any node in the tree, you will see that the binary search tree ordering property holds.

An Example of Using A Binary Search Tree?

Suppose we're looking for the letter F in the "HELLO WORLD" tree. We can immediately eliminate everything to the right of the H, because we know that F can't be there because F comes before H. We move on to E, and we can eliminate everything on its left, because we know that it can't be there because it comes after E. E's right child is null, so we have determined that F is not in the tree by only looking at 2 of the 7 nodes.

How Much Does It Cost?

How many nodes do we have to look at in a tree before we know that an item is not in the tree? To simplify this, we will only look at the best possible trees of a given size. These best trees are complete and balanced, meaning that the path from the root to the farthest leaf is at most one step longer than the path from the root to the closest leaf. The following are examples of balanced trees:

So how many nodes do we have to look at in the worst case? If there are N nodes in the tree:

N nodes	# looked at
1	1
2	2
3	2
4	3
5	3
6	3
7	3
8	4

You can probably see a pattern here. The number of items you need to look at grows every time we reach a power of 2. We would only need to look at 4 items for trees with between 8 and 15 nodes and then we would have to look at 5 items in a tree with 16 nodes. This is known as logarithmic growth, and we can create a formula for the number of items we need to look at in a tree with N nodes.

# items = (log₂ N) + 1

The Costs of a BST

In a tree with 1,000,000 nodes, we would only need to look at 20 nodes to insert or find a node. This is a significant improvement over a linear search and comparable to sorting a list and performing a binary search.

But, in practice, it is much cheaper than sorting a vector, for example using a insertion sort. This is because, if we can accurately capture the tree representation with a data structure, we don't need to "push back" every other node for an insert.

The flip side is that the worst case is bad -- it could degenerate to a linear search of a linked list. Much like a quick sort, this technique is not stable -- but, given typical data performs comparably with the best case.

Now, let's take a look at building a BST class.

The Comparable Interface

As we start developing code to implement Binary Search Trees, we're going to need a way of comparing different Objects. The Java Comparable interface provides this functionality in the form of the compareTo() method. So, instead of dealing with Objects, our trees will store Comparable Objects -- only those Objects that implement the Comparable interface. Although you have used the compareTo() method in lab, we never did formally introduce it in lecture -- so we'll do that now.

The Comparable Interface defines only one method: int compareTo(Object o).

Let's consider a.compareTo(b). In this case, compareTo() will return 1 if a is greater than b, 0 if the two are equal, or -1 if a is less than b.

Remember, the compareTo() method must be defined in each Object that implements the Comparable interface. It is in this definition where the implementor of how the particular type of Object is compared.

The Big Picture

Much like our LinkedList and DoublyLinkedList classes, our BST will require two related classes: a BSTNode to represent the data and the left and right subtrees, and the BST, itself, which will contain the root of the tree and all of the methods, such as insert() and find(), that manipulate it. c

The root of the BST class serves a very similar purpose to the head of the LinkedList -- it gives us a place to start. And the left and right references within the BSTNode are analagous to the prev and next references within a doubly linked list node. They name other, related, nodes that are part of the tree structure. And, as before, the data member will be accessible, but immutable. The other references within the BSTNode will be mutable.

Inserting Into A Binary Search Tree

We already went through the process of building a tree when we created the "HELLO WORLD" tree, so now let's take a look at some code to perform the insertion. Since trees are naturally recursive, we will use recursion. The root parameter in this code is the current subtree, not necessarily the root of the original tree. We search for the position to insert the new node, by cutting the original tree in half with each examination, and determining which half to search. We then call the insert method recursively on the correct half of the tree, by passing it either the left child or the right child of the root from the previous recursive activation.

// "root" here is the root of the current subtree
void BSTinsert(BinaryTreeNode root, Comparable data)
{
   // if the tree is initially empty, the data we
   // add becomes the root of the tree
   if (null == this.root)
   {
      this.root = new BinaryTreeNode(data);
      return;
   }

   // if the current data matches the data we want to
   // insert, it is already in the tree so we ignore it
   if (root.data().compareTo(data) == 0)
   {
      return;
   }

   // if the current data is greater than the one we
   // want to add, we need to go to the left
   if (root.data().compareTo(data) > 0)
   {
      // if the left is null, we can add data there
      if (root.left() == null)
      {
         root.setLeft(new BinaryTreeNode(data));
         return;
      }
      // if not, we need to recursively insert into the
      // subtree on the left
      else
      {
         BSTinsert(root.left(), data);
         return;
      }
   }
   // if the current data is less than the one we want
   // to add, we need to go to the right
   else
   {
      // if the right is null, we can add data there
      if (root.right() == null)
      {
         root.setRight(new BinaryTreeNode(data));
         return;
      }
      // if not, we need to recursively insert into the
      // subtree on the right
      else
      {
         BSTinsert(root.right(), data);
         return;
      }
   }
}
  

Searching in a Binary Search Tree

As with insert(), this is implemented recursively. It returns the data, if found, or throws an exception, otherwise.

Comparable BSTfind(Node root, Comparable findMe) throws NotFoundException
{
   // if the current subtree is null, the findMe
   // can't possible be in it
   if (null == root)
   {
      thrown new NotFoundException("Item not found in BST.")
   }

   // if the current data matches findMe, we have
   // found it so we can return it
   if (root.data().compareTo(findMe) == 0)
   {
     return root.data();
   }

   // if the current data is greater than findMe, then
   // if findMe is in the tree it must be to the left,
   // so we will recursively search the left subtree
   if (root.data().compareTo(findMe) > 0)
   {
      return BSTfind(root.left());
   }
   // if the current data is less than findMe, then
   // if findMe is in the tree it must be to the right,
   // so we will recursively search the right subtree
   else
   {
      return BSTfind(root.right());
   }
}

Implementing Delete

Last class, we finsihed up by discussing the algorithm for deleting a node within a BST. Today, we walked through the implementation together:

  public void delete (Comparable c)
{
        root = delete(root, c);
}

/*
 * A recursive method that will copy the correct data into the node to
 * be deleted, and then call delete on the node where it got that data.
 * The method will continue to go recursively, until it is called to delete
 * a leaf, in which case it merely makes the reference to that node null.
 */
private static BinaryNode delete (BinaryNode bn, Comparable c)
{
        if (null == data) return root;

        if (null == root) return null;

        if (data.compareTo(root.getData()) == 0)
        {
                if (root.isLeaf()) return null;

                if (root.getLeft() == null) return root.getRight();

                if (root.getRight() == null) return root.getLeft();

                Comparable replacementData = getRightmost(root.getLeft());

                return new BinaryNode (/* data */ replacementData,
                                       /* left */ delete(root.getLeft(), replacementData),
                                       /* right */ root.getRight());
        }

        else if (data.compareTo(root.getData()) < 0)
        {
                root.setLeft(delete(root.getLeft(), data));
                return root;
        }

        else
        {
                root.setRight(delete(root.getRight(), data));
                return root;
        }
}

/*
 * The method to find the rightmost node in the left subtree.
 * It is used to find the proper data to put in the node to be deleted.
 */
private BinaryNode getRightmost(BinaryNode bn)
{
        // Special case: empty tree
        if (null == bn)
                return null;

        // Special case: no right child
        if (null == bn.getRight())
                return bn;

        // Common case: Go right
        return getRightmost(bn.getRight());
}