Trees

So far this semster, we've discussed a few different ways of organizing information. Initially, we reviewed 15-100: we talked about the simple case: simple, single, items, and aggregations there of. Then, we talked about indexed lists: The array and corresponding ArrayList. Next, we talked about linked lists: sequential but unindexed lists.

Today, we are going to talk about trees. Trees are data structures defined by the parent-child relationship. A node of a tree can have many children, but exactly one parent. In most trees, there is a single distinguised node, or a "starting point", much like the head of a linked list. We call this distinguished node the root of the tree. By convention we draw the root of the tree, in trees that have a root, at the top. Take a look at the tree below:

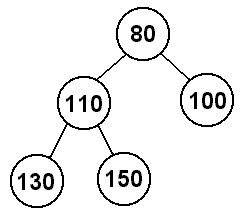
We see the root node, 80, at the top. Notice that the root is the only node without any children. Notice also that nodes 100, 130, and 150 have no children. We call these these nodes leaves. Any node without children is called a leaf. It is possible for the root node to be a leaf. Any node with children is known as an interior node. The root can be either an interior node or a leaf.

In talking about trees, the terms heightdepth are easily confused. We talk about the depth of a leaf. The depth of a leaf is the distance between the leaf and the root. The depth between the root and itself is 0. In our example above, the dpeth of 110 is 1 and the depth of 150 is 2.

The height of a tree is the depth of its deepest node. So, paradoxically, a tree with a single node has a height of 0. The height of an empty tree is undefined, as there is nothing to measure.

It is important to note that a node's descendant can never be an ancestor. This would create what we call a cycle, or a loop. Trees cannot have cycles. It is also worth noting that trees don't necessarily have to have a distinguisehd node. It is possible to have a rootless tree, but these are beyond the scope of 15-111, to be sure.

In 15-111, we are going to discuss only one type of tree: The Binary Tree. A binary tree is a tree in which a node can have at most two children, hence binary. Binary trees are straight-forward to represent and are extremely useful for many types of problems.

Expression Trees

An expression tree is a binary tree which is used to represent a mathematical expression. For example, if we have the expression (2 * (4 + (5 + 3))), we could construct a tree to represent it.

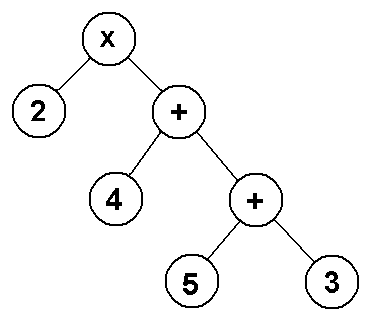
In an expression tree, the parent nodes are the operators, and the children are the operands. To find the result of this expression, we need to first solve (5 + 3), which is 8, then solve (4 + 8), which is 12, and then finally solve 2 * 12, which is 24. So our root node will contain the operator within the outermost set of parentheses, it's left child will be the value "2", and the right child will be the remaining expression that needs to be solved, which would be (4 + (5 + 3)).

When we talked about solving expressions using stacks, we had three different ways we could represent an expression: infix, where the operator comes between its two operands; prefix, where the operator comes before its two operands; and postfix, where the operator comes afters its two operands. Given an expression tree, we can generate any of those representations using one of the three traversals of a binary tree: in-order, pre-order, and post-order.

In-Order Traversal

In an infix expression, the operator comes between its operands, so if we want to generate the infix expression from an expression tree, we will need to print the operand on the left before we print out the operator. But what if the left operand is another expression to evaluate? We use recursion. We print out the entire left subtree, then print the current node, then print out the entire right subtree.

void inOrder(BinaryTreeNode root)
{
        if (null == root) return;

        inOrder(root.left());   // print the entire left subtree

        System.out.println(root.data());

        inOrder(root.right());  // print the entire right subtree

        return;
}
  

In this code, "root" refers to the root of the current subtree, not the root of the whole tree (although we would have to start at the root of the whole tree). So, how does this work? Let's look at the steps that this method takes for the simple expression 5 + 3 (for convenience, the nodes have been numbered:

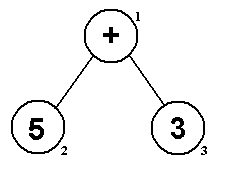
1. We start by calling inOrder(1) (the root)
2. (1) is not null, so we call inOrder(2) (1's left)
3. (2) is not null, so we call inOrder(2's left)
4. (2)'s left is null, so it just returns back to (2)
5. We've done the left, so now we print the data at (2), which in this case is "5"
6. we've printed (2), so now we call inOrder(2's right)
7. (2)'s right is null, so it just returns back to 2
8. (2) has now finished, so it returns back to (1)
9. we've printed (1)'s left, so now we print the data at (1), which in this case is "+"
10. we've printed (1), so now we call inOrder(3)
11. (3) is not null, so we call inOrder(3's left)
12. (3)'s left is null, so it just returns back to (3)
13. We've done the left, so now we print the data at (3), which in this case is "3"
14. we've printed (3), so now we call inOrder(3's right)
15. (3)'s right is null, so it just returns back to (3)
16. (3) has now finished, so it returns back to (1)
17. (1) has now finished, so the result is "5+3", which is the infix representation of the tree

Pre-Order Traversal

We can generate a prefix expression using a pre-order traversal. Much like for the in-order traversal, we will use recursion to print the entire left subtree and the entire right subtree. In a prefix expression, the operator comes before its two operands, so we will have to print out the parent node's data before recursively printing its left and right children.

void preOrder(BinaryTreeNode root)
{
        if (null == root) return;
        
        System.out.println(root.data());
        
        preOrder(root.left());   // print the entire left subtree
        
        preOrder(root.right());  // print the entire right subtree
        
        return;
}
  

So, instead of printing the data after we have printed the left subtree, we are going to print the data first, so that the operator will print out before its operands, giving us the prefix representation of the expression.

Post-Order Traversal

By now, you should see a pattern. The last representation is postfix, and we will use a post-order traversal to obtain it. Since in postfix the operator comes after its two operands, will recursively print the left and right subtrees before we print out the data at the current node.

void postOrder(BinaryTreeNode root)
{
        if (null == root) return;
        
        postOrder(root.left());  // print the entire left subtree
        
        postOrder(root.right()); // print the entire right subtree
        
        System.out.println(root.data());
        
        return;
}
  

Level-order traversal

Try to think about a way to traverse a tree and visit its nodes in level order. In other words print the root, then everything at level 2 (children of the root), then everything at level 3 (children of level 2).

It is true that this is the natural result of a linear walk through the vector representation of a tree. But, please don't approach the problem that way. Try to find an algorithmic solution with the same flavor as the traversals we covered today -- one that would work somewhat independent of the representation.

Let's observe that our goal can be accomplished if we "look one level down the tree". In other words, the parent can see its children, but the children, the siblings, can't see each other. Given this, it is clear that the parent needs to drive the process.

So, here's what we are going to do. We are going to approch this iteratively. We are going to maintain a queue of verticies, inserting them by level, from left-to-right. So, when we visit a node, we will enqueue its children.

We get things started by enqueuing the root. Once we've done that, we enter our main work loop. Each iteration, we will dequeue a node -- the node that we are visiting. At this point, we will consider it visited and print it out, or whatever. Then, we will enqueue its children. By doing this, all nodes at level n are enqueued, and will be processes, before any deeper node at level n + 1 or greater. We continue this loop, until we've processed all of the nodes -- the queue is empty.

The pseudocode below ignores some Java details for clarity, but should communicate the algorithm well.

  void levelOrder (BinaryTreeNode root)
  {
    if (root == null) // Problem case
      return; 

    // Initialize the queue
    Queue levelQueue = new Queue();
    levelQueue.enqueue (root);

    // Process nodes, until we've got them all
    while (!levelQueue.isEmpty())
    {
      root = levelQueue.dequeue();
      System.out.println (root.data());
      
      if (root.left() != null)
        levelQueue.enqueue(left);
      
      if (root.right() != null)
        levelQueue.enqueue(right);
    }
  }