Effective Nuclear Charge:

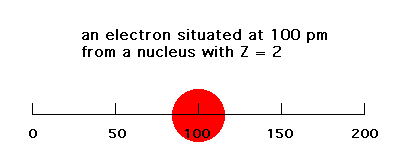
The electrostatic energy of attraction between a single negative charge (electron) and Z units of positive charge is given simply by -Ze²/r. Here, r is the distance between the electron and the nucleus. In the Bohr planetary model, r is fixed. In reality, the electron is diffusely spread over a range of r values. We'll look at a one-dimensional, simplified "model" of this electrostatic energy of attraction. If the electron is at a distance of 100 pm from a nucleus with Z = 2 (like He, if this were three-dimensional), the energy would be -Ze²/100 = -e²/ 50 (ignoring units since we'll be making comparisons only). If that electron were at a distance of 200 pm, the energy of attraction would be -Ze²/200 = -e²/100.

Now put a second electron into our system. If the first electron were at r = 100 pm and the second electron were at r = 200 pm, that second electron would feel a net attraction due to Z-1 positive charges because of screening (shielding) of the closer negative charge. The second electron's energy of attraction would then be -(Z-1)e²/200 = -(2-1)e²/200 = -e²/200. Since our expression for attraction of one electron was -Ze²/r, this second electron thinks it is attracted by a Z = 1 nucleus since for Z = 1 and r = 200 pm you get that energy = -e²/200. But the nucleus we established has Z = 2. Hence, in this circumstance, we refer to the effect of the nucleus and the other, first electron by saying the effective nuclear charge on electron #2 is 1, or Z_eff = 1.

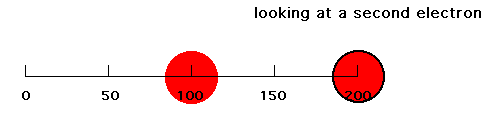
But this is an oversimplification for electron density distributions which are spread out. Now suppose our first electron had an average distance from the nucleus of 100 pm, but that 25% of its radial distribution was near 50 pm, 50% was near 100 pm, and 25% was near 150 pm as pictured below.

The second electron would also have a diffused radial distribution. First, let's explore how the energy of attraction of the second electron varies as we move that electron around. If electron #2 is at 200 pm, we still get the energy of attraction to be our previous value of -e²/200. This value also pertains to r for electron #2 all the way in to 150 pm.

When we move electron #2 just inside a distance of 150 pm, it is now screened by only three-fourths of the charge distributed by electron #1. This gives an energy of attraction of -(Z-3/4)e²/r = -(2-.75)e²/150 = -e²/121 (keeping the form of the answer as was presented above). Since the electron is at a distance of 150 pm here, we have an effective positive charge of Z-.75 = 1.25 = Z_eff for this arrangement. We can ignore any electrostatic effect on the outside of where electron #2 is located.

If we move electron #2 down just inside 100 pm, it is screened by 25% of electron #1's charge giving an energy of attraction of -(Z-1/4)e²/100 = -(2-.25)e²/100 = -e²/57.1. Now the effective positive charge attracting the electron is 1.75 = Z_eff.

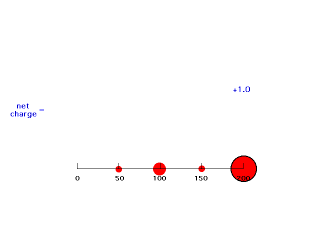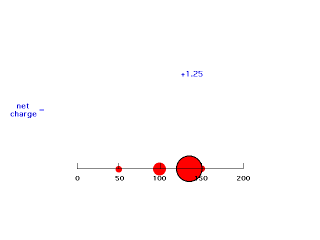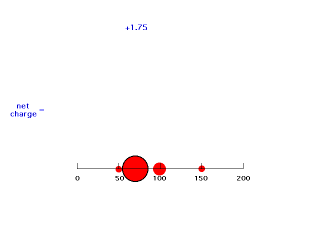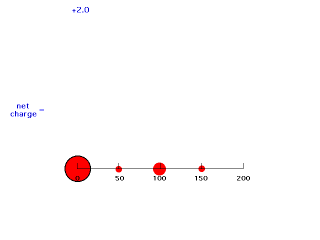
If we move electron #2 inside 50 pm, it is not screened at all by negative charge between itself and the Z positive charges of the nucleus so its energy of attraction is -(Z-0)e²/50 = -e²/25 and Z_eff = Z = 2. The animation below moves electron #2 (outlined in black) in towards the nucleus of charge +2 and shows how the net positive charge varies with distance in this artificial scheme.

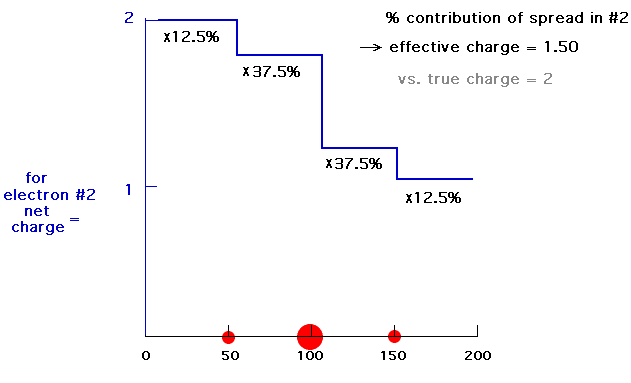
Our last step is to say that electron #2 also has its distribution spread out. Let's say, for the sake of illustration, 12.5% beyond 150 pm, 37.5% just inside 150 pm, 37.5% just inside 100 pm, and 12.5% just inside 50pm. For each of these, we already looked at the net charge attracting electron #2. From the above, these net positive charges were 1, 1.25, 1.75, and 2. But now we average them according to their contributions to the overall distribution of electron #2 and get (12.5%)(1) + (37.5%)(1.25) + (37.5%)(1.75) + (12.5%)(2) = 1.50. This is the overall effective nuclear charge, Z_eff, attracting electron #2 to the system.