| Lecture
#6 |
| |
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
| Lecture Outline |
Many-electron systems
Pauli Exclusion Principle
Photoelectron spectra, ionization energies and Zeff
Hund's Rule
Electron configurations
|
Another mathematical consequence of wave
behavior can be expressed in a simple statement. This is
crucial as soon as we deal with more than one electron.
|
 |
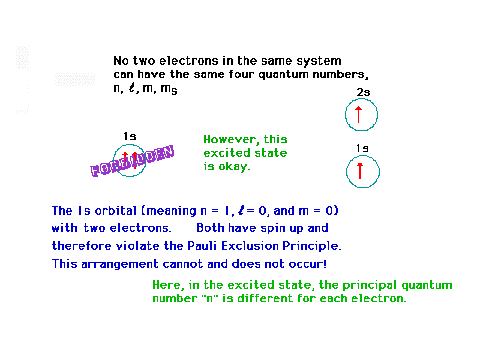
| Illustrating the Pauli Principle for two
electrons. |
 |
| Continuing with our illustratiion of two
electrons. |
 |
| More discussion on two electrons. |
 |
| A reminder that an electron in a 2s orbital has
a different distribution with respect to the nucleus
(origin) than when it is in the 2p orbital. |
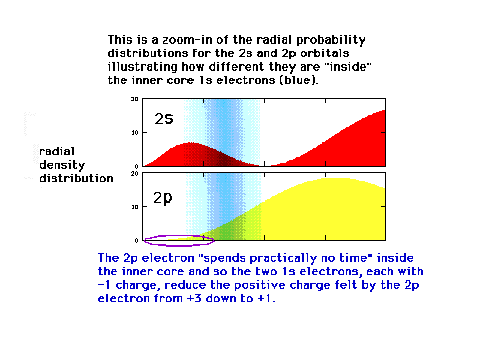 |
| A 2s electron will be attracted by a greater
net positive charge than a 2p electron because of the
different effectiveness of the screening by inner core
electrons. |
 |
| Unlike one electron systems where the 2s and 2p
orbitals have exactly the same energy, in many-electron
systems, the 2s is lower in energy than the 2p. |
 |
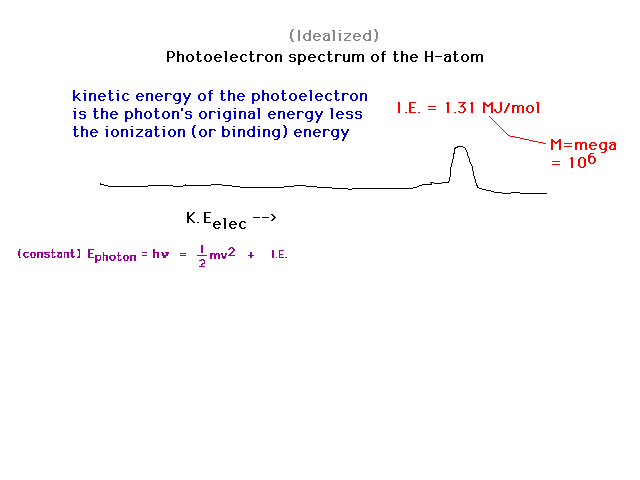
| Recalling that the photoelectric effect can be
exploited to obtain "binding energies" of an
electron to some anchor (metal surface, gaseous molecule
or atom), we can look at binding energies of an electron. |
 |
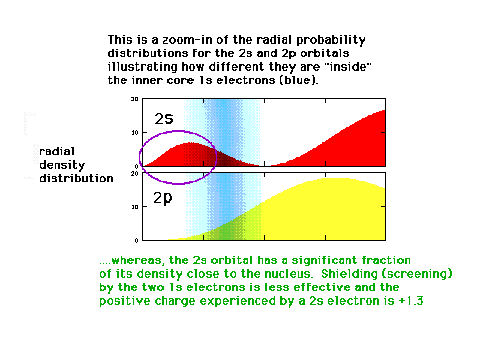
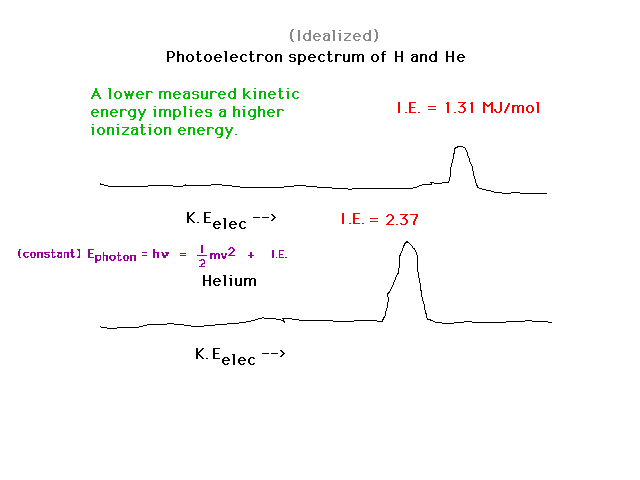
| When we go from H to He, despite the fact that
the nuclear charge has doubled and that Bohr's energy
formula suggests the binding energy might then have
quadrupled, it increases by only 80%. You should be able
to show that the effective nuclear charge holding a 1s
electron in He is about 1.3. |
 |
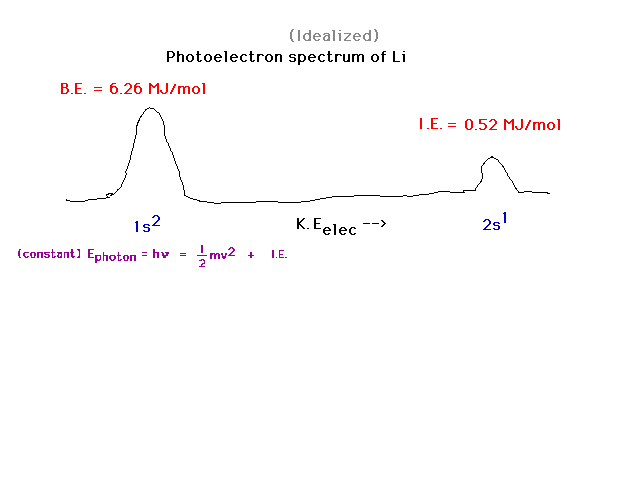
| For element number 3, we note two photoelectron
peaks, one from each of the orbitals containing
electrons. Depending on which single electron is ejected
by the photon, the electron has one of two possible final
kinetic energies. |
 |
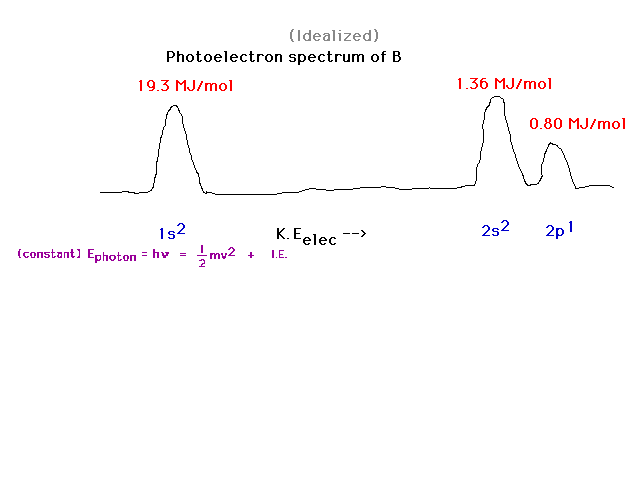
| Boron is element 5. There are 5 electrons distributed
as: two in the inner core, 1s orbital; 2 in the valence
2s orbital; and 1 in the valence 2p orbital. The latter
is easiest to remove and, when kicked out by the photon,
shows up with the greatest kinetic energy therefore. |
 |
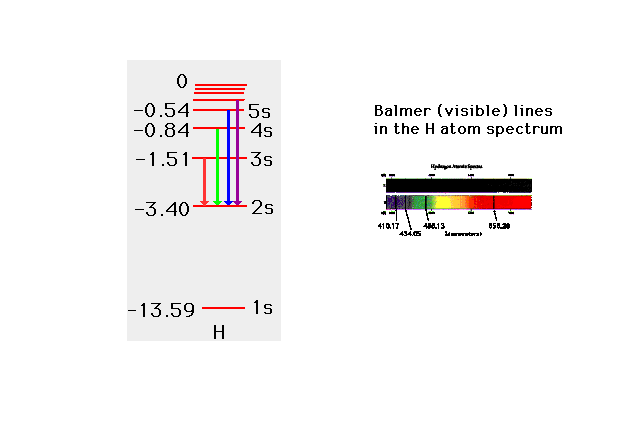
| The enery levels of the one electron in
the hydrogen atom. |
 |
| The energy levels of the various
s-states in a one-electron system. The energy needed to
remove an electron from hydrogen in its "ground
state" is shown. This can be determined through
photoelectron spectroscopy (an application of the
photoelectric effect), for example. |
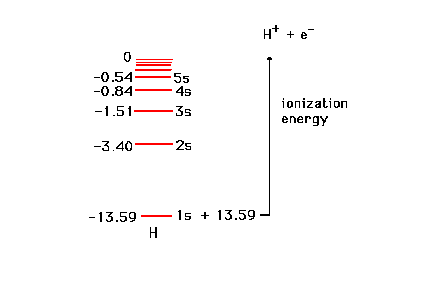 |
| From the values of the electrons's energies,
you can also get the photon energies (and wavelengths)
involved in transitions between initial and final
electron states. |
 |
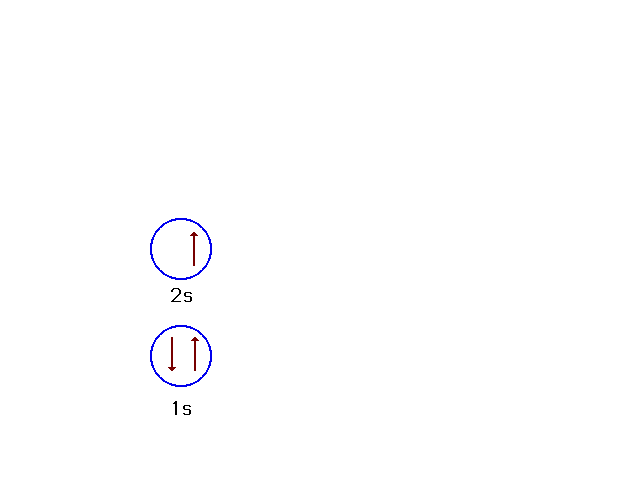
| Consider lithium's ground state (Z=3).
The "inner core" of electrons comrpises the
filled 1s shell. The "outer electrons" are the
valence electrons. In this case, the 2s electron is the
valence electron for lithium. |
 |
| We can indicate how electrons are placed in
orbitals by configuration diagrams. The one shown here
corresponds to the ground state for lithium (Z=3). |
 |
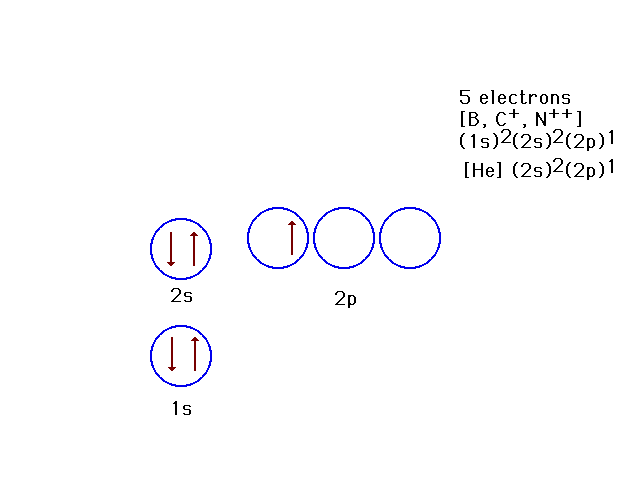
| Because the effective nuclear charge is
determined by how much the nucleus is screened by other
electrons, the 2p orbitals are not as tightly bound as
the 2s orbital. This is the ground state for 5-electron
systems. |
 |
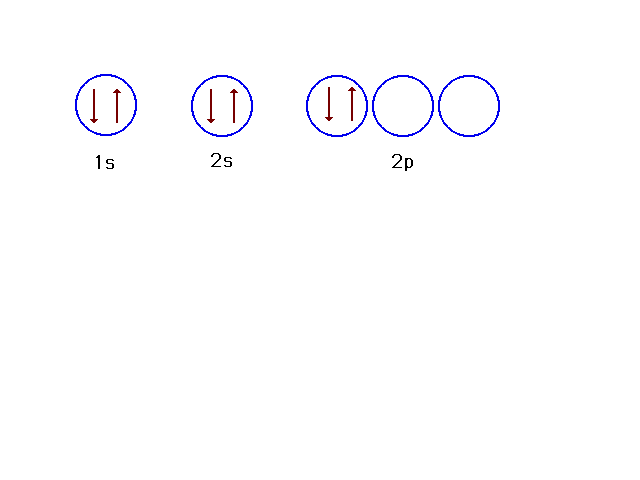
| The arrangement of orbitals in increasing
energy can be shown horizontally too, as in the text. For
the sixth electron, there are several locations to chose
from. This is the lowest energy choice, the most stable. |
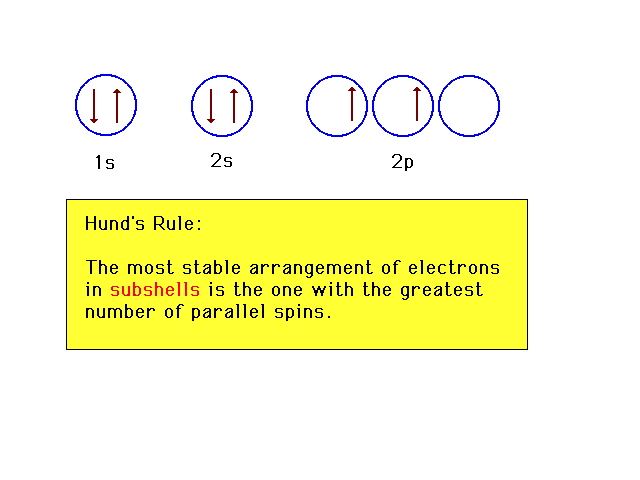 |
| This arrangement is another possible choice for
6 electrons, but is an excited state for a 6-electron
system. |
 |
| The arrangement of orbitals in increasing
energy can be shown horizontally too, as in the text. For
the sixth electron, there are several locations to chose
from. This is the lowest energy choice, the most stable. |
 |
| This arrangement is another possible choice for
6 electrons, but is an excited state for a 6-electron
system. |
 |
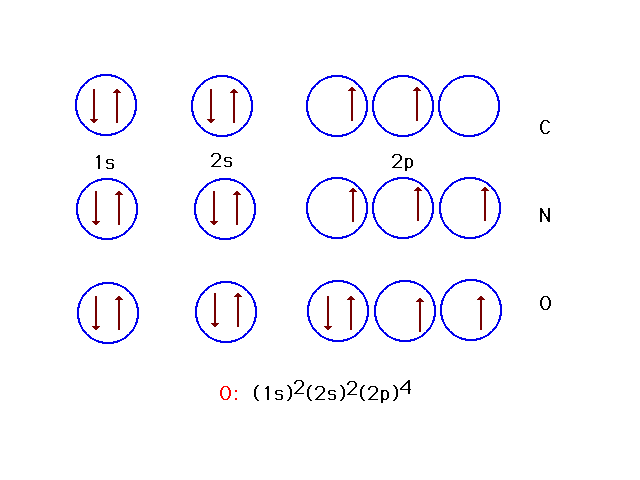
| Here are seven and eight electron systems (in
addition to six) corresponding to ground state
arrangements of electrons in nitrogen and oxygen. On the
last line is written another form of the electron
configuration for atomic oxygen in its ground state. |
 |
| Other electron configuration examples:
fluorine and sodium. |
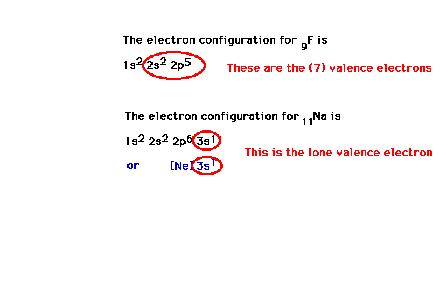 |
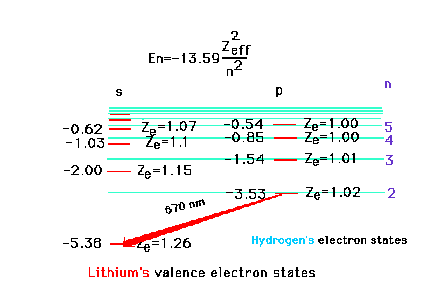
| Excited states for the valence electron
in lithium |
 |
| The idea that an effective nuclear
charge can embody all the various "penetration"
and "screening" effects due to the many
electrons around an atomic nucleus. Penetration refers to
an electron having some of its density inside the region
where inner core electrons are most likely to be found.
Screening refers to the reduction of positive charge felt
by an outer electron due to the presence of inner,
negatively charged electrons. |
 |
| The ionization energy of the highly
excited valence electron, starting in the 5s state of
lithium, corresponds very closely to the ionization
energy of a hydrogen atom which has Z = 1. This is
because the lithium 5s electron is far away from the
nucleus with charge +3 and the inner core of electrons
which contribute a charge of -2 and through which the
far-away electron penetrates only very slightly. |
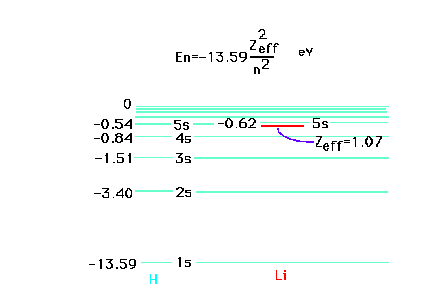 |
| That excited valence electron, if in a
p-orbital, penetrates the inner core even less than if an
s-orbital. The effective nuclear charge is much closer to
unity. The effectiveness of penetration decreases as the
electron in question moves to higher and higher orbitals.
The transition shown corresponds to 2p --> 2s and
involves red light. |
 |