| Lecture
#6 |
 Textbook
Chapter 12 now Textbook
Chapter 12 now  No! No!
No! (That's Bohr's picture) No! No!
No! (That's Bohr's picture) |
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
| Lecture outline |
More outcomes of wave-particle
duality
(Heisenberg's) Uncertainty Principle
simultaneous precise measurements restrictions
paths or orbits of particles are not
legitimate topics of discussion
One-electron systems
Radial density distributions
Many-electron systems
Pauli Exclusion Principle
electron configurations
|
| The 1s wave function (or probability amplitude) as a
function of distance from the nucleus. |
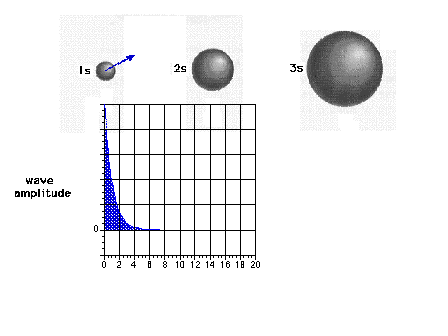 |
| The square of the 1s wave function or the probability
density of the electron in a 1s state |
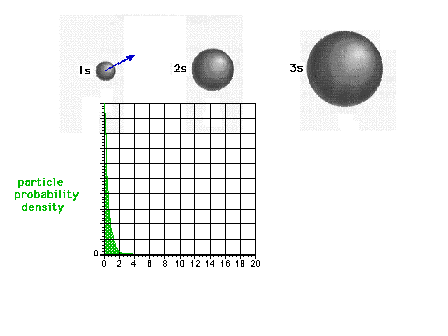 |
| The 2s wave function (or probability amplitude) as a
function of distance from the nucleus. |
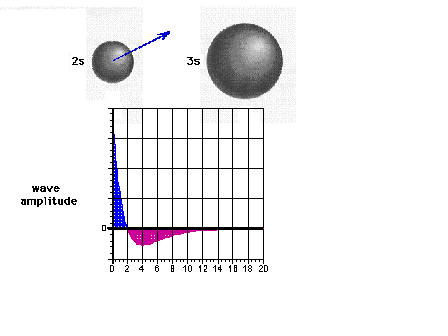 |
| The square of the 2s wave function or the probability
density of the electron in a 2s state |
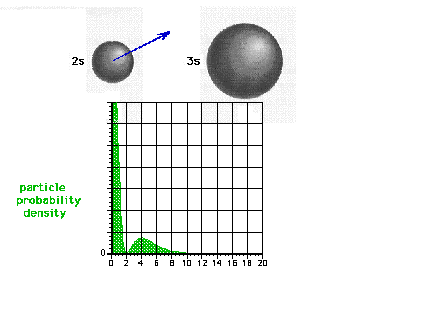 |
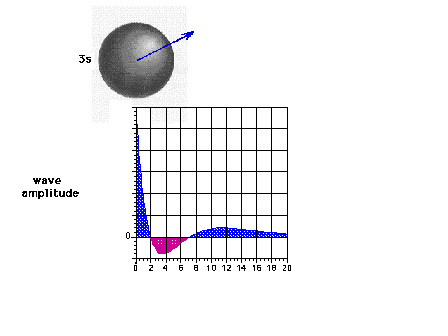
| The 3s wave function (or probability amplitude) as a
function of distance from the nucleus. |
 |
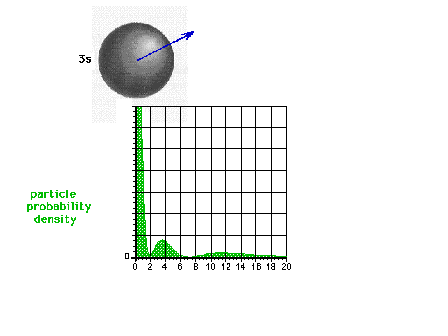
| The square of the 3s wave function or the probability
density of the electron in a 3s state |
 |
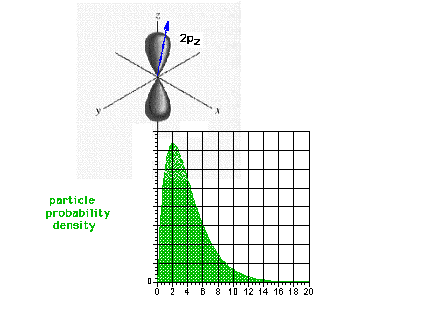
| The square of the 2pz wave function or the
probability density of the electron in a 2pz
state. |
 |
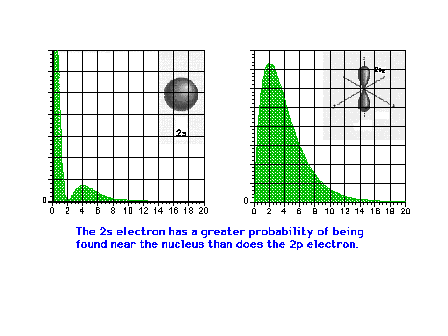
| A comparison of the electron density distribution for
the 2s and 2p waves. The 2s has a larger average radius
than the 2p, but also a greater probability of being
found close to the nucleus. |
 |
| Shape and size of all the hydrogen 2p contours |
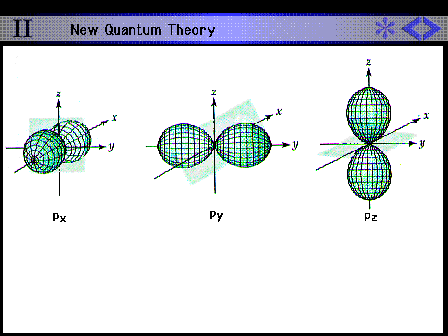 |
Shape and size of all the hydrogen 3d contours.
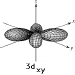
|
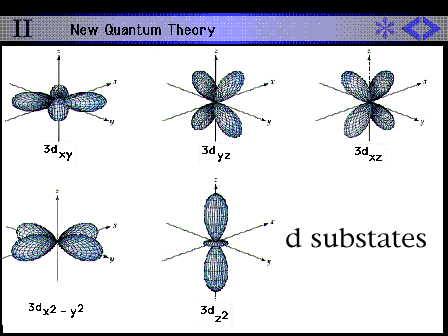 |
| Briefly...what is quantum mechanics? |
 |
| The Uncertainty Principle is an inherent part of
wave-particle duality |
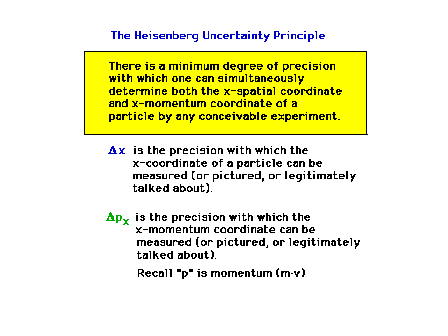 |
| The Uncertainty Principle (Section 12.5) |
 |
| An example calculation showing how location in space
and knowledge of momentum are intertwined through
wave-particle duality and the Uncertainty Principle |
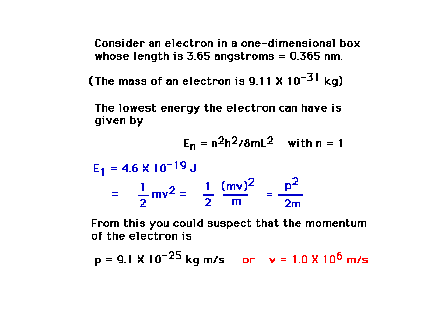 |
| Conclusion of the calculation showing a 16%
uncertainty in momentum is unavoidable |
 |
| A calculation exploring whether or not we can improve
our knowledge by using a higher resolution probe of
geometry. The uncertainty in momentum is seriously worse
than before. (The spread in velocities is about 3 million
m/s compared to the average of 1 million m/s) |
 |
| With wave-particle duality, the
description of where a particle is moving -- its pathway
through space -- is meaningless. (Absolutely meaningless
in the realm where wavelengths are comparable to the size
of the system, like atoms and molecules, but unlike
baseball) We know only the region of space in which the
particle is probably found. We are obligated to
talk about probabilities. The concept of orbits, like
Bohr's planetary paths, are replaced with wave
"orbitals". The word orbitals is used
to mean the wave that describes a bound particle. |
 |
| The probability density measures
what fraction of the "electron" is found in a
cubical volume element around a particular point (x,y,z)
with respect to the nucleus. |
 |
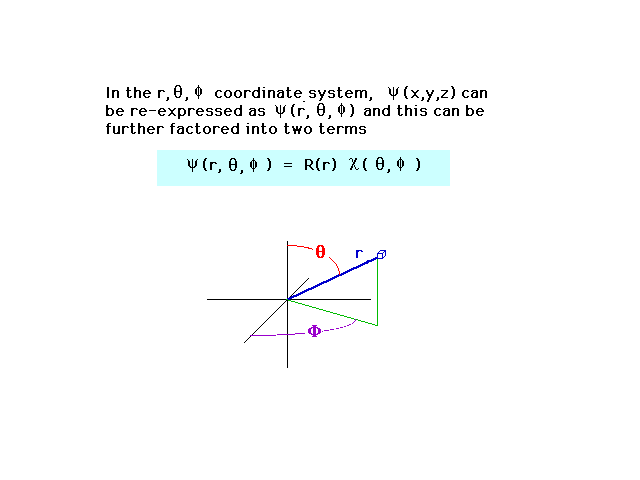
| We can also write the wave amplitude in
spherical coordinates. For a central nucleus, the wave
ammplitude then factors into two parts, one of which
depends only on the distance r between the nucleus and
electron. (You do not need to know the
blue-striped equation.) |
 |
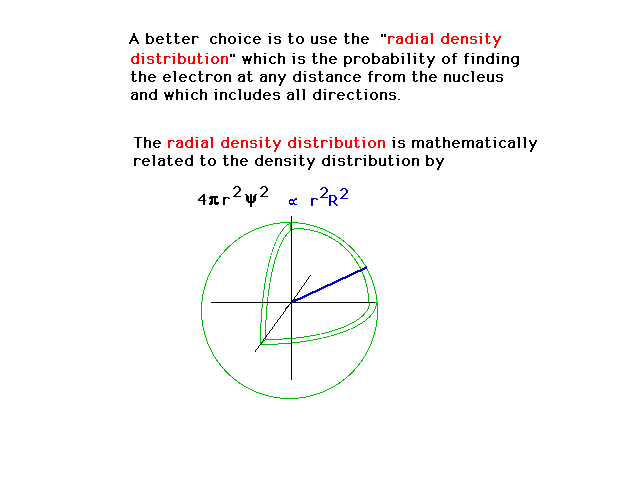
| Another way of describing the density is then
by the fraction of the electrons distribution that is in
a spherical shell volume element at distance r from the
nucleus and covering all angles. (From the previous
slide, R is that part of the wave function that depends
only on distance from the nucleus, r.) |
 |
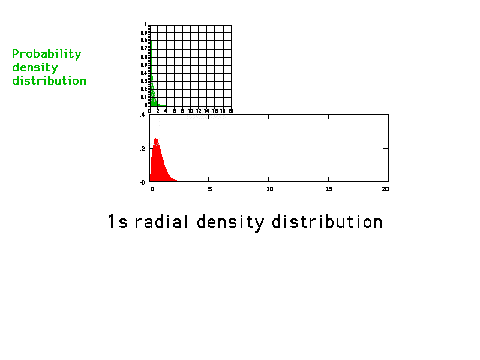
| A graphical comparison of the density
distribution (amplitude squared) and the radial
density distribution (amplitude squared multiplied by
r-squared) for a 1s orbital. The radial density
distribution graph is also referred to in the text as an
electron density plot. (p. 265) |
 |
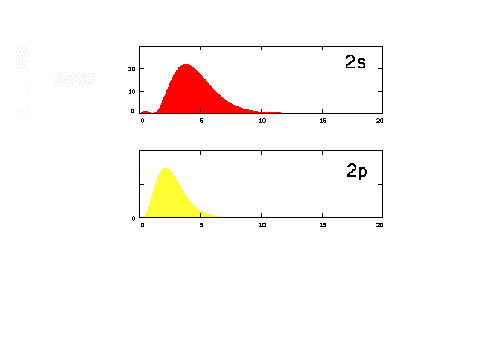
| The radial density distribution for the
n = 2 orbitals. |
 |
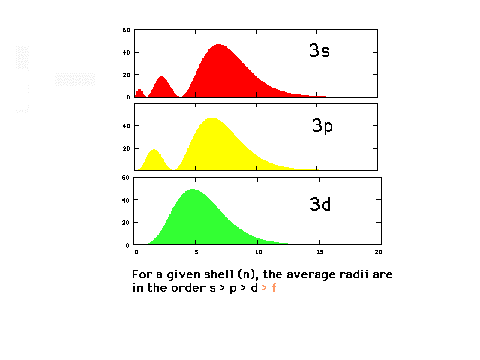
| The radial density distributions for the
n=3 orbitals. |
 |
| A close-up of the radial density
distribution near the nucleus. The blue "cloud"
represents where the inner, 1s electrons would most
likely be found. |
 |
Another mathematical consequence of wave
behavior can be expressed in a simple statement. This is
crucial as soon as we deal with more than one electron.
|
 |
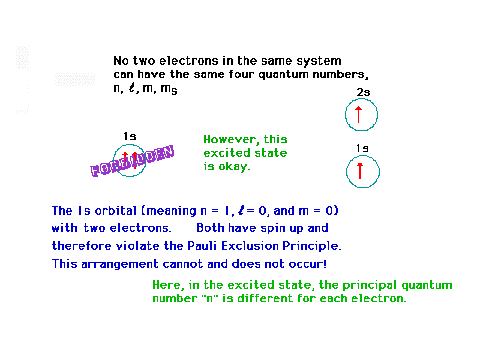
| Illustrating the Pauli Principle for two
electrons. |
 |
| Continuing with our illustratiion of two
electrons. |
 |
| More discussion on two electrons. |
 |
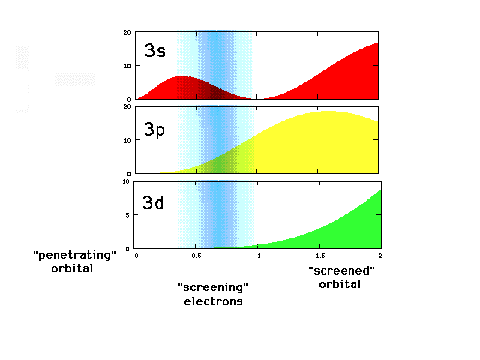
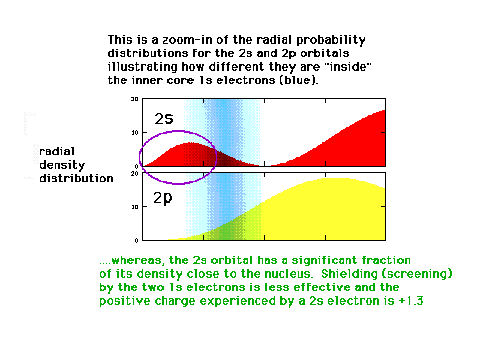
| A reminder that an electron in a 2s orbital has
a different distribution with respect to the nucleus
(origin) than when it is in the 2p orbital. |
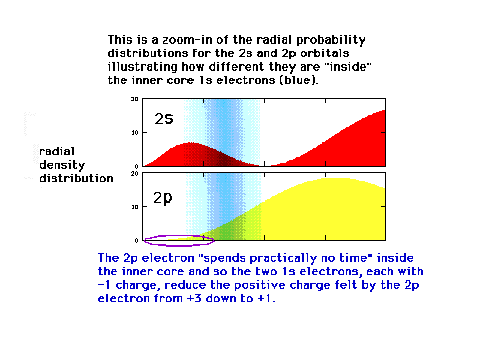 |
| A 2s electron will be attracted by a greater
net positive charge than a 2p electron because of the
different effectiveness of the screening by inner core
electrons. |
 |