Lecture #34
 
  CURMUDGEON GENERAL'S WARNING. These "slides" represent highlights from lecture and are neither complete nor meant to replace lecture. It is advised not to use these as a reliable means to replace missed lecture material. Do so at risk to healthy academic performance in 09-105.
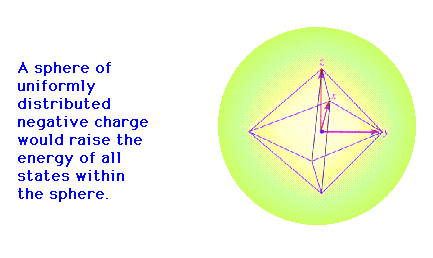
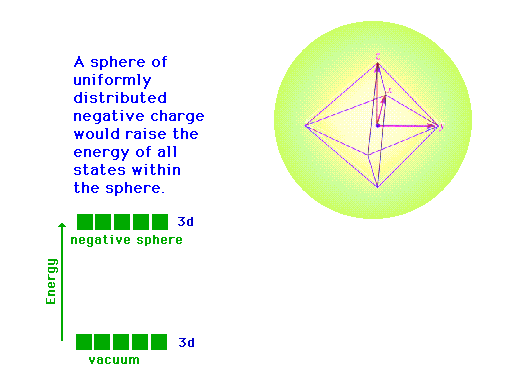
Lecture Outline Transition Metal Complexes

Crystal Field theory (Octahedral geometry)

Weak field vs strong field

Spectrochemical series

Square planar and tetrahedral geometries
Crystal field theory addresses all the "puzzles" from the previous lecture.
Developing the idea of crystal field theory..
 
Following what happens to the outer d-orbitals when a transition metal ion is placed in a spherically distributed negative charge, and then one that has octahedrally deployed negative charges.
 
 
 
 
 
The weak field splitting and strong field splitting of the d-orbitals illustrated.
You need to know the relative crystal field strengths of a restricted number of ligands indicated here.
The electron configuration in the weak field complex CoF63- and the strong field complex Co(NH3)63+.
Co3+ complex ions, their crystal field splitting energies, the color of light absorbed, and the color that the complex appears.
Leaving the discussion of coordination number = 6 (octahedral geometries) and proceeding to coordination number four.
Returning to an octahedral geometry, we look at the effect of having a weak ligand plus five stronger ligands. The weak ligand is assumed to be on the z-axis which stabilizes transition metal ion valence orbitals directed that way
Co3+ transition metal complex ions with one of the ligands varying shifts the wavelength of light absorbed to longer wavelengths as that one ligand becomes "weaker" in the field it produces.
Measured optical properties (colors) of Co3+ transition metal complex ions. What do you estimate the color of the last complex to be? This last complex is meant to be just the trans geometric isomer.
The tetrahedral crystal field geometry (without demonstrating how to generate the result) turns out to be the exact inverse orbital order of that seen in the octahedral geometry.