| Lecture
#3 |
We are now in Chapter 12 of the textbook. Many
homework problems, though, continue with drilling on
aspects of stoichiometry. |
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
| Lecture outline. |
Mass spectra (molecules) Problems
with some results of physical measurements
Line spectra
Photoelectric Effect
Blackbody Radiation (and the ultraviolet
catastrophe)
(Old Quantum Theory)
Physics puzzles "solved" by quantization
Blackbody radiation, Planck, E=hv, energy
jumps
Photoelectric Effect, Einstein, the photon
Line spectra for hydrogen
New Quantum Theory)
deBroglie and wave-particle duality of matter
|
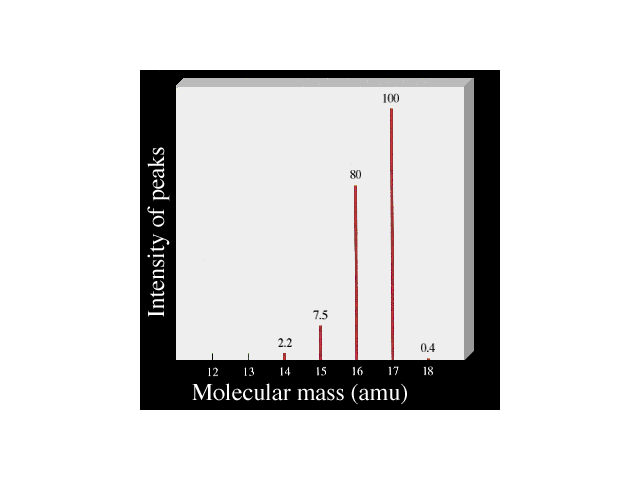
The mass spectrometer can also be used to determine
molecular ion mass/charge ratios. Here is a schematic
spectrum for ammonia, NH3. The largest peak
(at m/q = 17, intensity arbitrarily set = 100) is that
for NH3+ (mass = 14 + 1 + 1 + 1).
The peak at m/q = 16, for example, is due to a fragment,
NH2+. |
 |
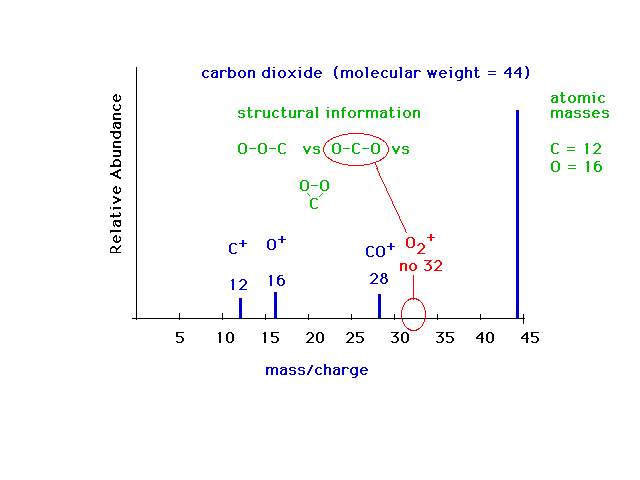
| Mass specrometry is a very valuable technique. It is
used extensively today for identifying molecules, even
quite complex ones. Here is an example of the mass
spectrum for a simple molecule, carbon dioxide,
illustrating how structural information about the intact
molecule can be obtained from the mass pattern of its
break-up fragments. Three possible bonding arrangements
are shown. In two, it would be expected that an O2+
ion would appear in the mass spectrum, but no such ion
appears. It is reasonable to conclude that the correct
arrangement is OCO. |
 |
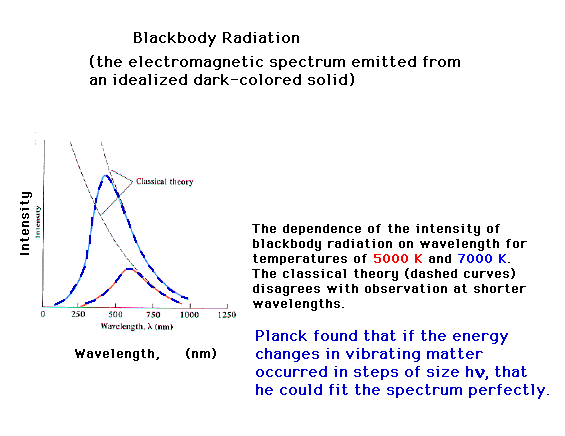
| One of the major puzzles in experimental physical
science near the end of the nineteenth century was the
spectrum of light emitted by a "body" at
different temperatures. Classical theories of physics
were extremely successful in many arenas, but for
radiation spectra predicted that intensity would vary
inversely with (l)4. (You recall what l
represents, right?)
Max Planck will propose a startling solution, that energy
takes place in discrete jumps...is quantized. For the
vibrationsin solid matter, representing "heat",
the energy is given by integral multiples of hn. Then the entire spectrum is
explained for all wavelengths, for all temperatures.
E=hn where h is now known
as Planck's constant and n is
a vibration frequency.
|
|
An explanation for the mysterious photoelectric was
totally lacking at the end of the last century. Some
colors of light could eject electrons from certain
surfaces. And if the correct colors were chosen, no
matter how dim the light, an electron could be ejected as
soon as the light struck the surface.
|
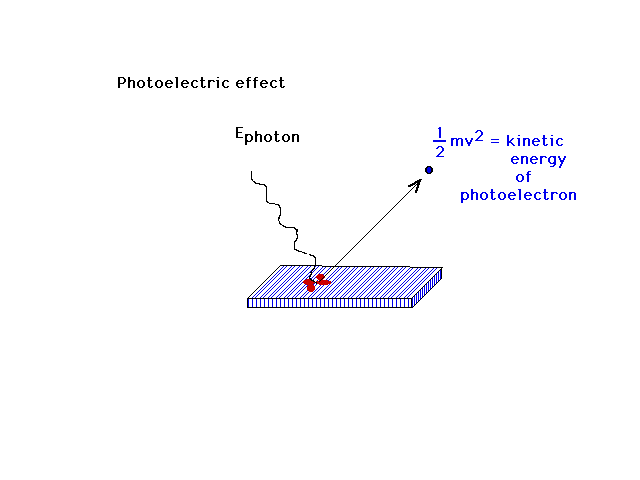 |
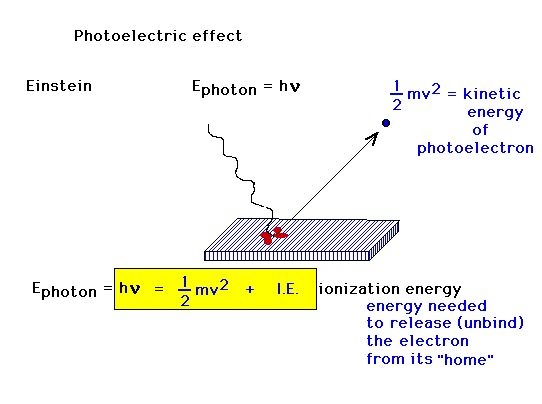
| Albert Einstein uses Planck's idea about quantization
to quantize the energy associated with light; that light
exists in discrete packets whose individual energies are
determined by their frequency. These photons are thus
able to have high enough frequencies (short enough
wavelengths) to eject photoelectrons. In contrast, they
are also thus capable of having insufficient energy if
their frequencies are too low. Conservation of energy
relates the incident "photon" energy to the
ejected photoelectron kinetic energy as highlighted here. |
 |
| Early attempts at explaining some serious puzzles in
physics established what is now referred to as "old
quantum theory". |
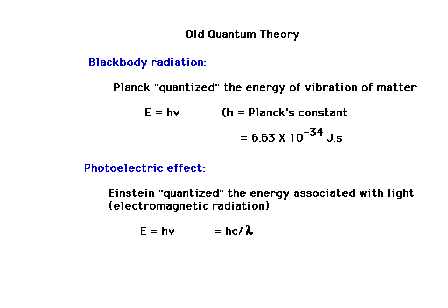 |
| The hydrogen line spectra frequencies were
consolidated by Rydberg into a single equation involving
integers. |
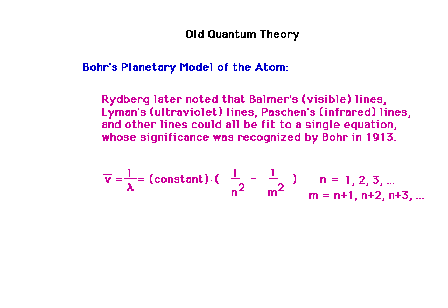 |
| Bohr's derivation of his planetary model involved an
"arbitrary quantization" of angular momentum. |
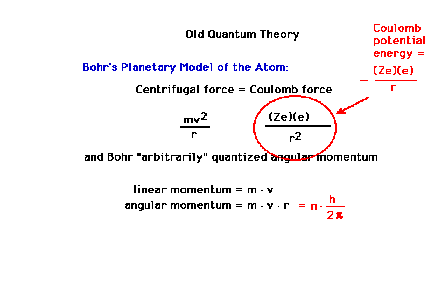 |
| Bohr's derivation led to prediction of discrete
orbital radii for an electron moving about a nucleus and
also for discrete energies that the electron was
permitted to have. |
 |
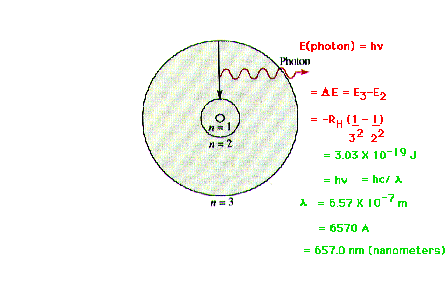
| Illustrating the transition from shell 3 to shell 2
in Bohr's planetary model. The energy difference shows up
as the energy associated with a quantum of
electromagnetic radiation; that is, a photon |
 |
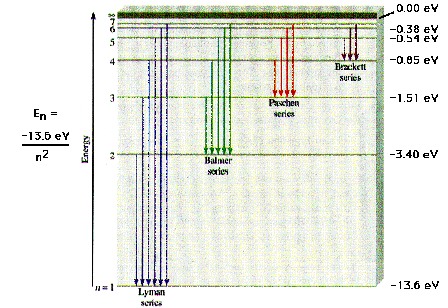
| The transitions between levels as observed in spectra
and as predicted by Bohr's model for the hydrogen atom. |
 |
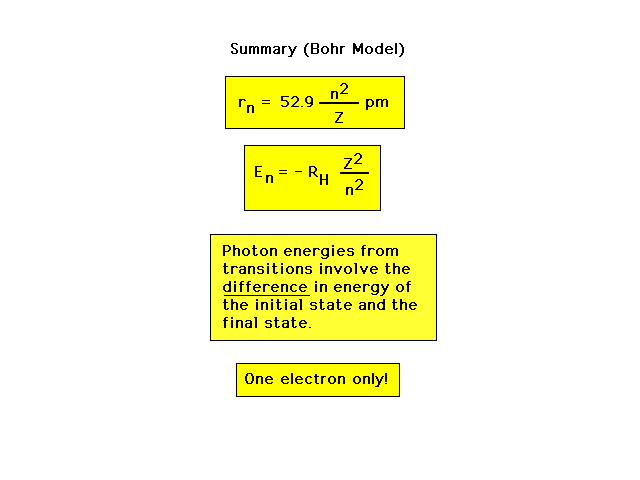
| Summary of the Bohr Planetary Model (for one
electron; old quantum theory) |
 |


