| Lecture
#23 |
Chapter 5
|
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
Lecture Outline
|
Intermolecular Interactions
Ideal gases
Real gases (Van der Waals)
- Excluded volume effect
- Intermolecular attractions
|
| Behavior of collections of molecules depends on
intermolecular interactions, which we now begin to
explore. |
 |
| The "ideal gas" is defined. It has no
intermolecular interactions. |
 |
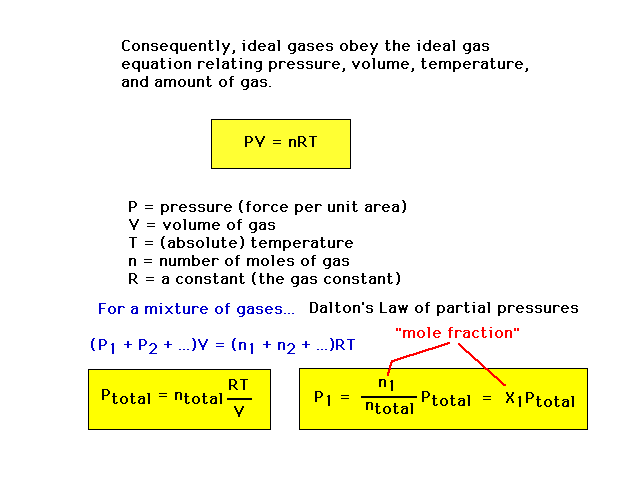
| The "ideal gas equation" relating
measurable properties of an ideal gas. |
 |
| The ease with which a gas can be compressed is
measured through its "compressibility", defined
here. |
 |
| Continued discussion about the ease with which a gas
can be compressed to smaller and smaller volumes. |
 |
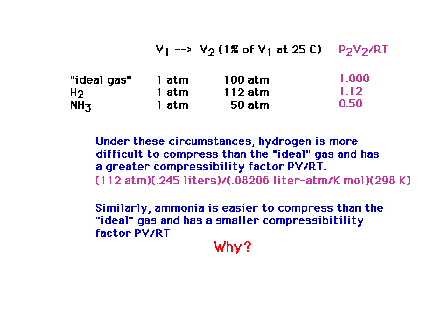
| Sample calculations of compressibilities. If H2
and NH3 were ideal, their compressibilities
would have been unity (1.0000). |
 |
| A brief table of compressibilities. |
 |
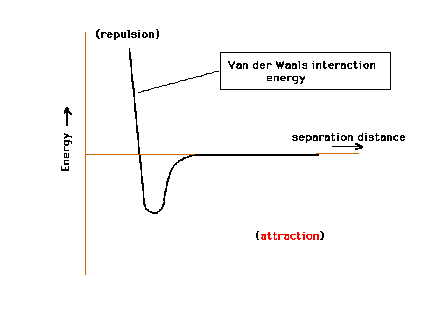
| The Van der Waals interaction between two molecules.
At large distances, there is no interaction (E=0). At
close distances, the interaction is repulsive: the
molecules cannot get too close without having to add
energy to the system. At intermediate distance there is a
range of separations where the interaction is attractive. |
 |
| Van der Waals recognizes that a volume, equivalent to
that occupied by the gas molecules themselves, is
excluded from the space over which molecules can move. |
 |
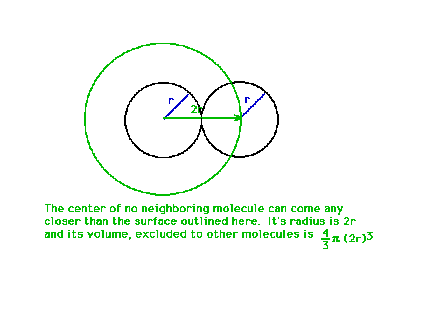
| The excluded volume for a molecule is calculated from
the molecule's geometric characteristics -- here just the
radius. |
 |
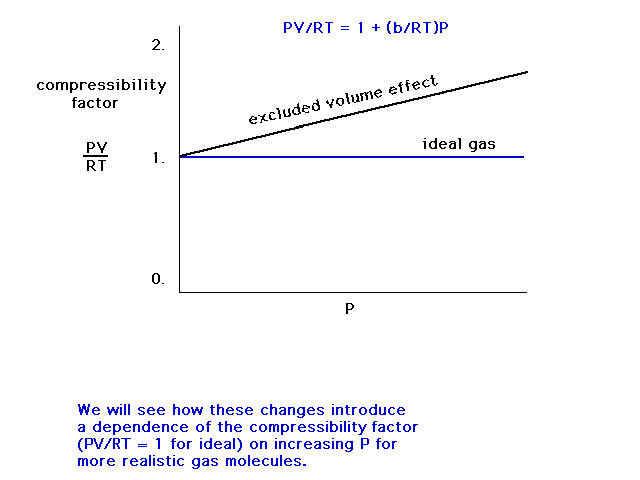
| The compressibility of a gas whose molecules have
size varies linearly with pressure, P. |
 |
| A graph of the compressibility (PV/RT) of a gas which
interacts through a repulsive force (has size). |
 |
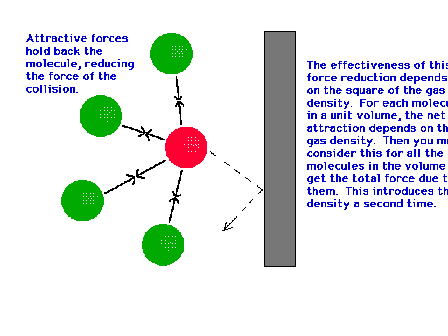
| Besides repulsive interactions at short ranges
associated with the excluded volume "b", we
have attractive interactions at distances somewhat
greater than the contact distance between molecules. |
 |
| For real gas molecules, the attractions due to
neighboring molecules retards the velocity of the
collisions at the walls, reducing the pressure expected
for ideal gases (where there are no such interactions). |
 |
| The ideal pressure would be equal to the measured
pressure plus a correction factor to account for
the reduction by attractive molecule-molecule forces. |
 |
| The gas compressibility, PV/RT, when the size effect
("b") is ignored, can be approximated by a
linear relationship, varying with P with a negative
slope. |
 |
| A graph of the compressibility of a gas in which
there are attractive, intermolecular forces (and in which
the excluded volume effect is ignored). |
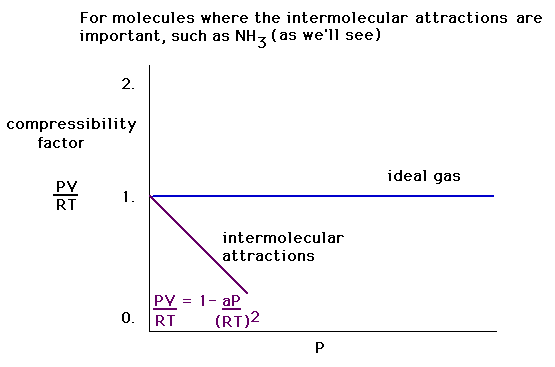 |
| The combined intermolecular forces produce a
compressibility dependence on pressure that looks like
this. |
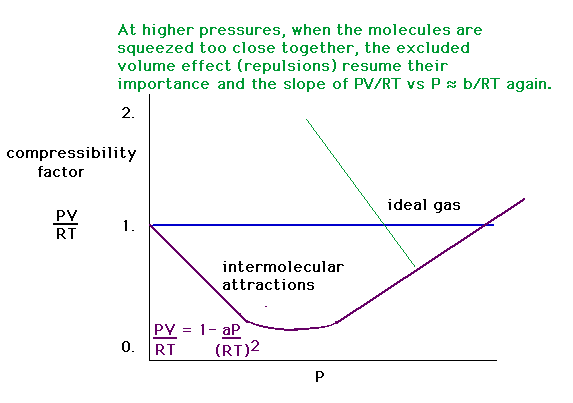 |
| The "van der Waals" equation for real gas
behavior has treated the excluded volume repulsion and
intermolecular attraction separately and introduces the
correction from each separately into the "V"
and "P" terms of the ideal gas equation. You do
not need to know the van der Waals equation. Even the
text has this as an unnumbered equation (p. 210). |
 |
| Behavior of some common real gases as a function of
pressure. |
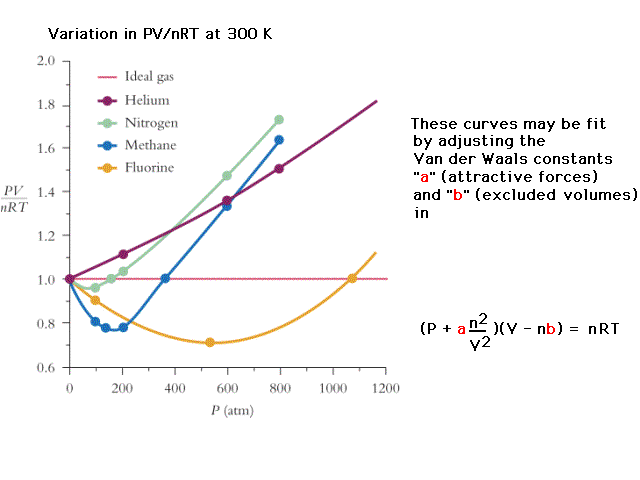 |
| Behavior of nitrogen as a function of pressure at
three different temperatures. |
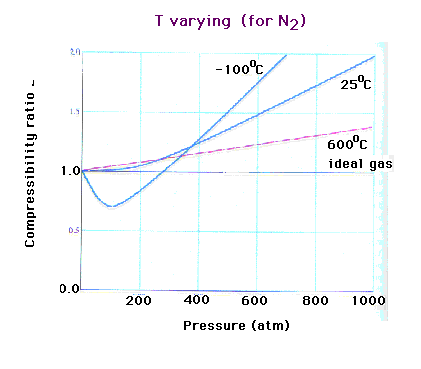 |
| Typical parameters of the van der Waals real gas
equation. Their relationship to structure will be
discussed. |
 |