| Lecture
#26 |
| Text: Chapter 5, sections 1-5, 10, 11 |
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
| |
Intermolecular Interactions
Ideal gases
|
| Behavior of collections of molecules depends on
intermolecular interactions, which we now begin to
explore. |
 |
| The "ideal gas" is defined. It has no
intermolecular interactions. |
 |
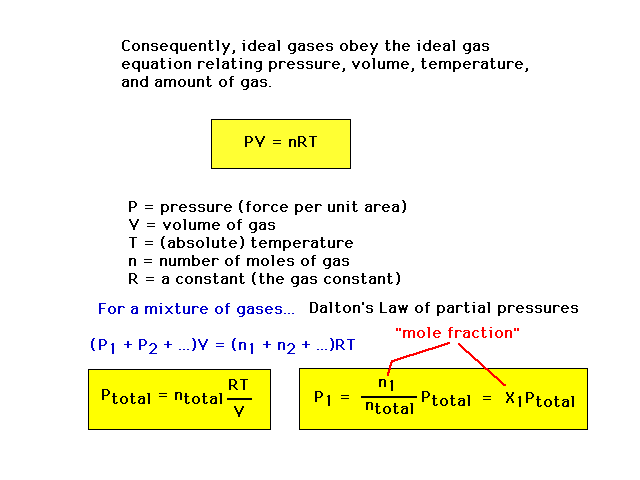
| The "ideal gas equation" relating
measurable properties of an ideal gas. |
 |
| The ease with which a gas can be compressed is
measured through its "compressibility", defined
here. |
 |
| Continued discussion about the ease with which a gas
can be compressed to smaller and smaller volumes. |
 |
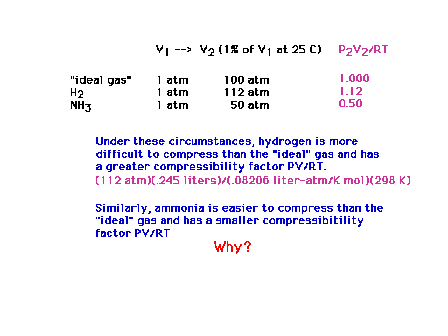
| Sample calculations of compressibilities. If H2
and NH3 were ideal, their compressibilities
would have been unity (1.0000). |
 |
| A brief table of compressibilities. |
 |
| Ideal gases have no size, something which is
unrealistic. One correction factor to gas behavior is the
non-zero size effect or "excluded volume"
effect. |
 |
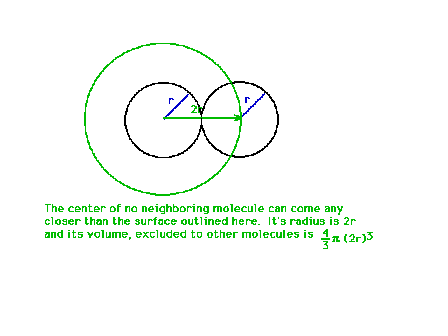
| Around each molecule there can be visualized a region
inside of which no neighboring molecule can approach. |
 |
| The excluded volume correction is applied very simply
to the ideal gas behavior. |
 |
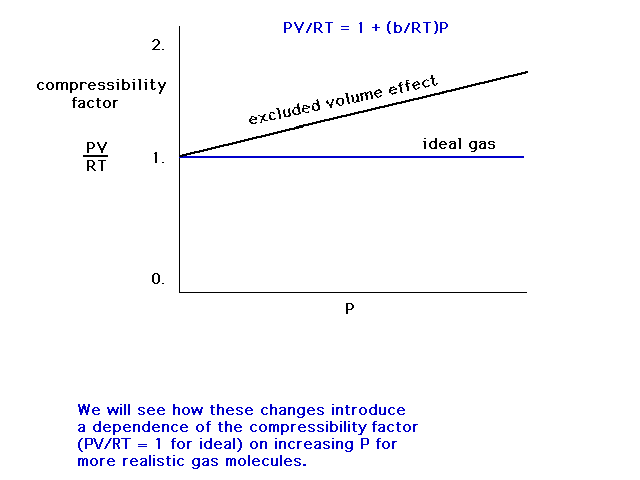
| Compressibility depends on molecular size. |
 |
| Besides repulsive interactions at short ranges
associated with the excluded volume "b", we
have attractive interactions at distances somewhat
greater than the contact distance between molecules. |
 |
| For real gas molecules, the attractions due to
neighboring molecules retards the velocity of the
collisions at the walls, reducing the pressure expected
for ideal gases (where there are no such interactions). |
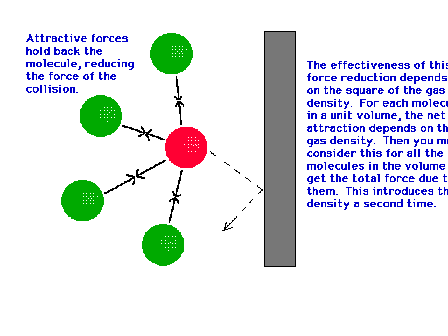 |
| The ideal pressure would be equal to the measured
pressure plus a correction factor to account for
the reduction by attractive molecule-molecule forces. |
 |
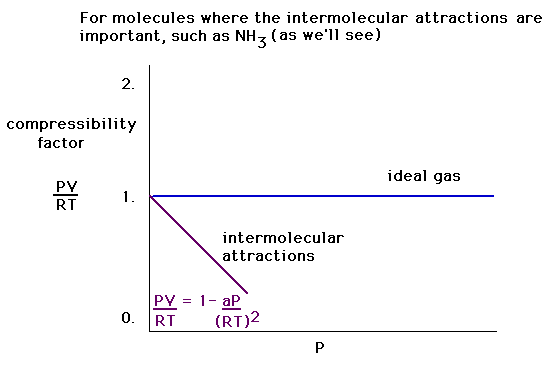
| The gas compressibility, PV/RT, when the size effect
("b") is ignored, can be approximated by a
linear relationship, varying with P with a negative
slope. |
 |
| A graph of the compressibility of a gas in which
there are attractive, intermolecular forces (and in which
the excluded volume effect is ignored). |
 |
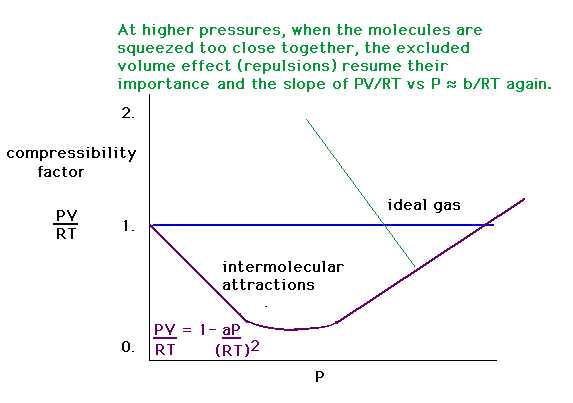
| The combined intermolecular forces produce a
compressibility dependence on pressure that looks like
this. |
 |
| The "van der Waals" equation for real gas
behavior has treated the excluded volume repulsion and
intermolecular attraction separately and introduces the
correction from each separately into the "V"
and "P" terms of the ideal gas equation. You do
not need to know the van der Waals equation. |
 |